
3-й семестр / Лекции / 13 - презентация
.pdf
Лекция 13
4. Ряды с комплексными членами. Ряды Тейлора и Лорана
4.2. Ряд Лорана, его область сходимости 4.3. Примеры разложения функций в ряд Лорана
|
|
|
4.2. Ряд Лорана, его область сходимости |
|||||||||
Определение 6. Рядом Лорана называется ряд вида |
|
|
||||||||||
… + (− |
|
) + + − |
+ 0 + 1( − 0) + 2( − 0)2 + + |
|||||||||
|
|
− |
|
|
−1 |
|
|
|
|
|
|
|
|
|
0 |
0 |
|
|
|
− |
|
|
|||
( − |
) + = ∑∞ |
|
( − |
) + ∑∞ |
|
, |
||||||
|
) |
|||||||||||
|
0 |
|
|
|
=0 |
0 |
=1 (− |
|
||||
|
|
|
|
|
|
|
|
|
|
0 |
|
|
где |
, |
|
– комплексные постоянные, а – комплексная |
|||||||||
0 |
|
|
|
|
|
|
|
|
|
|
|
|
переменная.
Областью сходимости ряда Лорана является общая часть областей
сходимости рядов: ∑∞ |
|
( − |
) и ∑∞ |
− |
|
|
) |
||||
=0 |
|
0 |
=1 (− |
||
|
|
|
|
0 |
|
Областью сходимости первого ряда является внутренность круга
| − 0| |
< . |
|
|
|
|
|
|
|
|
|
||
Найдем |
область сходимости ряда |
∑∞ |
− |
|
, |
сделав |
замену |
|||||
|
) |
|||||||||||
|
|
|
|
=1 (− |
|
|
|
|
|
|||
|
1 |
|
|
0 |
|
|
|
|
1 |
|
||
= |
. Полученный ряд ∑=0∞ |
− сходится |
в круге |
| | < |
, |
|||||||
− 0 |
|
|||||||||||
|
|
|
|
|
|
|
|
|
|
|||
следовательно, рассматриваемый ряд сходится в области | − 0| > .
Если < , областью сходимости ряда Лорана является кольцо
< | − 0| < . Здесь ≥ 0, 0 ≤ ≤ +∞.
Теорема 4. Функция ( ), однозначная и аналитическая в кольце
< | − 0| < (не исключаются случаи = 0 и = +∞),
разлагается в этом кольце единственным образом в сходящийся к ней ряд Лорана
( ) = |
∑∞ |
( − |
) = ∑−1 |
|
( − |
) + ∑∞ |
|
( − |
||||||
0) , |
|
|
=−∞ |
|
0 |
=−∞ |
|
0 |
=0 |
|
|
|||
|
|
|
|
|
|
|
|
|
|
|
|
|
||
где коэффициенты находятся по формулам |
|
|
||||||||||||
|
|
1 |
|
|
( ) ( |
|
|
) |
|
|
|
|
||
|
|
|
|
|
|
|
|
|
|
|||||
|
= |
|
|
|
|
|
|
= 0, ±1, ±2, . . . . |
|
|
|
|||
2 ∫ (− )+1 |
|
|
|
|||||||||||
|
|
|
|
|
|
|
|
|
||||||
|
|
|
|
|
|
0 |
|
|
|
|
|
|
|
|
Здесь |
– произвольная окружность с центром в точке 0, лежащей |
||||
внутри данного кольца. |
|||||
Ряд |
∑∞ |
|
( − ) называется правильной частью ряда Лорана, а |
||
|
=0 |
|
0 |
||
ряд |
∑∞ |
|
− |
|
называется главной частью ряда Лорана. |
|
|
) |
|||
|
=1 (− |
|
|||
|
|
0 |
|
|
|
Замечание. Так как кольцо является областью аналитичности функции ( ), то на границах кольца имеется хотя бы по одной точке, в которой аналитичность функции нарушается.
На практике при нахождении коэффициентов используют готовые разложения в ряд Тейлора элементарных функций.
4.3. Примеры разложения функций в ряд Лорана
Пример 1. Разложить в ряд Лорана функцию |
|
|
= |
− 2 |
|
|
1 |
||||||||||||
|
|
|
|
|
|
|
|
|
|
|
( |
) |
|
( |
) |
|
|
||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
3 −2 |
||
в окрестности точки 0 = 2. |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||
1 |
|
|
( ) |
= |
1 |
|
. |
|
|
|
|
|
|
|
|
|
|||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||
Сделаем замену = −2, получим |
|
3 |
|
|
|
|
|
|
|
|
|
||||||||
= 1 + + |
2 |
|
|
|
|
|
∞ |
|
|
|
|
|
|
|
|||||
|
+. . . + |
|
|
+. . . = ∑ |
|
|
|
|
|
|
|
|
|
||||||
2! |
! |
|
! |
|
|
|
|
|
|||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||
=0
Тогда
( ) |
( |
)3 |
|
|
1 |
|
|
|
|
|
|
|
|
1 |
|
|
|
|
|
|
|
|
1 |
|
|
|
|
1 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||
(1 + |
|
|
+ |
|
|
( |
|
|
)2 + |
|
|
|
|
( |
)3 |
+ |
|
|
( |
)4 + |
||||||||||||
|
= − 2 |
− 2 |
|
|
|
|
3! |
|
4! |
|||||||||||||||||||||||
|
|
|
|
|
|
|
2! − 2 |
|
|
|
|
− 2 |
|
− 2 |
|
|
|
|||||||||||||||
+. . . ) = ( − 2)3 + ( − 2)2 + |
1 |
|
( − 2) + |
|
1 |
|
|
+ |
1 |
|
|
+. . . |
|
|
|
|||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||||||||||||
2! |
|
3! |
|
4! ( − 2) |
|
|
|
|||||||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
1 |
|
|
|
|
|
|
1 |
|
|
|
∞ |
|
|
|
1 |
|
|
|
|||
|
( |
)3 |
( |
)2 |
|
|
|
( |
) |
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||||
|
+ |
|
|
|
|
|
|
|
|
|
+ ∑ ( |
|
|
|
) |
|
|
|
||||||||||||||
|
= − 2 |
|
+ − 2 |
|
2! |
− 2 + |
3! |
|
|
|
|
|
||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
+ 3 |
! ( − 2) |
||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
=1 |
|
|
|
|
|
|
|
|
Это разложение справедливо для любой точки ≠ 2, т.е. в кольце
0 < |
| |
− 2 < +∞. Здесь = 0, = +∞. |
||||||
|
| |
|
|
– аналитическая. |
||||
В указанной области |
) |
|||||||
|
|
|
( |
|
|
|
|
|
Пример 2. Получить |
все |
|
разложения в ряд Лорана по степеням |
|||||
( 0 |
= 0) функции ( ) |
= |
|
2 +1 |
||||
|
|
. |
||||||
|
2+ −2 |
|||||||
Определим области аналитичности функции, приравняв знаменатель дроби к нулю: 2 + − 2 = ( + 2)( − 1) = 0, отсюда 1 = −2,
2 = 1. Изобразим на комплексной плоскости возможные области.
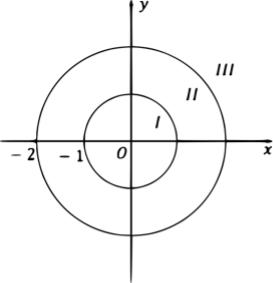
Для этого проведем окружности с центром в 0 = 0 и радиусом равным расстоянию до ближайшей особой точки. Имеем три «кольца» с центром в точке 0 = 0, в каждом из которых ( ) является аналитической:
1)круг | | < 1,
2)кольцо 1 < | | < 2,
3) 2 < | | < +∞ – внешность круга | | ≤ 2 .
Найдем ряды Лорана для функции ( ) в каждой из этих областей.
Для этого представим |
|
) |
в виде суммы элементарных дробей |
||||||||||
|
( |
|
|
|
|
|
|
|
|
|
|||
( ) |
|
2 + 1 |
|
|
|
|
|
1 |
1 |
|
|||
|
|
|
|
|
|
|
|
|
|
|
|
||
= 2 + − 2 |
= + 2 + − 1 = + 2 + − 1. |
||||||||||||
|
|||||||||||||
и нашли методом неопределенных коэффициентов.
1)Рассмотрим круг | | < 1. Преобразуем ( ):
( |
) |
|
1 |
1 |
|
|
|
|
1 |
|
|
|
|
|
|
|
|
||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||
= 2 |
1 + |
|
− |
1 − . |
|
|
|
|
|
||||||||||
|
|
|
|
|
|
|
|
||||||||||||
|
|
|
|
|
|
2 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
1 |
|
|
|
|
|
2 |
3 |
2 |
3 |
|
|
|
||||
( |
) |
|
|
|
|
|
|
|
|
|
|
|
( |
|
) |
|
|||
= |
|
(1 − |
|
|
|
+ |
2 − |
|
+. . . |
= |
|||||||||
|
|
2 |
2 |
|
3 −. . . ) − 1 + + |
|
+ |
|
|||||||||||
|
|
|
|
|
|
2 |
|
2 |
|
|
|
|
|
|
|||||
|
|
|
|
= |
1 |
|
− |
|
1 |
+ |
1 |
2 |
− |
1 |
3+. . . −1 − − 2 |
− 3−. . . |
|
|
||||||||||||||||||||||||||
|
|
|
|
|
4 |
|
|
|
|
|
|
|||||||||||||||||||||||||||||||||
|
|
|
|
2 |
|
|
|
|
|
|
|
|
8 |
|
|
16 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||||||
|
|
|
|
|
|
|
|
|
|
|
= − |
1 |
− |
3 |
− |
7 |
2 − |
|
15 |
3−. .. |
|
|
|
|
|
|
|
|
|
|||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
2 |
4 |
|
|
|
|
|
|
|
|
|
|
|
|||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
8 |
16 |
|
|
|
|
|
|
|
, |
|
при этом |
||||||||||||
Это разложение является рядом Тейлора функции |
( |
|
||||||||||||||||||||||||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
) |
|
|
|
|
ряд |
для |
|
функции |
|
|
|
1 |
|
= 1 + + 2+. .. |
сходится при |
| | < 1, а |
|||||||||||||||||||||||||||||||||
|
|
|
1− |
|
||||||||||||||||||||||||||||||||||||||||
1 |
|
|
|
|
|
|
2 |
|
|
|
3 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
| | < 2, т.е. |
||||||||||||
|
|
|
= 1 − |
|
|
+ |
|
|
− |
|
|
|
+. .. |
|
сходится |
при |
| |
|
| < 1 |
или |
|
|||||||||||||||||||||||
1+ |
|
|
2 |
4 |
|
8 |
|
|
2 |
|
||||||||||||||||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||||||||||||
2 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
внутри круга | | < 1 оба ряда сходятся. |
|
|
|
|
|
|
|
|
|
|
|
|
||||||||||||||||||||||||||||||||
2) |
Рассмотрим кольцо 1 < | | < 2. Ряд для функции |
|
|
1 |
|
остается |
||||||||||||||||||||||||||||||||||||||
|
|
|
||||||||||||||||||||||||||||||||||||||||||
1+ |
|
|||||||||||||||||||||||||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
2 |
|
1 |
|
сходящимся |
в |
этом |
|
|
кольце, т.е. | | < 2, а ряд |
для |
|
функции |
||||||||||||||||||||||||||||||||||||
|
|
|
|
|||||||||||||||||||||||||||||||||||||||||
|
|
|
1− |
|||||||||||||||||||||||||||||||||||||||||
расходится при |
| |
|
| |
> 1. |
Поэтому |
преобразуем |
|
|
|
|
|
|
|
|
||||||||||||||||||||||||||||||
|
|
|
следующим |
|||||||||||||||||||||||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
( |
) |
|
|
|
|
|
|
|||||
образом:
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
( |
) |
|
|
1 |
1 |
|
|
|
|
|
|
1 |
|
|
1 |
|
|
|
|
|
|
|
|
|
|
|
|||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
= |
|
|
|
|
|
+ |
|
|
|
|
|
|
|
|
|
|
|
1. |
|
|
|
|
|
|
|
|
|||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
2 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
1 + |
2 |
|
|
|
|
|
|
|
1 − |
|
|
|
|
|
|
|
|
|
||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
1 |
|
|
|
1 |
|
|
|
|
|
|
|
1 |
|
|
|
|
|
|
1 |
|
|
|
1 |
|
|
1 |
|
|
|
|
|
|
|
|
|
|
|
|||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
= |
|
|
|
(1 + |
|
|
+ |
|
|
|
|
|
+ |
|
|
+. . . ) |
|
|
|
|
|
||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
1 − |
1 |
|
|
|
|
2 |
3 |
|
|
|
|
|
|
||||||||||||||||||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||
Этот ряд сходится для | |
1 |
| < 1, т.е. при | | > 1. |
|
|
|
|
|
|
|
|
|
|
|
||||||||||||||||||||||||||||||||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
||||||||||||||||||||||||||||||||||||||||||||||||||||
|
|
|
( ) |
|
1 |
|
|
|
|
|
|
|
|
2 |
|
|
3 |
|
|
|
|
|
|
|
|
|
1 |
|
|
|
|
|
|
|
1 |
|
1 |
|
1 |
|
|
|
|||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||
|
|
|
= |
|
|
(1 − |
|
|
|
+ |
|
2 |
|
|
− |
|
3 +. . . ) + |
|
|
|
|
|
(1 + |
|
|
+ |
|
2 + |
|
3 +. . . ) = |
|||||||||||||||||||||||||||||||||
|
|
2 |
2 |
|
|
|
|
|
|
|
|||||||||||||||||||||||||||||||||||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
2 |
|
|
|
|
|
2 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||||||||||||
|
1 |
|
|
|
|
|
|
2 |
3 |
|
|
|
|
|
|
|
1 |
|
|
|
1 |
|
|
1 |
|
|
|
|
1 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||||||||
= |
|
− |
+ |
|
|
− |
|
|
+. . . + |
+ |
+ |
|
+ |
+. . . = ∑=0∞ (−1) |
|
+ |
|||||||||||||||||||||||||||||||||||||||||||||||
2 |
4 |
8 |
|
16 |
|
2 |
3 |
3 |
2+1 |
||||||||||||||||||||||||||||||||||||||||||||||||||||||
∑∞ |
|
1 |
. |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||
=0 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||
3) Рассмотрим | | > 2. Представим ( ) |
в виде |
|
|
|
|
|
|||||||||||||||||||||||||||||||||||
|
|
|
|
|
|
|
( ) |
1 |
1 |
|
|
|
1 |
1 |
|
|
|
|
|
|
|
|
|
||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||
|
|
|
|
|
|
|
= |
|
|
1 |
+ |
|
|
|
2. |
|
|
|
|
|
|||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
1 + |
|
|
|
|
|
||||||||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
1 − |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||
( |
) |
1 |
1 |
1 |
|
|
1 |
|
|
|
|
|
|
|
|
1 |
|
2 |
|
|
4 |
8 |
|
||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||
= |
(1 + + 2 |
+ 3 |
+. . . ) + (1 − + 2 − 3 +. . . ) = |
||||||||||||||||||||||||||||||||||||||
|
|
||||||||||||||||||||||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
2 |
|
|
|
|
1 |
|
|
5 |
|
7 |
|
|
|
|
|
|
|
|
|
|
|
|
||||||||
|
|
|
|
|
|
|
= |
|
|
− |
|
+ |
|
− |
|
+. .. |
|
|
|
|
|
|
|
|
|
||||||||||||||||
|
|
|
|
|
|
|
|
|
2 |
3 |
4 |
|
|
|
|
|
|
|
|
|
|||||||||||||||||||||
Первый ряд сходится при | | > 1, второй – |
при | | > 2. В кольце |
||||||||||||||||||||||||||||||||||||||||
2 < | | < +∞ сходятся оба ряда. |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||||||||||||||
Таким образом, в разных областях функция |
|
) |
представима |
||||||||||||||||||||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
( |
|
|
|
|
|
|
||||||
разными рядами.
