
3-й семестр / Лекции / 09
.pdf
ЛЕКЦИЯ 9
Тема 1. Комплексные числа и действия над ними
1.1. Алгебраическая форма комплексного числа
Определение 1.1. Комплексным числом называется выражение вида
= + ,
где и – действительные числа, – мнимая единица, определяемая условием 2 = −1.
Числа и называются соответственно действительной и мнимой частями комплексного числа и обозначаются = Re , = Im .
Такое представление комплексного числа называется алгебраической формой комплексного числа.
Комплексное число = − называется сопряженным комплексному числу = + .
Определение 1.2. Комплексные числа = + и = + считаются равными тогда и только тогда, когда = , = .
Пример 1.1.
Решить уравнение (3 + 2 ) + (2 − ) = −1 + 4 .
Решение: Выделим в левой части уравнения действительную и мнимую части:
(3 + 2 ) + (2 − ) = −1 + 4 .
Из определения равенства двух комплексных чисел получаем
3 + 2 = −1 { 2 − = 4.
Решая эту систему, находим = 1, = −2.
1.2. Геометрическое представление комплексного числа
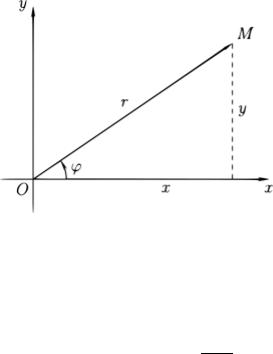
Комплексное число = + изображается на плоскости точкой с координатами ( , ), либо вектором, начало которого находится в точке
Рис. 1
(0,0), а конец в точке ( , ) (см. рис.1).
Если = 0, то = + 0 = , то есть получаем обычное вещественное, расположенное на оси , число. Если = 0, то = . Такие числа называются чисто мнимыми. Они изображаются точками на оси .
Определение 1.3. Длина вектора ( ) называется модулем
комплексного числа и обозначается |
|
|
|
||
|
|
|
|
|
(1.1) |
| | = = √2 + 2. |
|
|
|||
Определение 1.4. Угол , образованный вектором |
|
с |
осью , |
||
|
|||||
называется аргументом комплексного числа и обозначается |
= ; |
||||
определяется с точностью до слагаемого 2 ( = 0, ±1, . . . ): |
|
|
|||
= + 2 , ( = 0, ±1, ±2, . . . )
где есть главное значение , определяемое условиями − < ≤ .
В зависимости от положения точки на комплексной плоскости, |
|
|||||||||||||
|
|
|
, |
|
|
|
если z в I или IV четверти, |
|
||||||
|
|
|
|
|
|
|
||||||||
|
|
|
|
|||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
||
|
+ |
|
|
|
, |
|
если z во II четверти, |
|
||||||
|
|
|
|
|
||||||||||
|
− + |
|
, |
если z в III четверти, |
|
|||||||||
|
|
|
||||||||||||
= |
|
(1.2) |
||||||||||||
0, |
|
|
|
|
|
|
|
|
если x>0, y=0, |
|||||
|
|
|
|
|
|
|
|
|
|
|||||
|
|
|
, |
|
|
|
|
|
|
|
если x<0, y=0, |
|
||
|
|
|
|
|
|
|
|
|
|
|
|
|
||
|
|
|
|
, |
|
|
|
|
|
|
|
|
если x=0, y>0, |
|
|
2 |
|
|
|
|
|
|
|
|
|||||
|
|
− |
|
|
|
|
|
|
|
|
|
|||
[ |
|
|
, |
|
|
|
|
|
|
|
если x=0, y<0. |
|
||
2 |
|
|
|
|
|
|
|
|
||||||
Пример 1.2.
Найти модуль и аргумент комплексного числа = −1 + √3 . Решение: модуль комплексного числа вычислим по формуле (1.2)
| | = = |−1 + √3 | = √(−1)2 + (√3)2 = 2
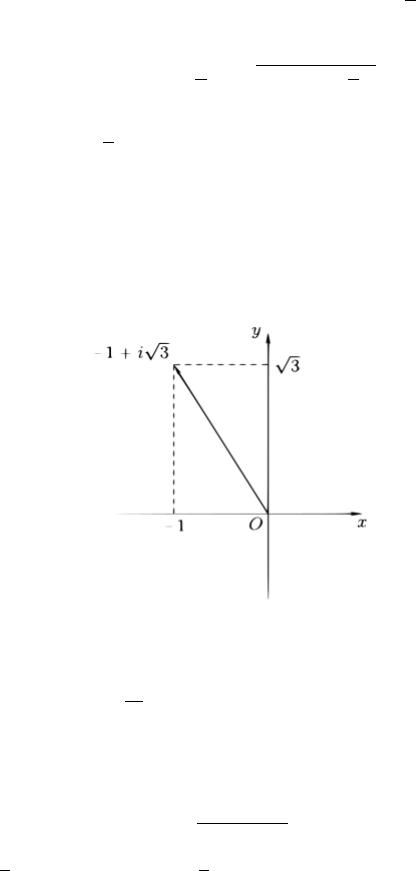
Для нахождения аргумента определим положение числа на комплексной
плоскости: = −1 + √3 лежит в II четверти. Используя формулу (1.2) найдем (см. рис. 2)
|
|
|
|
|
|
|
|
|
|
|
|
= + |
|
= + ( |
√3 |
) = |
|||||||
|
|
||||||||||
|
|
|
|
|
|
|
|
−1 |
|||
|
|
|
|
|
|
|
2 |
||||
= − √3 = − |
|
= |
|
. |
|
|
|
||||
3 |
3 |
|
|
|
|||||||
Рис. 2
Отметим, что = 23 + 2 ( = 0, ±1, ±2, . . . )
Пример 1.3.
Найти модуль и аргумент комплексного числа = −5 .
Решение: число = −5 находится на мнимой оси: = 0, = −5 < 0.
Модуль по формуле (1.1) | | = √02 + (−5)2 = 5.
= − 2 из (1.2), т. е. = − 2 + 2 ( = 0, ±1, ±2, . . . ).

1.3.Действия над комплексными числами (сложение, вычитание, умножение и деление).
Пусть даны два комплексных числа 1 = 1 + 1, 2 = 2 + 2.
Определение 1.5. Суммой + комплексных чисел и называется комплексное число
1 + 2 = ( 1 + 2) + ( 1 + 2).
Определение 1.6. Разностью − комплексных чисел и называется комплексное число
1 − 2 = ( 1 − 2) + ( 1 − 2).\
Определение 1.7. Произведением комплексных чисел и называется комплексное число
1 2 = ( 1 2 − 1 2) + ( 1 2 + 2 1).
Определение 1.8. Частным от деления комплексного
числа на комплексное число ≠ называется такое комплексное число, которое удовлетворяет уравнению = .
Для частного имеет место формула
|
1 |
|
1 |
|
|
|
1 2 + 1 2 |
|
|
2 1 − 1 2 |
|
||
|
= |
2 |
= |
+ |
. |
||||||||
|
|
| |2 |
2 |
+ 2 |
2 |
+ 2 |
|||||||
2 |
2 |
|
|
2 |
2 |
|
2 |
2 |
|
||||
Пример 1.4. Вычислить (3 − )(2 + 5 ). |
|
|
|
|
|||||||||
Решение: раскрывая скобки и учитывая 2 = −1, получим |
|||||||||||||
(3 − )(2 + 5 ) = 6 + 15 − 2 − 5 2 |
= 6 + 5 + 13 = 11 + 13 . |
||||||||||||
Пример 1.5. |
|
|
|
|
|
|
|
|
|
|
|
|
|
Вычислить −2−31+4 .
Решение: умножим числитель и знаменатель дроби на число, сопряженное знаменателю 1 − 4 .
−2 − 3 |
|
1 − 4 |
= |
−2 − 12 − 3 + 8 |
= |
−14 + 5 |
= − |
14 |
+ |
5 |
|
. |
|
|
|
|
|
|
|
||||||
1 + 4 |
1 − 4 |
1 + 16 |
17 |
17 |
17 |
|||||||
Пример 1.6. Вычислить 27.
Решение: так как
1 |
= , |
5 |
= , |
2 |
= −1, |
6 |
= −1, |
3 |
= −, |
7 |
= −, |
|
4 |
= 1, |
8 |
= 1 |
|
и т. д., то 27 = (4)6 3 = 1 (− ) = − . |
|
|||
1.4. Тригонометрическая форма комплексного числа. |
|
|||
Любое комплексное число = + ( ≠ 0) можно |
записать в |
|||
тригонометрической форме (см. рис. 1) |
|
|||
|
|
|
= ( + ), |
(1.3) |
где = | |, = . |
|
|
||
Пример 1.7.
Записать в тригонометрической форме = −√3 − . Решение: модуль найдем по формуле (1.1)
| | = = √(−√3)2 + (−1)2 = 2.
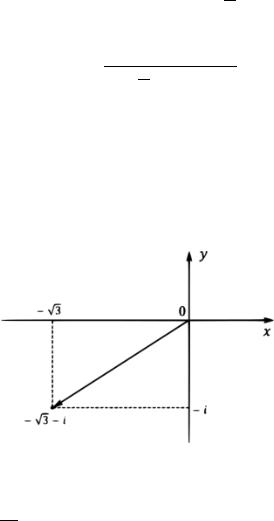
Для нахождения аргумента определим положение на комплексной плоскости: лежит в III четверти (см. рис.3), тогда по (1.2)
= − + |
−1 |
= − + |
1 |
|
= − + |
|
= − |
5 |
. |
|||
|
|
|
|
|
|
|
||||||
−√3 |
|
√3 |
|
6 |
|
6 |
|
|||||
|
|
|
|
|
||||||||
Рис. 3
Тогда = = − 56 . Подставляя значения модуля и аргумента в формулу (1.3), получим
|
|
|
5 |
|
5 |
|||
= −√3 − = 2 [ (− |
) + (− |
|||||||
|
|
|
)] |
|||||
6 |
|
6 |
||||||
1.5. Действия над комплексными |
числами, |
|
заданными в |
|||||
тригонометрической форме.
Пусть комплексные числа 1 и 2 даны в тригонометрической форме
1 = 1(1 + 1), 2 = 2(2 + 2).
1. Произведение 1 2 комплексных чисел 1 и 2 находится по формуле
1 2 = 1 2[ (1 + 2) + (1 + 2)],
т. е. при умножении комплексных чисел их модули перемножаются, а аргументы складываются
| 1 2| = | 1||2|, (1 2) = 1 + 2.
2. Частное двух комплексных чисел 1 и 2 ≠ 0 находится по формуле
|
1 |
= |
1 |
|
[ ( |
− |
|
) + ( |
− |
|
)], |
||||||
|
|
|
2 |
|
|||||||||||||
|
2 |
|
|
|
2 |
1 |
|
|
|
1 |
2 |
|
|||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||
|
| |
1 |
| = |
|
| 1| |
, |
1 |
= |
− . |
||||||||
|
|
|
|
||||||||||||||
|
|
|
2 |
|
| 2| |
|
2 |
|
1 |
|
|
2 |
|||||
|
|
|
|
|
|
|
|
|
|
|
|||||||
3. Возведение комплексного числа = ( + ) в натуральную |
|||||||||||||||||
степень производится по формуле |
|
|
|
|
|
|
|||||||||||
|
|
|
|
|
|
|
|
= ( + ), |
|
(1.4) |
|||||||
Часто формулу (1.4) также называют формулой Муавра.
4. Корень n-й степени из комплексного числа ≠ 0 имеет различных значений, которые находятся по формуле
|
|
|
|
|
+ 2 |
|
+ 2 |
|
(1.5) |
|
√ = √ ( |
|
+ |
|
), |
||||||
|
|
|||||||||
|
|
|
|
|
|
|
|
|||
где = , = 0,1,2, . . . , − 1.
Пример 1.8. Вычислить (2 − 2 )10.
Решение: представим число |
= 2 − 2 |
в тригонометрической форме: |
|||||||||||||||||
|
|
[ (− |
|
) + (− |
|
)]. |
|
|
|
|
|
||||||||
2 − 2 = 2√2 |
|
|
|
|
|
||||||||||||||
|
|
|
|
|
|
|
|
||||||||||||
4 |
|
|
|
|
|
|
4 |
|
|
|
|
|
|
|
|||||
Применяя формулу (1.4), получим |
|
|
|
|
|
||||||||||||||
|
(2 − 2 )10 |
|
|
|
|
10 |
|
|
|
|
|
|
10 |
|
10 |
|
|||
|
|
|
|
|
|
|
|
|
|
|
|||||||||
|
|
= (2√2) |
[ (− |
|
) + (− |
|
)] = |
||||||||||||
|
|
4 |
4 |
||||||||||||||||
|
= 215 ( |
5 |
|
|
5 |
= −215 . |
|
|
|||||||||||
|
|
|
) − |
( |
|
) |
|
|
|||||||||||
|
|
2 |
2 |
|
|
||||||||||||||
|
|
|
|
4 |
|
|
|
|
|
|
|
|
|
|
|
|
|
||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||
Пример 1.9. Вычислить √−16. |
|
|
|
|
|
||||||||||||||
Решение: представим число −16 в тригонометрической форме. Число
лежит на действительной оси: < 0, = 0. |
|
|
|
|
|
|
|
|
|
|
|||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||
|−16| = √(−16)2 + 02 = 16, = . |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||||
По формуле (1.5) |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||
4 |
|
|
|
4 |
|
|
|
|
+ 2 |
|
|
+ 2 |
|
||||||||||||
|
|
|
|
|
|
|
|||||||||||||||||||
|
√−16 = √16 ( |
|
|
|
|
|
+ |
|
|
|
|
|
|
|
) = |
||||||||||
|
4 |
|
|
|
|
|
4 |
||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||
|
= 2 ( |
+ 2 |
+ |
+ 2 |
) , = 0,1,2,3. |
||||||||||||||||||||
|
|
|
|
|
|
|
|||||||||||||||||||
|
|
|
|
|
4 |
|
|
|
|
4 |
|
|
|
|
|
|
|
|
|
||||||
Полагая последовательно = 0,1,2,3, выпишем все корни |
|
||||||||||||||||||||||||
|
|
|
|
= 0: 0 = 2 ( |
|
+ |
|
|
), |
|
|||||||||||||||
|
|
|
|
|
4 |
|
|||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
4 |
|
|
|
|
|
|
|
|
|||||
|
|
|
= 1: 1 |
= 2 ( |
3 |
+ |
3 |
), |
|
||||||||||||||||
|
|
|
4 |
4 |
|
|
|||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||
|
|
|
= 2: 2 |
= 2 ( |
5 |
+ |
|
5 |
), |
|
|||||||||||||||
|
|
|
4 |
4 |
|
|
|||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||
|
|
|
|
= 3: |
= 2 ( |
7 |
+ |
7 |
). |
|
|||||||||||||||
|
|
|
|
|
|
|
|||||||||||||||||||
|
|
|
|
|
3 |
|
|
|
|
4 |
|
|
|
4 |
|
|
|
|
|||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||
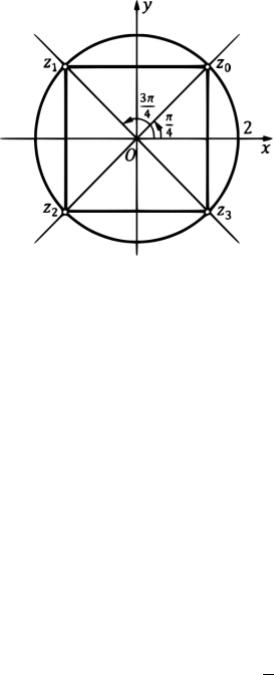
Рис. 4
На плоскости корни располагаются на окружности радиуса 2 в вершинах правильного четырехугольника, вписанного в окружность радиуса = 2 с
центром в начале координат (см. рис. 4).
Пример 1.10.
Решить уравнение 4 − 2 2 + 4 = 0. Корни уравнения изобразить на комплексной плоскости.
Решение: обозначим = 2. Тогда уравнение примет |
вид 2 − 2 + 4 = 0. |
|||||||||||||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
Корни этого уравнения 1 = 1 + √3 , |
2 = 1 − √3 , |
откуда 1,2 = √ |
|
, |
||||||||||||||||||||||||||||
1 |
||||||||||||||||||||||||||||||||
3,4 = √ |
|
. |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
2 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||
Пусть = √1 + √ |
|
|
. Найдем модуль и аргумент: |
|
|
|
|
|
|
|||||||||||||||||||||||
3 |
|
|
|
|
|
|
||||||||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
2 = 2, (1 + √3 |
) = |
. |
|||||||||||||
|
|
|
|
|1 + √3 |
| = √1 + (√3) |
|||||||||||||||||||||||||||
|
|
|
|
|
||||||||||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
3 |
|
|
|
||
Далее по формуле (1.5) получаем: |
|
|
|
|
|
|
|
|
|
|
|
|
||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||
|
|
|
|
|
|
|
( |
3 + 2 |
+ |
3 + 2 |
) , = 0,1, |
|||||||||||||||||||||
|
|
= √1 + √3 |
= √2 |
|||||||||||||||||||||||||||||
|
|
|
||||||||||||||||||||||||||||||
1,2 |
2 |
2 |
|
|
|
|
|
|
|
|||||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|||||||||||||||||||||||
т.е.
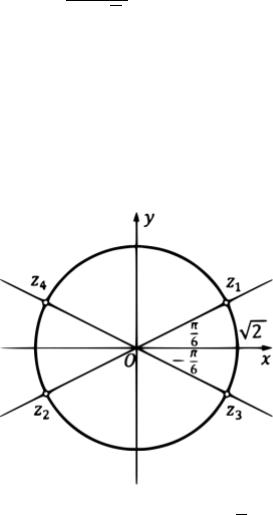
|
|
|
|
|
( |
|
|
|
|
) , = 0, |
|||||
1 |
= √2 |
|
+ |
||||||||||||
|
6 |
||||||||||||||
|
|
|
|
|
|
|
6 |
|
|
|
|
||||
|
|
|
|
7 |
|
|
|
7 |
) , = 1. |
||||||
2 |
= √2 ( |
|
+ |
||||||||||||
6 |
|
6 |
|||||||||||||
|
|
|
|
|
|
|
|
|
|
||||||
Аналогично находим = √1 − √3 .
|
|
|
|
( (− |
|
) + (− |
|
)), |
|||||
3 |
= √2 |
||||||||||||
|
|
6 |
|||||||||||
|
|
|
|
|
|
6 |
|
|
|
|
|||
|
|
|
|
5 |
) + (− |
5 |
)). |
||||||
4 |
= √2 ( (− |
||||||||||||
6 |
6 |
||||||||||||
|
|
|
|
|
|
|
|
|
|||||
Рис. 4
Все корни находятся на окружности радиуса = √2 (см. рис.5).
1.6. Показательная форма записи комплексного числа.
Используя формулу Эйлера
= +
перепишем тригонометрическую форму записи комплексного числа из формулы (1.5) в виде
= ( + ) = ,
где = | |, = , т.е. любое комплексное число ≠ 0 можно записать в показательной форме
= , = | |, = .
|
Пример 1.11. Записать комплексное число |
= −3 − 3 в |
|||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
тригонометрической и показательной форме. |
|
|
|
|
|
|
|
|
|
|
|||||||||||
|
Решение: число находится в III четверти. Найдем модуль и аргумент |
||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||
|
|
|
|
|
| | = √(−3)2 + (−3)2 = 3√2, |
|
|
|
|
|
|||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
−3 |
|
3 |
|||||
|
= − + |
|
= − + |
( |
|
) = − + |
|
= − |
|
. |
|||||||||||
|
|
−3 |
4 |
4 |
|||||||||||||||||
|
Тригонометрическая форма записи |
|
|
|
|
|
|
|
|
|
|
||||||||||
|
|
|
( (− |
3 |
) + (− |
3 |
)), |
|
|
|
|
|
|
|
|
|
|
||||
|
= 3√2 |
|
|
|
|
|
|
|
|
|
|
||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||
4 |
|
|
4 |
|
|
|
|
|
|
|
|
|
|
|
|||||||
Показательная форма записи = 3√2 −34 .
1.7. Изображение множеств на комплексной плоскости.
Изобразить на комплексной плоскости линии и области, заданные уравнениями и неравенствами.
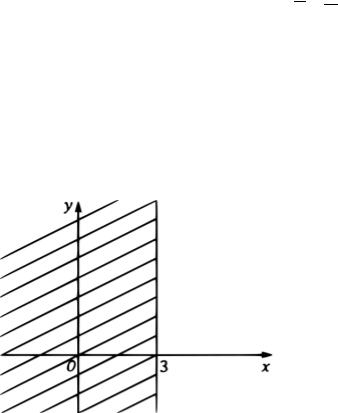
Пример 1.12. Re ≤ 3.
Решение: т.к. Re = , то неравенство можно переписать так: ≤ 3. На плоскости это определяет полуплоскость левее прямой = 3 (рис. 4).
Рис. 6
