
- •Тяжелее газ
- •Чем ниже температура (t)
- •38 Распределение Больцмана
- •51Внутренняя энергия реального газа
- •52 Эффект Джоуля-Томсона
- •60.Работа электрического поля по перемещению заряда.
- •74. Закон Ома в интегральной и дифференциальной форме
- •75. Закон Джоуля Ленца в интегральной и дифференциальной форме
- •76. Закон Ома для неоднородного участка цепи и его частные случаи
- •78.Электропроводность металлов(история)
- •80. Зависимость сопротивления металла от температуры
- •81. Затруднение классической электронной теории
- •82. Основные положения зонной теории
- •83.Разрешение трудностей классической зонной теории
- •84. Металлы, полупроводники, диэлектрики
- •85. Примесная проводимость полупроводников
- •87. Контактная разность потенциалов
- •89. Вольтамперная характеристика
№1 Предмет физики. Разделы механики. Методы физического исследования. Связь физики с другими дисциплинами. Физические модели.
Физика — это наука о природе в самом общем смысле (часть природоведения). Она изучает вещество (материю) и энергию, а также фундаментальные взаимодействия природы, управляющие движением материи. Физика связана с химией. Химические же свойства вещества однозначно определяются физическими свойствами атомов и молекул, описываемыми в таких разделах физики, как термодинамика, электромагнетизм и квантовая физика. Физика тесно связана с математикой: математика предоставляет аппарат, с помощью которого физические законы могут быть точно сформулированы. С техникой(электронная и ядерная техника). Разделы механики: Статика-изучает условия равновесия тел или их частей. Кинематика- законы движения тел без выяснения причин. Динамика- законы движения тел с учетом причин. Методы физического исследования: опыт-гипотеза-эксперимент-теория. Физическая модель надо выбирать чтобы учесть все существенные особенности поведения реального тела и пренебречь всеми второстепенными факторами. Материальная точка-тело, формой и размерами которой можно пренебречь. Абсолютно твердое тело- тело формы и размеры, которого не изменяются в условиях задачи.
№2 Элементы кинематики материальной точки. Радиус-вектор. Виды движения. Кинематические уравнения.
Элементами
кинематики являются: Перемещение-
кратчайшее расстояние от начала до
конца пути. Скорость
- определяет
быстроту движения и направление в данный
момент.
Ускорение -
физ. Величина, характеризует быстроту
изменения скорости по модулю и направлению.
радиус-вектор
— это вектор, идущий из начала координат
к исследуемой точки. Длина радиус-вектора,
или его модуль, определяет расстояние,
на котором точка находится от начала
координат, а стрелка указывает направление
на эту точку пространства. Виды
движения
можно классифицировать по разным
признакам :по величине скорости
(равномерное, переменное — ускорение,
замедленное, равноускоренное).По виду
траектории — прямолинейное, криволинейное.
Кинематические
уравнения- явный
вид функциональной зависимости координат
или радиус-вектора.
![]() .
.
![]() .
.
![]()
№3 Скорость как производная радиус-вектора. Закон независимости движений
Средняя скорость-
отношение
приращения
радиуса-вектора точки к промежутку
времени.
![]() Вектор средней скорости направлен
вдоль хорды соединяющей точки траектории.
При неограниченном уменьшении t
средняя скорость стремится к предельному
значению-мгновенной скорости.
Вектор средней скорости направлен
вдоль хорды соединяющей точки траектории.
При неограниченном уменьшении t
средняя скорость стремится к предельному
значению-мгновенной скорости.
![]() Вектор скорости ее направлен по
касательной к траектории в сторону
движения. Закон
независимости движений:
если материальная точка участвует в
нескольких движениях, то е. перемещение
равно векторной сумме перемещений, а
скорость - векторной сумме скоростей.
Вектор скорости ее направлен по
касательной к траектории в сторону
движения. Закон
независимости движений:
если материальная точка участвует в
нескольких движениях, то е. перемещение
равно векторной сумме перемещений, а
скорость - векторной сумме скоростей.
№4 Ускорение как производная радиус-вектора. Нормальное и тангенциальное ускорение
Скоpость изменения
скоpости движения точки называется
ускоpением, а точнее, ускоpение есть
пеpвая пpоизводная от скоpости точки по
вpемени или втоpая пpоизводная от
pадиуса-вектора по вpемени:
![]() Полное
ускоpение точки складывается из
касательного и ноpмального ускоpений
по пpавилу сложения вектоpов.
Полное
ускоpение точки складывается из
касательного и ноpмального ускоpений
по пpавилу сложения вектоpов.
![]() Оно всегда будет напpавлено в стоpону
вогнутости тpаектоpии, поскольку в эту
стоpону напpавлено и ноpмальное ускоpение.
Тангенциальное
ускорение
по направлению совпадает с вектором
скорости в любой точки траектории и
направлен этот вектор по касательной
к траектории. В случаи ускоренного
движения
Оно всегда будет напpавлено в стоpону
вогнутости тpаектоpии, поскольку в эту
стоpону напpавлено и ноpмальное ускоpение.
Тангенциальное
ускорение
по направлению совпадает с вектором
скорости в любой точки траектории и
направлен этот вектор по касательной
к траектории. В случаи ускоренного
движения
![]() направлено в сторону движения в случаи
замедленного движения против движения
направлено в сторону движения в случаи
замедленного движения против движения![]() Нормальное
ускорение характеризует
быстроту изменения скорости по
направлению.
Нормальное
ускорение характеризует
быстроту изменения скорости по
направлению.
![]() направлено в любой точки траектории
перпендикулярно касательной к центру
кривизны траектории в этой точки.
направлено в любой точки траектории
перпендикулярно касательной к центру
кривизны траектории в этой точки.
№5 Поступательное и вращательное движение. Кинематика вращательного движения. Угловая скорость и ускорение.
Поступательное
движение —
это движение, при котором любая прямая,
жестко связанная с движущимся телом,
перемещается параллельно сама
себе.(кабина лифта). При поступательном
движении все точки тела движутся
одинаково, поэтому достаточно изучить
движение одной какой-то произвольной
точки тела (например, движение центра
масс тела), так же при поступательном
движении тело не изменяет ни своего
вида, ни строения, одновременные скорости
всех точек равны и параллельны между
собой, также равны и параллельны между
собой ускорения всех точек. Враща́тельное
движе́ние
—движение, при котором все точки тела
движутся по окружностям, центры которых
лежат на 1 и той же прямой-ось
вращения.
Ось вращения может располагаться внутри
тела и за его пределами. Если ось вращения
проходит сквозь
тело, то
точки, лежащие на оси, при вращении тела
остаются в покое. Точки твёрдого тела,
находящиеся на
разных расстояниях от оси вращения
за одинаковые промежутки времени
проходят различные расстояния и
следовательно имеют различные линейные
скорости
Кинематика вращательного движения:
Период вращения(Т)-время,
за которое тело совершает 1 полный
оборот. Частота
вращения(![]() )-число
полных оборотов в единицу времени.
)-число
полных оборотов в единицу времени.
![]() Роль пути
во вращательном движении присуждаем
углу поворота. Угловая
скорость:
Роль пути
во вращательном движении присуждаем
углу поворота. Угловая
скорость:![]() Угловая скорость является всегда
вектором.(псевдовектор)
За направление вектора
Угловая скорость является всегда
вектором.(псевдовектор)
За направление вектора
![]() принимается направление совпадающее
с поступательным движением Буравчика.
При равномерном вращении:
принимается направление совпадающее
с поступательным движением Буравчика.
При равномерном вращении:![]() (рад/с)
(рад/с)![]() .
.
![]() в процессе вращения
можно изменять его быстроту или за счет
поворота, оси вращения. Изменение
во времени характеризуется угловым
ускорением
в процессе вращения
можно изменять его быстроту или за счет
поворота, оси вращения. Изменение
во времени характеризуется угловым
ускорением
![]() .Вектор
углового ускорения
.Вектор
углового ускорения
![]() направлен вдоль оси вращения (в сторону
направлен вдоль оси вращения (в сторону
![]() при ускоренном вращении и противоположно
— при замедленном).
при ускоренном вращении и противоположно
— при замедленном).
![]() .
.![]() .
.![]()
Вывод: Все линейные характеристики вращательного движения возрастают пропорционально от оси вращения до исследуемой точки.
№6 Связь между кинематическими характеристиками поступательного и вращательного движения
Движение тела может быть как поступательным так и вращательным. При поступательном движение любая прямая, проведенная в теле , перемещается параллельно самой себе. По форме траектории поступательное движение может быть прямолинейным и криволинейным. При поступательном движении все точки твердого тела за один и тот же промежуток времени совершают равные по величине и направлению перемещения. Следовательно, скорости и ускорения всех точек тела в любой момент времени также одинаковы. Для описания поступательного движения достаточно определить движение одной точки. Вращательным движением твёрдого тела вокруг неподвижной оси называется такое движение, при котором все точки тела движутся по окружностям, центры которых лежат на одной прямой (ось вращения)Ось вращения может проходить через тело или лежать за его пределами. Если ось вращения проходит сквозь тело, то точки, лежащие на оси, при вращении тела остаются в покое. Точки твёрдого тела, находящиеся на разных расстояниях от оси вращения за одинаковые промежутки времени проходят различные расстояния и следовательно имеют различные линейные скорости Между движением твердого тела вокруг неподвижной оси и движением отдельной материальной точки (или поступательным движением тела) существует тесная и далеко идущая аналогия. Каждой линейной величине из кинематики точки соответствует подобная величина из кинематики вращения твердого тела. Сравнительные параметры движения:
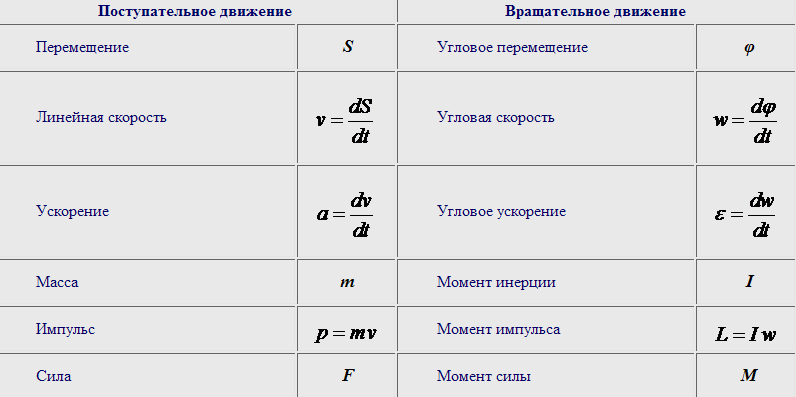
Поступательное движение можно рассматривать, как вращательное, с радиусом вращения, стремящимся к бесконечности, и угловой скоростью, стремящейся к нулю.
№7 Инерциальные системы отсчета.1 закон Ньютона. Внутренние и внешние силы. Замкнутые системы. Закон сохранения импульса.
Инерциа́льная
систе́ма отсчёта
- система отсчёта, в которых выполняется
1закон Ньютона.(солнце и
звезды),приближенные(земля и столб)Первый
закон Ньютона(закон
инерции): тело находится в состоянии
покоя или равномерного прямолинейного
движения, если на него не действуют силы
или силы скомпенсированы. Он выполняется
не всегда, только
в ИСО. Внутренние силы- силы,
с которыми части системы взаимодействуют
между собой. Внешние-силы,
с которыми части системы или она целиком
взаимодействует с телами, не входящими
в систему. Если действием внешних сил
можно пренебречь-система
замкнутая. Закон сохранения импульса:
Закон
сохранения импульсов: суммарный импульс
замкнутой системы тел сохраняется при
любых процессах внутри неё.(справедлив
только для замкнутых систем)
![]()
№8 Второй и
третий законы Ньютона
2 закон Ньютона:
ускорение, приобретаемое материальной
точкой пропорционально вызывающей его
силе, совпадает с нею по направлению и
обратно пропорционально массе материальной
точки.
![]() Общая
формулировка 2 закона Ньютона:
скорость изменения импульса мат.точки=
действующей на нее силе.
Общая
формулировка 2 закона Ньютона:
скорость изменения импульса мат.точки=
действующей на нее силе.
![]() Он
действует только в ИСО.F(H)Третий
закон Ньютона:
Тела действуют друг на друга с силами,
имеющими одинаковую природу, направленными
вдоль одной и той же прямой, равными по
модулю и противоположными по направлению:
Он
действует только в ИСО.F(H)Третий
закон Ньютона:
Тела действуют друг на друга с силами,
имеющими одинаковую природу, направленными
вдоль одной и той же прямой, равными по
модулю и противоположными по направлению:
![]() Первое
тело может действовать на второе с
некоторой силой
Первое
тело может действовать на второе с
некоторой силой
![]() ,
а второе — на первое с силой
,
а второе — на первое с силой
![]() . Он действует
только в ИСО
. Он действует
только в ИСО
№9 Центр инерции и закон его движения
Центр инерции(центр
масс) системы мат.точек-воображаемая
точка С, положение которой характеризует
распределение массы этой системы. Ее
радиус-вектор=![]()
Где mi,ri-масса и радиус-вектор i-й мат.точки. n-число мат.точек. m-масса системы.
В однородном поле(поле тяжести) центр инерции совпадает с центром тяжести.
![]() Из этого
вытекает, что
Центр
масс замкнутой системы либо движется
прямолинейно и равномерно, либо остается
неподвижным.
Из этого
вытекает, что
Центр
масс замкнутой системы либо движется
прямолинейно и равномерно, либо остается
неподвижным.
Основной закон
динамики поступательного движения
твёрдых тел:
центр инерции механической системы
движется как материальная точка, масса
которой равна массе всей системы и на
которую действует сила, равная главному
вектору внешних сил, приложенных к
системе.![]()
№10 Работа и ее выражение через криволинейный интеграл
Работа-
скалярная величина, равная произведению
проекции силы на направление перемещения,
умноженной на перемещение точки
приложения силы
![]()
Если угол
![]() -острый,
то работа считается положительной, если
-тупой,
то работа считается отрицательной если
-острый,
то работа считается положительной, если
-тупой,
то работа считается отрицательной если
![]() ,
то механическая работа не совершается
(А=0).В случаи если перемещение проходит
по криволинейной траектории или под
действием переменной силы, формула не
применима. Путь следует разбить на
прямоугольные отрезки dS,
при движении по которым сила остается
постоянной.
,
то механическая работа не совершается
(А=0).В случаи если перемещение проходит
по криволинейной траектории или под
действием переменной силы, формула не
применима. Путь следует разбить на
прямоугольные отрезки dS,
при движении по которым сила остается
постоянной.
![]()
![]()
Пример. Найти работу по растяжению пружины. Сила определяется по закону Гука.
![]()
![]() Единицей работы
является [ДЖ].
Единицей работы
является [ДЖ].
№11 Виды энергии . Потенциальная и кинетическая энергии
Кинети́ческая
эне́ргия —
энергия механической системы, зависящая
от скоростей движения её точек. Часто
выделяют кинетическую энергию
поступательного и вращательного
движения. Единица измерения в системе
СИ - Джоуль.
![]()
![]() где I-момент
инерции.
где I-момент
инерции.
Кинетическая
энергия зависит только
от массы скорости тела.
Она также зависит от выбора
системы отсчета.
Кин.энергия
механической системы
= сумме кин. Энергий тел, входящих в
систему. ∑mi*vi2/2
в пределе от i=1
до n.
Кинети́ческая
эне́ргия-всегда положительна. Потенциальная
энергия –механическая
энергия системы тел, определяемая их
взаимным расположением и характером
сил взаимодействия между ними.
Потенциальная энергия принимается
равной нулю для некоторой точки
пространства, выбор которой определяется
удобством дальнейших вычислений. Процесс
выбора данной точки называется нормировкой
потенциальной энергии. К примеру,
потенциальная энергия тела вблизи
поверхности Земли рассчитывается по
формуле
![]() , где m — масса тела, g - величина ускорения
свободного падения, h — высота, на
поверхности Земли (h = 0) величина
потенциальной энергии принимается
равной нулю.
Примеры полей, в которых можно ввести
потенциальную энергию:
поле сил всемирного тяготения,
электростатическое поле, поле сил
упругих деформаций и пр.
Потенциальная энергия может быть
отрицательна.
, где m — масса тела, g - величина ускорения
свободного падения, h — высота, на
поверхности Земли (h = 0) величина
потенциальной энергии принимается
равной нулю.
Примеры полей, в которых можно ввести
потенциальную энергию:
поле сил всемирного тяготения,
электростатическое поле, поле сил
упругих деформаций и пр.
Потенциальная энергия может быть
отрицательна.
Полная механическая энергия системы-энергия мех.движения и взаимодействия= сумме кин. и пот. энергий . Е=К+П
№12 Понятие о градиенте скалярной функции. Связь между потенциальной энергией и силой
Градиент— вектор,
показывающий направление наискорейшего
возрастания некоторой величины, значение
которой меняется от одной точки
пространства к другой. Смысл градиента
любой скалярной функции f в том, что его
скалярное произведение с бесконечно
малым вектором перемещения дает полный
дифференциал этой функции при
соответствующем изменении координат
в пространстве, на котором определена
f, то есть линейную (в случае общего
положения она же главная) часть изменения
f при смещении на
![]() .Пространство,
в котором действуют консервативные
силы, называется потенциальным полем.
Каждой точке потенциального поля
соответствует некоторое значение силы
.Пространство,
в котором действуют консервативные
силы, называется потенциальным полем.
Каждой точке потенциального поля
соответствует некоторое значение силы
![]() , действующей на тело, и некоторое
значение потенциальной энергии U.
Значит, между силой
и U должна быть связь
, действующей на тело, и некоторое
значение потенциальной энергии U.
Значит, между силой
и U должна быть связь
![]() , с другой стороны, dA = –dU, следовательно
,
, с другой стороны, dA = –dU, следовательно
,
![]() отсюда
отсюда
![]()
Вектор силы можно записать через проекции:
![]() F=-gradU
где
F=-gradU
где
![]()
Следовательно, вектор направлен в сторону наибыстрейшего уменьшения U.
№13 Закон сохранения механической энергии. Диссипация энергии. Физическое поле, поле центральных сил. Консервативные силы.
Закон сохранения механической энергии : полная механическая энергия замкнутой системы не изменяется если между частями системы действуют только консервативные силы. Если в замкнутой системе кроме консервативных сил, действуют неконсервативные силы, то полная механическая энергия даже в замкнутой не сохраняется. Таким образом, энергия никогда не исчезает и не появляется вновь, она лишь превращается из одного вида в другой-физический смысл закона. Процесс убывания механической энергии под действием неконсервативных сил называется диссипацией (рассеиванием) энергии. Все системы в природе-диссипативные. Физическое поле- особая форма материи. Оно объясняет дистанционное взаимодействие тел без контактов. Физ. поля распределяются в пространстве непрерывно. Они осуществляют взаимодействие между телами (гравитационное, электромагнитное, ядерное).Поле центральных сил-направление его силы в любую точку пространства , проходящее через общий центр. Поле, в котором работа не зависит от формы пути- потенциальное, а силы, действующие в нем- консервативные.
№14 Центральный удар шаров. Абсолютно упругий удар, Абсолютно неупругий удар (Законы сохранения)
Центральный удар-если, тела до удара движутся вдоль прямой, проходящей через их центры масс. Абсолютно упругий -механическая энергия тел не переходит в другие виды. Выполняются законы сохранения: кинетической энергии и импульса.
![]()

2. Абсолютно неупругий удар-механическая энергия после удара частично или полностью переходит в тепловую. Выполняется закон сохранения импульса. После АНУ тела объединяются в единую систему.
![]()
В проекциях запись законов сохранения импульса со знаком
"—" соответствует встречному движению и с "+" соответствует движение в одном направлении.
№15 Кинетическая энергия вращательного движения. Момент инерции тела
Рассмотрим АТТ,
вращающееся около неподвижной оси z,
проходящей через него. Мысленно разобьем
это тело на маленькие объемы с малыми
массами m1,m2…,
находящимися на расстоянии r1,r2…При
вращении твердого тела относительно
неподвижной оси отдельные его элементарные
объемы опишут окружности разных радиусов
и будут иметь разные линейные скорости
vi,
но т.к. у нас АТТ, то угловая скорость
вращения этих объемов одинакова.w=v1/r1=
v2/r2….Кин.энергию
вращающегося тела найдем как сумму
кин.энергий его элементарных
объемов.К=∑mi*vi^2/2
от i
до n.
А это =
![]() -кин.энергия
вращающегося тела .Моментом инерции
механической системы относительно
неподвижной оси a («осевой момент
инерции») называется физическая величина
Ja, равная сумме произведений масс всех
n материальных точек системы на квадраты
их расстояний до оси: (кг·м²)
-кин.энергия
вращающегося тела .Моментом инерции
механической системы относительно
неподвижной оси a («осевой момент
инерции») называется физическая величина
Ja, равная сумме произведений масс всех
n материальных точек системы на квадраты
их расстояний до оси: (кг·м²)
![]() где:mi — масса i-й
точки,ri — расстояние от i-й точки до оси.
где:mi — масса i-й
точки,ri — расстояние от i-й точки до оси.
Теорема Штейнера:
Момент инерции
данного тела относительно какой-либо
оси зависит не только от массы, формы и
размеров тела, но также от положения
тела по отношению к этой оси. Согласно
теореме
Штейнера(1)
: момент инерции тела J относительно
произвольной оси равен сумме момента
инерции этого тела Jc относительно оси,
проходящей через центр масс тела
параллельно рассматриваемой оси, и
произведения массы тела m на квадрат
расстояния d между осями:![]()
№16 Момент инерции диска Задача нахождения моментов инерции твёрдых тел сводится к интегрированию, выражения вида по элементарным массам частиц этих тел.
![]()
Найдём момент инерции однородного диска относительно оси нормальной плоскости диска и проходящей через его центр. Разобьём диск на кольцевые слои шириной dr.
![]()
Объём каждого
кольцевого слоя ![]()
![]()
№17 Момент силы, Момент импульса. Работа во вращательном движении.
Моментом силы относительно неподвижной оси называется произведение силы на плечо.
Плечо силы- кротчайшее расстояние от оси вращения до направления действия силы.
![]()
![]()
Работа
![]() ,совершаемая
при повороте стержня на угол
,совершаемая
при повороте стержня на угол ![]() может быть найдена из следующих
соображений:sin
и tg
малого угла равны самому углу
:
может быть найдена из следующих
соображений:sin
и tg
малого угла равны самому углу
:![]()
![]() Момент импульса твердого тела
относительно оси –сумма моментов
импульса отдельных частиц.L=∑mi*vi*ri
=
Момент импульса твердого тела
относительно оси –сумма моментов
импульса отдельных частиц.L=∑mi*vi*ri
=![]()
№18 Основной закон динамики вращательного движения. Закон сохранения момента импульса
Основной закон
динамики вращательного движения
относительно
неподвижной оси: производная момента
импульса твердого тела относительно
оси=моменту сил относительно той же оси
![]() Зако́н
сохране́ния моме́нта и́мпульса
– момент импульса замкнутой системы
сохраняется, т.е. не изменяется с течением
времени.
Зако́н
сохране́ния моме́нта и́мпульса
– момент импульса замкнутой системы
сохраняется, т.е. не изменяется с течением
времени.
№19Сравнение динамических характеристик поступательного и вращательного движения.

№20 Гармонические колебания и их характеристики. Виды колебаний
Виды колебаний:
свободные(собственные)-происходят
в системе выведенной изравновесия и
предоставленной самой себе,
вынужденные-колебательная
система подвергается периодическому
воздействию внешней силы, автоколебания(частота
внешних воздействий на систему задаётся
самой системой),параметрические(у
колеблющейся системы периодически
изменяется какой-либо параметр).Простейшим
видом колебаний являются гармонические
колебания(изменяющаяся
величина подчиняется закону синуса или
косинуса). ![]() x-координаты
груза(смещение груза).А-амплитуда
колебаний(амплитуда-это максимальное
смещение точки).
x-координаты
груза(смещение груза).А-амплитуда
колебаний(амплитуда-это максимальное
смещение точки).![]() –циклическая частота(круговая,собственная
частота системы).t-время.
–циклическая частота(круговая,собственная
частота системы).t-время.
![]() –начальная фаза.
–начальная фаза.![]() -фаза колебаний .Период-
минимальный промежуток времени, по
истечении которого колебания повторяются.
-фаза колебаний .Период-
минимальный промежуток времени, по
истечении которого колебания повторяются.
![]()
![]()
![]()
№21Дифференциальное уравнение гармонических колебаний. Квазиупругие силы.
1.используя формулу найдём сркоость колеблющейся по гармоническому закону точки.
![]()
2.найдём ускорение частицы, движущейся по гармоническому закону.
![]() =
=![]()
3.домножим обе
части формулы
на
массу колеблющихся частиц.![]()
По второму закону
Ньютона:![]() .Сравним
с законом
Гука(силы упругости):
.Сравним
с законом
Гука(силы упругости):![]() .Любую силу, стремящуюся вернуть систему
в положение равновесия называют
восстанавливающей, а из-за сходства с
силой упругости её называют квазиупругой.
.Любую силу, стремящуюся вернуть систему
в положение равновесия называют
восстанавливающей, а из-за сходства с
силой упругости её называют квазиупругой.
![]() k-коэффициент
упругости или жёсткость системы.Оказалось,
что частота гармонических колебаний
зависит только от свойств самой системы,
но не от амплитуды. Это свойство характерно
для малых колебаний.Из второго закона
Ньютона с учётом формул
k-коэффициент
упругости или жёсткость системы.Оказалось,
что частота гармонических колебаний
зависит только от свойств самой системы,
но не от амплитуды. Это свойство характерно
для малых колебаний.Из второго закона
Ньютона с учётом формул ![]()
![]() -дифференциальное
уравнение гармонических колебаний.
Его решение описывает колебательное
движение материальной точки, происходящее
под действием квазиупругой силы в
отсутствии сил сопротивления.
-дифференциальное
уравнение гармонических колебаний.
Его решение описывает колебательное
движение материальной точки, происходящее
под действием квазиупругой силы в
отсутствии сил сопротивления.
№22 Пружинный, физический, математический маятники (вывод периодов колебаний).Приведенная длина физического маятника.
Пружинный маятник — тело подвешенное на невесомой абсолютно упругой пружине и совершающее колебания под действием силы упругости. Физический маятник — абсолютно твердое тело, совершающее колебания под действием силы тяжести относительно горизонтальной оси, не проходящей через его центр тяжести. Математический маятник— материальная точка, подвешенная на невесомой, нерастяжимой нити и совершающая колебания под действием силы тяжести. Период пружинного маятника:w=(k/m)^0.5 тогда T=2пи(k/m)^0.5. Период физического маятника:
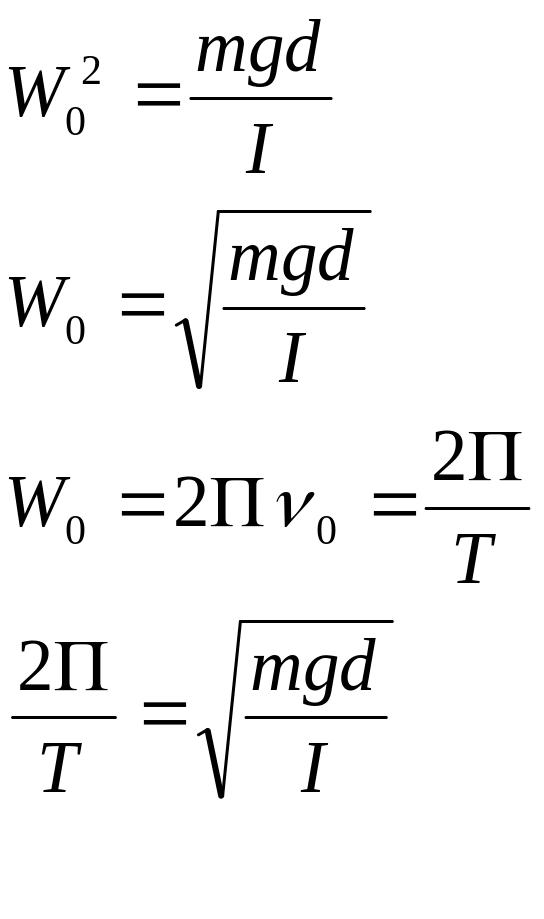 где I-момент
инерции ,l-длина
маятника,I=m*l^2,
для мат.маятника
где I-момент
инерции ,l-длина
маятника,I=m*l^2,
для мат.маятника
![]() =
=![]() Период
колебания математического маятника.
Период
колебания математического маятника.
Период математического маятника его малые колебания не зависят от угла, массы, но зависит от длины нити.
Приведенная длина
физического маятника
— длина такого математического маятника
период которого совпадал бы с данным
физическим маятником.
![]()
№23 Энергия гармонических колебаний
Потенциальная
энергия:![]()
Кинетическая
энергия:![]()
Полная энергия
:![]()
Максимально значение Wп иWктПри sin и cos равным 1
![]()
![]()
Wп=0 , Wk=Wk max
Wk=0 , Wп=Wпmax
Полная энергия остается постоянной, т.к. при гармонических колебаниях справедлив закон сохранения механической энергии, поскольку упругая сила консервативна.
№24 Дифференциальное уравнение затухающих колебаний и его решение. Апериодический процесс
Во всякой реальной
системе имеются силы сопротивления,
действия которых приводят к диссоциации
энергии. Если убыль энергии не восполнять
извне, то колебания будут затухать.При
малых скоростях силы сопротивления
пропорциональны скорости: ![]() r-коэффициент
пропорциональности.
r-коэффициент
пропорциональности.
Запишем второй закон Ньютона применительно к затухающим колебаниям:
![]() Fупр=-кх,
Fсопр.=-rx
Fупр=-кх,
Fсопр.=-rx
![]()
![]()
![]() -дифференциальное
уравнение затухающих колебаний.
-дифференциальное
уравнение затухающих колебаний.
Решения уравнения в случае слабых затуханий будет иметь вид:
![]() где
где ![]()
Слабое затухание
соответствует: ![]()
![]() -коэффициент затухания.
-коэффициент затухания.![]()
![]() -время затухания- время, за которое
амплитуда колебаний уменьшается в е
раз.
-время затухания- время, за которое
амплитуда колебаний уменьшается в е
раз.
Отношение амплитуд затухающего колебания, отличающихся на один период, называется декрементом затухания.
![]() Логарифмический
декремент затухания
Логарифмический
декремент затухания
![]()
Добротность:
![]()
Aпериодический процесс
При достаточно большом затухании (удельном сопротивлении = r/2m) о колебательный характер процесса возвращения к положению равновесия системы, выведенной из него, исчезает, превращаясь в монотонно убывающий процесс, называемый апериодическим. В этом случае трение, диссипация преобладают над упругостью. Такой режим реализуется, например, для движения рамки электроизмерительных приборов.
№25 Сложение гармонических колебаний с близкими частотами. Биения.
Колеблющиеся тело может участвовать в нескольких колебательных процессах, тогда чтобы найти результирующее колебание, иными словами, колебания нужно сложить
Рассмотрим случай когда частоты складываемых колебаний мало отличаются друг от друга.
Предположим, что амплитуды колебаний одинаковы, а начальные фазы равны 0
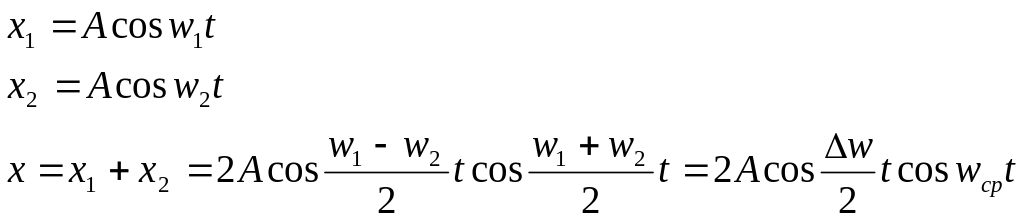 -уравнение
результирующего колебания
-уравнение
результирующего колебания
Периодическое изменение амплитуды результирующих колебаний при сложении гармонических колебаний с близкими частотами называется биением.
№26 Дифференциальное уравнение вынужденных колебаний и его решение.
Колебания, в которых диссипация энергии компенсируется с помощью периодической внешней силы, называются вынужденными, а сама сила- вынуждающая.
![]()
Из второго закона
Ньютона:![]() это:
это:![]() поделим на m
поделим на m
![]()
![]() - дифференциальное уравнение вынужденных
колебаний. Это уравнение можно свести
к ЛНДУ
- дифференциальное уравнение вынужденных
колебаний. Это уравнение можно свести
к ЛНДУ
![]() Его решение= сумме общего решения
Его решение= сумме общего решения
и частного решения
неоднородного уравнения:![]() Решение
диф.уравнения =сумме общего решения
однородного уравнения
Решение
диф.уравнения =сумме общего решения
однородного уравнения![]()
№27 Метод векторных диаграмм. Амплитуда вынужденных колебаний.
Векторной диаграммой называют графическое изображение гармонических колебаний в виде векторов на плоскости.
Из точки О вдоль
оси Х проведём вектор А и сместим этот
вектор относительно оси Х, вращая вокруг
точки О, на угол ![]()
![]()
Если этот вектор
привести во вращение относительно точки
О против часовой стрелки с частотой
,
то координата проекции А на ось Х будет
изменятся по гармоническому закону ![]() в пределах
в пределах ![]()
Амплитуда:
Найдём скорость:
из x=Asin(wt+фи)![]()
![]() подставим в
подставим в ![]() =поделим на А
=поделим на А
![]() По Пифагору
получим
По Пифагору
получим![]()
Отсюда амплитуда вынужденных колебаний будет равна:
![]()
№28 Механический резонанс
Явление резкого
возрастания амплитуды(до максимума)
вынужденных колебаний называется
резонансом.(обычные
качели.) Важно, что резонансная
частота не зависит от массы маятника.
Увеличение амплитуды - это лишь следствие
резонанса,
а причина
- совпадение внешней (возбуждающей)
частоты с внутренней (собственной)
частотой колебательной системы. Частота
вынужденных колебаний ![]() ,при
которой амплитуда вынужденных колебаний
достигает максимума, называется
резонансной.
Для определения
резонансной частоты вынуждающей силы,
следует исследовать функцию
на
экстремум.
,при
которой амплитуда вынужденных колебаний
достигает максимума, называется
резонансной.
Для определения
резонансной частоты вынуждающей силы,
следует исследовать функцию
на
экстремум.
![]() После дифференцирования формулы
После дифференцирования формулы![]() Это равенство выполняется при
Это равенство выполняется при![]() и
и ![]() ,
у которых только лишь положительное
значение имеет физический смысл.
Следовательно, резонансная частота
,
у которых только лишь положительное
значение имеет физический смысл.
Следовательно, резонансная частота
![]()
№29 Механизм образования волн в упругой среде. Поперечные и продольные волны.
Механизм: колебания, возбужденные в какой-либо точке среды распространяются в ней с конечной скоростью, зависящей от свойств среды, передаваясь от одной точки среды к другой. Чем дальше расположена частица среды от источника колебаний, тем позднее она начнет колебаться. При изучении распространения колебаний не учитывается молекулярное строение среды и среда рассматривается как сплошная(непрерывно распределена в пространстве, обладает упругими свойствами ). Основное свойство всех волн: перенос энергии без переноса вещества. Волнами называются колебательные процессы, передающиеся в пространстве от точки к точки. Среды, в которых возможна передача колебательных процессов называется упругими. Продольные волны — передача колебаний от точки к точке в них происходит в направлении распространения волн. Поперечные волны — колебание частиц среды происходит поперек направления распространения волн. В твердых телах возможны как продольные, так и поперечные волны. В жидких и газообразных только продольные. В газах( под поршнем газ уплотняется, а затем это уплотнение перемещается по оси цилиндра)
№30. Уравнение бегущей волны. Длина волны, волновое число, фазовая скорость.
Бегущими волнами
- волны, которые переносят в пространстве
энергию. Для вывода уравнения бегущей
волны- зависимости смещения колеблющейся
частицы от координат и времени- рассмотрим
плоскую волну,
предполагая что колебания носят
гармонический характер, а ось х
совпадает с
направлением распространения волны.
Уравнение
бегущей волны
:
![]() В
общем случае уравнение плоской волны
распространяющейся вдоль положительного
направления оси х в среде, не поглощающей
энергию, имеет вид:
В
общем случае уравнение плоской волны
распространяющейся вдоль положительного
направления оси х в среде, не поглощающей
энергию, имеет вид:![]() w-циклическая
частота, [в скобках]- фаза плоской волны.
w-циклическая
частота, [в скобках]- фаза плоской волны.
Длиной волны
- расстояние между ближайшими точками,
колеблющимися в одинаковой фазе.(
![]() )T—
время одного полного колебания всех
его точек.
)T—
время одного полного колебания всех
его точек.![]() где
где
![]() -частота волны.Важной характеристикой
волнового процесса является волновое
число К.
-частота волны.Важной характеристикой
волнового процесса является волновое
число К.![]() По
сколько из
По
сколько из
![]() то волновое число
то волновое число
![]()
v=dx/dt- фазовая скорость.(скорость перемещения фазы волны)
№31Принцип суперпозиции волн. Когерентность. Интерференция.
Принцип суперпозиции волн: при наложении 2 и > волн, результирующее смещение частиц среды в любой момент представляет собой геометрическую сумму смещений вызываемых каждой волной в отдельности. Существует особый частный случай суперпозиции волн— интерференция(явление, при котором существуют усиление или ослабление результирующей волны в зависимости от соотношения между фазами этих волн)Для возникновения интерференции, источники волн должны соответствовать условиям когерентности.
Одинаковые длины волн (одинаковые частоты)
Постоянна разность фаз.
Одинаковые скорости волн.
Направление колебаний частиц среды должны быть одинаковыми.
№32 Образование стоячих волн
Стоячие волны-волны,
образующиеся при наложении 2 бегущих
волн, распространяющихся навстречу
друг другу с одинаковыми частотами и
амплитудами, а в случае поперечных волн
еще и одинаковой поляризацией. Уравнение
стоячей волны:![]() .Образование
стоячих волн наблюдают при
интерференции бегущей и отраженной
волны. Если
конец веревки закрепить неподвижно(к
стене), то отраженная в месте закрепления
веревки волна будет интерферировать с
бегущей волной, образуя стоячую волну.
На границе, где происходит отражение
волны возникает узел(точка,
в которой амплитуда колебаний =0) Будет
ли на границе отражения узел или
пучность(точка,
в которой амплитуда колебаний максимальна)
зависит от соотношения
плотностей сред.
Если среда, от которой происходит
отражение, менее плотная, то в месте
отражения возникает пучность,
если более плотная-узел.
.Образование
стоячих волн наблюдают при
интерференции бегущей и отраженной
волны. Если
конец веревки закрепить неподвижно(к
стене), то отраженная в месте закрепления
веревки волна будет интерферировать с
бегущей волной, образуя стоячую волну.
На границе, где происходит отражение
волны возникает узел(точка,
в которой амплитуда колебаний =0) Будет
ли на границе отражения узел или
пучность(точка,
в которой амплитуда колебаний максимальна)
зависит от соотношения
плотностей сред.
Если среда, от которой происходит
отражение, менее плотная, то в месте
отражения возникает пучность,
если более плотная-узел.
№33 Обоснование МКТ. Статистический метод
МКТ изучает физ.свойства тел, в зависимости от их строения, сил взаимодействия между образующимися телами молекулами, характера теплового движения этих частиц.
Обоснование МКТ:
1.сжимаемость газов.
2.применение газами и жидкостями формы сосуда.
3.взаимное проникновение молекул разных веществ- диффузия.
4.испарение жидкости и (твёрдых тел-сублимация)
5.Броуновское движение.
6.растворение твердых тел(смешение газов и жидкостей)
Статистический метод исследования вещества- движение отдельной молекулы изучается по закону механики, а затем методом теории вероятностей определяют состояние системы, состоящей из большого числа частиц.
№34 Уравнение Менделеева-Клапейрона. Идеальный газ. Основное уравнение МКТ.
Уравнение состояния
идеального газа (уравнение Клапейрона
— Менделеева)
![]() ,где молярная газовая постоянная- R-8,31
Дж/(моль*К)
,где молярная газовая постоянная- R-8,31
Дж/(моль*К)
Идеальный газ- модель, принимаемая к любому газу при следующих условиях:
1.формой и размерами которой можно пренебречь- материальные точки.
2.столкновения между молекулами происходят абсолютно упруго.
3.взаимным притяжением молекул можно пренебречь - потенциальная энергия равна нулю.
Для выполнения этих условий необходимо чтобы:
1.газ был достаточно нагрет(молекулы должны двигаться достаточно быстро).
2.газ должен быть достаточно разрежен.
Если газ в объеме
V
содержит N
молекул, движущихся со скоростями v1,v2…
то целесообразно рассматривать среднюю
квадратичную скорость
![]() характеризующую
всю совокупность молекул газа.
характеризующую
всю совокупность молекул газа.
Основное уравнение
МКТ:![]()
№35 Распределение Максвелла
Закон Максвелла описывается некоторой функцией f(v)-функция распределения молекул по скоростям. Если разбить диапазон скоростей молекул на малые интервалы,(dv),то на каждый интервал скорости будет приходиться некоторое число молекул dN(v), имеющих скорость, заключенную в этом интервале. Функция f(v)- определяет относительное число молекул (dN(v))/N , скорости которых лежат в интервале от v до v+dv, т.е. (dN(v))/N= f(v)dv
Откуда f(v)=dN(v)/Ndv
Применяя методы теории вероятностей,
Максвелл нашел функцию f(v)-закон
распределения молекул идеального газа
по скоростям:
![]() Перед
законом:Постоянная
Перед
законом:Постоянная
![]() тогда
тогда
![]()
Распределение Максвелла зависит от рода газа и от состояния системы,
Распределение Максвелла как и функция начинается, в 0 достигает максимума, а затем асимптотически стремится к 0.
![]()
№36 Вывод формулы наиболее вероятной скорости
Скорость, при которой функция распределения молекул идеального газа по скоростям максимальна-наиболее вероятная скорость. Исследуем функцию на экстремум: возьмем производную по v и прировняем к 0.
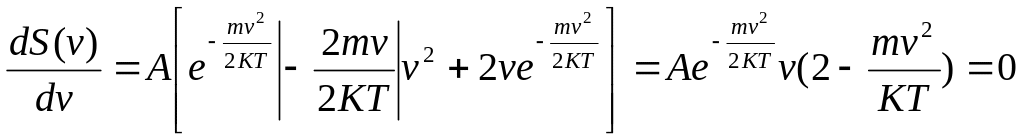
Это уравнение имеет 3 корня, 2 из которых соответствуют минимуму функции.
V=0
V=![]()
![]()
![]()
При увеличении t или уменьшении массы молекулы газа V-вероятно возрастает, т.е. максимум функции смещается в право и высота этого графика уменьшается.
№37 Барометрическая формула
Барометрическая формула устанавливает зависимость между давлением атмосферного воздуха и высотой его над уровнем моря.
Зависимость p от (h) требует сформулировать модель атмосферного воздуха.
Сделаем ряд упрощений:
Ускорение свободного падения g=const
Считаем воздух идеальным газом.
Полагаем воздух однородным газом
Систему считать изотермической.T=const
Выберем столб атмосферного воздуха. Найдем разности давлений
![]() следует
следует
![]()
Из уравнения
![]() видно
что
видно
что
![]()
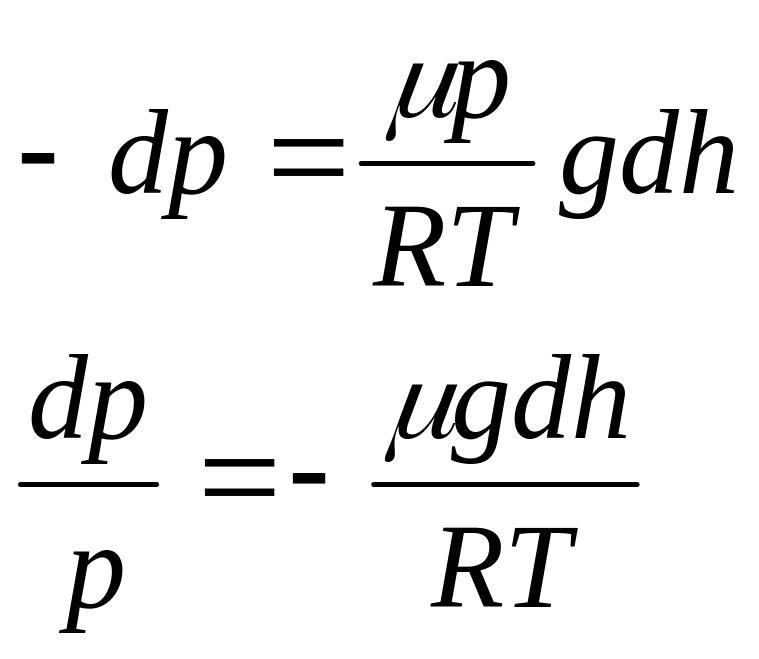 или
или
Интегрируем полученное выражение
![]() тогда
тогда
![]()
Найдем С из
уравнения что h=0
![]() =
=![]()
![]()
![]()
Из следует, что давление убывает с высотой тем быстрее чем:
Тяжелее газ
Чем ниже температура (t)
38 Распределение Больцмана
Поскольку
![]() подставим
это выражение в формулу
подставим
это выражение в формулу
![]()
В показатели
степени![]()
![]() -Распределение
Больцмана, где
Wn-
потенциальная энергия
-Распределение
Больцмана, где
Wn-
потенциальная энергия
Из него следует, что при данной температуре плотность газа больше там, где меньше потенциальная энергия его молекул. Его частицы имеют одинаковую массу и находятся в состоянии хаотического теплового движения, то распределение Больцмана справедливо в любом внешнем потенциальном поле, а не только в поле сил тяжести.
№39 Эффективный диаметр молекул. Длина свободного пробега. Сила и потенциальная энергия межмолекулярного воздействия. Релаксация. Равновесные и неравновесные состояния
Длина свободного пробега-некоторый путь L, который проходят молекулы между 2 последовательными столкновениями. Траектория движения одной молекулы представляет собой ломаную линию. Значит, расстояние между последовательными столкновениями оказывается неодинаковыми, поэтому можно говорить о средней длине свободного пробега <L>
![]()
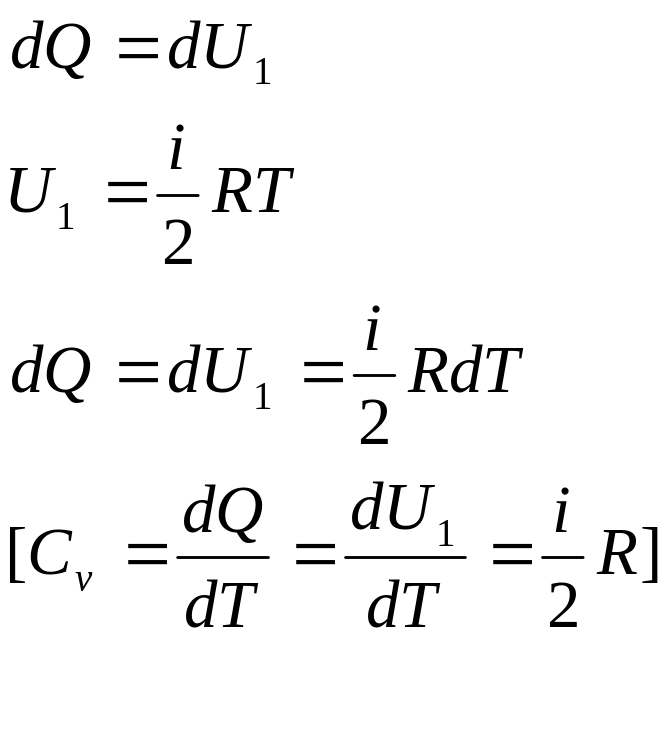
![]() Эффективный
диаметр -
минимальное расстояние между центрами
взаимодействующих молекул. Он зависит
от скорости сталкивающихся молекул,
т.е. от температуры газов(несколько
уменьшается с ростом температуры)Не
всегда параметры системы имеют
определённые значения, тогда состояние
системы называется неравновесным.
Если систему изолировать, то через
определённое время система перейдёт в
равновесное
состояние. Переход
системы из одного состояния в другое
называется процессом. Переход в
равновесное состояние называется
релаксацией
системы.
Временем
релаксации
называется длительность перехода
системы в равновесное состояние.
Эффективный
диаметр -
минимальное расстояние между центрами
взаимодействующих молекул. Он зависит
от скорости сталкивающихся молекул,
т.е. от температуры газов(несколько
уменьшается с ростом температуры)Не
всегда параметры системы имеют
определённые значения, тогда состояние
системы называется неравновесным.
Если систему изолировать, то через
определённое время система перейдёт в
равновесное
состояние. Переход
системы из одного состояния в другое
называется процессом. Переход в
равновесное состояние называется
релаксацией
системы.
Временем
релаксации
называется длительность перехода
системы в равновесное состояние.
№40 Явления переноса: опытные законы диффузии, теплопроводности и внутреннего трения (вязкости).
В термодинамических неравновесных системах возникают особые необратимые процессы-явления переноса, в результате которых происходит пространственный перенос энергии, массы, импульса. Диффузия(закон Фика) - перенос массы под действием градиента концентрации (плотности).Теплопроводность(Фурье) - перенос теплоты (внутренней энергии) под действием градиента температуры. Вязкость(Ньютон) (внутреннее трение) - перенос импульса под действием градиента скорости направленного движения
При малых отклонениях от состояния равновесия возникающие потоки переносимых величин прямо пропорциональны соответствующим градиентам и описываются феноменологическими уравнениями следующего вида:
![]() =
- Кgrad
X , где:
=
- Кgrad
X , где:
 -
плотность
потока переносимой величины (теплоты
- в теплопроводности, импульса
в
вязкости, массы в диффузии), т. е. вектор,
численно равный количеству величины,
переносимой за единицу времени через
единичную площадку, нормальную к
направлению переноса;Х - величина
(температура - в теплопроводности,
скорость - в вязкости, плотности - в
диффузии), пространственная неоднородность
которой и обусловливает неравновесность
состояния макросистемы; К - коэффициент
пропорциональности, мера интенсивности
того или иного явления переноса. Знак
” -” указывает,
что импульс, теплопроводность, массы
переносится в направлении убывания
скорости, температуры, плотности
соответственно.
-
плотность
потока переносимой величины (теплоты
- в теплопроводности, импульса
в
вязкости, массы в диффузии), т. е. вектор,
численно равный количеству величины,
переносимой за единицу времени через
единичную площадку, нормальную к
направлению переноса;Х - величина
(температура - в теплопроводности,
скорость - в вязкости, плотности - в
диффузии), пространственная неоднородность
которой и обусловливает неравновесность
состояния макросистемы; К - коэффициент
пропорциональности, мера интенсивности
того или иного явления переноса. Знак
” -” указывает,
что импульс, теплопроводность, массы
переносится в направлении убывания
скорости, температуры, плотности
соответственно.
№41 Степени свободы. Закон равнораспределения энергии.
Молекула идеального газа- это материальная точка, которая не имеет размеров, такая частица может двигаться только поступательно.У частиц более сложной формы приходится учитывать и вращательное движение. Молекула может быть абсолютно упругим телом, в ней могут происходить изменения взаимного расположения атомов- колебания.
Числом степеней свободы механической системы называется количество независимых величин, определяющих положение системы в пространстве.
Вид молекулы |
поступательная |
вращательная |
колебательная |
Вид связи |
Одноатомная молекула(идеальный газ) |
3 |
--- |
--- |
--- |
Двух атомная молекула |
3 |
2 |
--- |
жёсткая |
двухатомная |
3 |
2 |
1 |
упругая |
Трёхатомная(абсолютно твёрдое тело) |
3 |
3 |
--- |
жёсткая |
Трёх и более атомная |
3 |
3 |
3N-6 |
упругая |
Средняя энергия,
приходящаяся на одну степень свободы
(поступательную, вращательную,
колебательную) одинакова и равна
![]() ,тогда
средняя энергия молекулы, имеющая i
степеней свободы равна :
,тогда
средняя энергия молекулы, имеющая i
степеней свободы равна :
![]() -закон
равнораспределения энергии(для
статистической системы, находящейся в
состоянии термодинамического равновесия,
на каждую поступательную и вращательную
степени свободы приходится в среднем
кин.энергия=
,
а на каждую колебательную степень
свободы- в среднем энергия, равная кТ)
-закон
равнораспределения энергии(для
статистической системы, находящейся в
состоянии термодинамического равновесия,
на каждую поступательную и вращательную
степени свободы приходится в среднем
кин.энергия=
,
а на каждую колебательную степень
свободы- в среднем энергия, равная кТ)
№42 Внутренняя энергия идеального газа. 1-ое начало термодинамики. Работа при изменении объема газа
Внутренняя энергия-энергия хаотического(теплового)движения микрочастиц системы(молекул,атомов,ядер)и энергия взаимодействия этих частиц.Значит, что к внутренней энергии не относятся кин.энергия движения системы как целого и пот. энергия системы во внешних полях, входит кинетическая энергия хаотического движения молекул и потенциальная энергия взаимодействия атомов в молекулах и молекул между собой.
![]() - Внутренняя
энергия на один моль идеального газа
- Внутренняя
энергия на один моль идеального газа
![]() -
Внутренняя
энергия газа. Работа-
-
Внутренняя
энергия газа. Работа-![]()
![]() -давление
-давление ![]() Первое начало
термодинамики-
это частный случай закона сохранения
энергии.
Первое начало
термодинамики-
это частный случай закона сохранения
энергии.![]()
![]() +dA-работа
над внешними силами.-dA-работа
внешних тел над системой. Формулировка
1-ое начало
термодинамики:
+dA-работа
над внешними силами.-dA-работа
внешних тел над системой. Формулировка
1-ое начало
термодинамики:
1) Количество теплоты, полученное системой, идёт на изменение её внутренней энергии и совершение работы против внешних сил.
2) Изменение внутренней энергии системы при переходе её из одного состояния в другое равно сумме работы внешних сил и количества теплоты, переданного системе и не зависит от способа, которым осуществляется этот переход
3)вечный двигатель 1-ого рода- периодически действующий двигатель, который совершал бы большую работу, чем сообщенная ему извне энергия, не возможен.(A=Q,т.е. система иногда возвращается в первоначальное состояние)
№43 Виды теплоемкостей. Теплоемкость при постоянном объеме
Теплоемкость
тела —
величина определяющая количество
теплоты, необходимой для нагревания
тела на 1К.![]()
![]()
Удельная
теплоемкость-теплоемкость
единичной массы тела![]()
Молярная
теплоемкость-величина,
= количеству теплоты, необходимому для
нагревания 1 моля вещества на 1 К.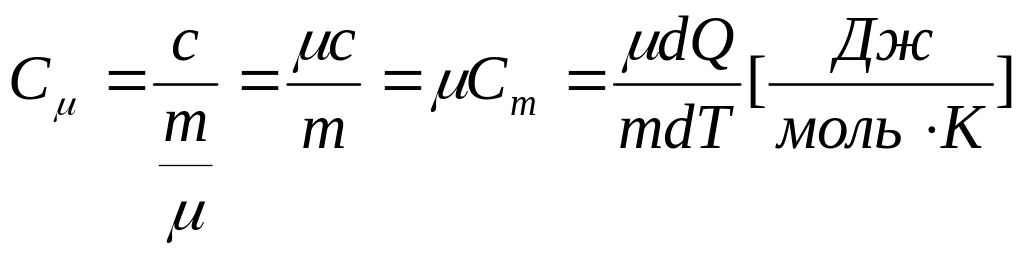 Теплостойкость
при постоянном объеме.V=constРассмотрим
молярную теплоемкость идеального газа
Теплостойкость
при постоянном объеме.V=constРассмотрим
молярную теплоемкость идеального газа
![]() Изменение v=0,
значит
Изменение v=0,
значит
№44 Теплоемкость при постоянном давлении. Уравнение Майера. Показатель адиабаты.
Изобарный процесс— термодинамический процесс, происходящий в системе при постоянном внешнем давлении; на термодинамической диаграмме изображается изобарой.
P=const.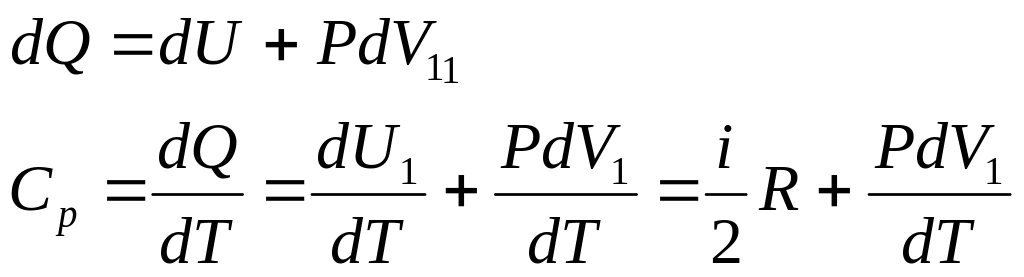
Зависимость V от T найдем из уравнения Менделеева-Клапейрона
![]()
![]()
![]() -
Теплоемкость при постоянном давлении
-
Теплоемкость при постоянном давлении
Из
![]() с учетом
с учетом
![]() .
.
![]() - уравнение
Майера.
Физический смысл уравнения- работа,
совершаемая одним молем идеального
газа, при его нагревании на 1К. При P=const
численно равна универсальной газовой
постоянной.
Адиабатный процесс-процесс,
при котором отсутствует теплообмен
между системой и окружающей среды.
- уравнение
Майера.
Физический смысл уравнения- работа,
совершаемая одним молем идеального
газа, при его нагревании на 1К. При P=const
численно равна универсальной газовой
постоянной.
Адиабатный процесс-процесс,
при котором отсутствует теплообмен
между системой и окружающей среды.![]() =
Сп/Св
- показатель адиабаты(коэффициент
Пуассона)
=
Сп/Св
- показатель адиабаты(коэффициент
Пуассона)
№45Статистическое толкование энтропии. Второе начало термодинамики и его смысл. Гипотеза о тепловой смерти Вселенной
Функция состояния, дифференциалом которой является δQ/T=dS-Энтропия(S).Энтропия замкнутой системы может либо возрастать(необратимый процесс), либо оставаться постоянной(обратимый процесс).Энтропия определяется с точностью до аддитивной постоянной. Значение постоянной не играет роли, т.к. физический смысл имеет не сама энтропия, а разность энтропий. Энтропия имеет свойство аддитивности: энтропия системы= сумме энтропий тел, входящих в систему. Второе начало термодинамики: в процессах, происходящих в замкнутой системе, энтропия не убывает. По Больцману: возрастание энтропии означает переход системы из менее вероятных в более вероятные состояния. По Кельвину: невозможен круговой процесс, единственный результат- превращение теплоты, полученной от нагревателя, в работу. По Клаузиусу: невозможен круговой процесс, единственный результат-передача теплоты от менее нагретого тела к более нагретому. Гипотеза о тепловой смерти Вселенной: Рассматривая Вселенную как замкнутую систему и применяя к ней Второе начало термодинамики, Клаузиус свел его содержание к утверждению, что энтропия Вселенной должна достигнуть своего максимума. Это означает, что со временем все формы движения должны перейти в тепловую. Переход же теплоты от горячих тел к холодным приведет к тому, что температура всех тел сравняется, т.е. наступит полное тепловое равновесие и все процессы во Вселенной прекратятся- наступит тепловая смерть. Ошибочность вывода о тепловой смерти Вселенной заключается в том, бессмысленно применять 2 начало термодинамики к незамкнутым системам(Вселенная)
№46 Уравнение адиабаты(вывод)
Адиабатическим
называется процесс, протекающий без
теплообмена с окружающей средой Q=const
Согласно первому началу термодинамики
для идеального газа.![]() поскольку
поскольку
![]() т.е.
Внешняя работа совершается за счет
изменения внутренней энергии системы.
Перепишем уравнение
т.е.
Внешняя работа совершается за счет
изменения внутренней энергии системы.
Перепишем уравнение
![]() в виде:
в виде:
![]() Продиффер.
Уравнение состояния для идеального
газа, получим
Продиффер.
Уравнение состояния для идеального
газа, получим
![]() Исключим из последних температуру
Т:
Исключим из последних температуру
Т:![]() Разделив
переменные и учитывая, что
Разделив
переменные и учитывая, что![]() найдем
найдем
![]() Интегрируя
это ур-ние в пределах от р1 и р2, V1
и V2,
а затем потенцируя, придем к
Интегрируя
это ур-ние в пределах от р1 и р2, V1
и V2,
а затем потенцируя, придем к
![]() .Т.к.
состояния 1 и 2 выбраны произвольно, то
можно записать:
.Т.к.
состояния 1 и 2 выбраны произвольно, то
можно записать:![]() -уравнение
аддиабаты.(Пуассона)
-уравнение
аддиабаты.(Пуассона)
№47 обратимые и необратимые процессы. КПД тепловой машины. Цикл Карно
Обратимый процесс
может быть проведен в обратном порядке
через те же состояния, что и при прямом
ходе. Необратимые
процессы
сопровождаются изменениями окружающей
среды. КПД=![]() В.
Томсон: Невозможно осуществление цикла
теплового двигателя без переноса
некоторого количества теплоты от
источника тепла с более высокой
температурой к источнику с более низкой
температурой. Для превращения тепла в
работу необходим, кроме источника тепла,
охладитель, т.е. температурный перепад.
В периодическом процессе (цикле) только
часть теплоты, за счет которой
осуществляется цикл, может быть превращена
в работу. В любом цикле нельзя перевести
все подведенное тепло в работу.
В.
Томсон: Невозможно осуществление цикла
теплового двигателя без переноса
некоторого количества теплоты от
источника тепла с более высокой
температурой к источнику с более низкой
температурой. Для превращения тепла в
работу необходим, кроме источника тепла,
охладитель, т.е. температурный перепад.
В периодическом процессе (цикле) только
часть теплоты, за счет которой
осуществляется цикл, может быть превращена
в работу. В любом цикле нельзя перевести
все подведенное тепло в работу.
Карно нашел КПД идеальной тепловой машины, она должна при работе использовать только изотермические и адиабатические процессы.
![]()
![]()
Цикл Карно́ — идеальный цикл тепловой машины.. Тепловая машина Карно, работающая по этому циклу, обладает максимальным КПД из всех машин, у которых максимальная и минимальная температуры осуществляемого цикла совпадает соответственно с максимальной и минимальной температурами цикла Карно.
Одним из важных свойств цикла Карно является его обратимость: он может быть проведён как в прямом, так и в обратном направлении, при этом энтропия аддиабатически изолированной (без теплообмена с окружающей средой) системы не меняется.
.
№50 Уравнение Ван-дер-Ваальса. Модель реального газа Ван-дер-Ваальса
Наличие сил отталкивания, которые противодействуют проникновению в занятый молекулой объем других молекул, что фактический свободный объем, в котором могут двигаться молекулы реального газа, будет не V_m,а V_m-b, где b- объем занимаемый самими молекулами. Объем b =учетверенному собственному объему молекул. Действие сил притяжения газа приводит к появлению внутреннего давления. (p=a/V_m^2) a –постоянная Ван-дер-Ваальса, V_m-молярный объем. Вводя эти поправки, Уравнение Ван-дер-Ваальса для 1 моля газа(p+a/V_m^2)*(V_m-b)=RT. Для произвольного количества вещества (n=m/M) Уравнение Ван-дер-Ваальса(p+(n^2*a)/(V^2))*(V/n-b)=RT
