1 Вариант. 2 вариант.

3 вариант. 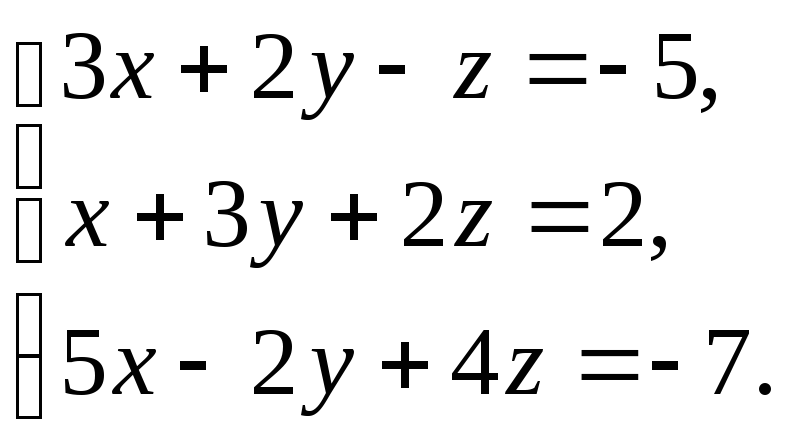4 вариант.

5 вариант. 6 вариант.

7 вариант. 8 вариант.

9 вариант. 10 вариант.

11 вариант.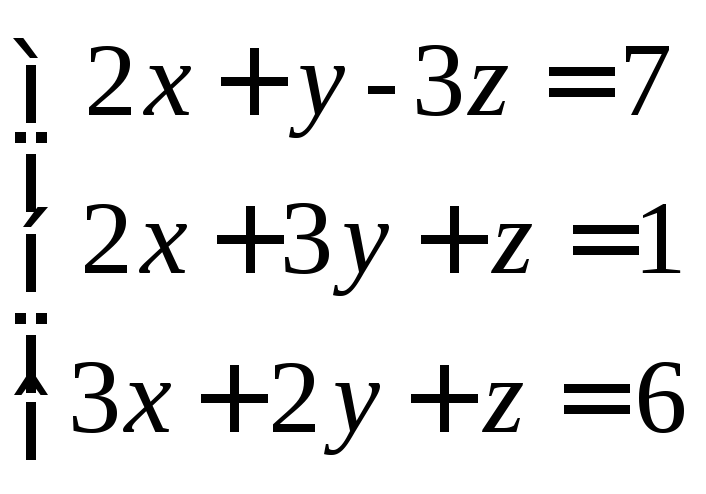 12 вариант.

13 вариант. 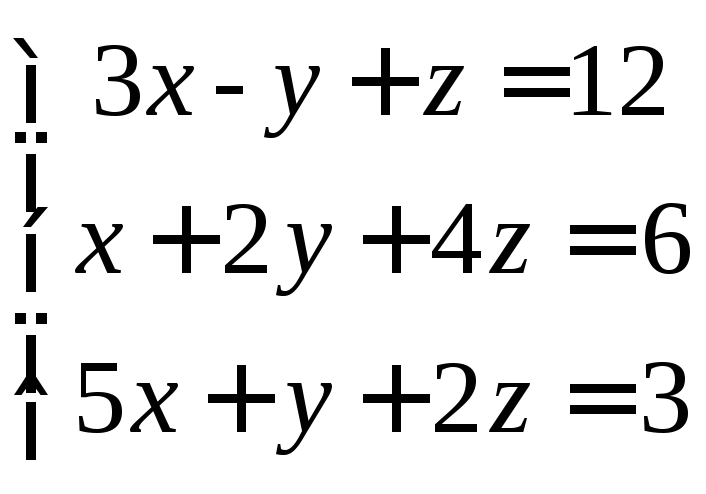14 вариант.

15 вариант. 16 вариант.

17 вариант. 18 вариант.

19 вариант. 20 вариант.

Образец решения типового варианта

Задача 1. Написать разложение вектора по векторам

Решение.

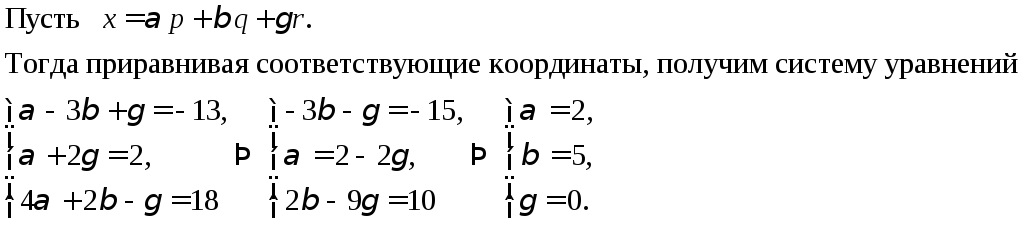
Задача 2.Коллинеарны ли векторыи, построенные по векторами?

Решение.

Вычисляем координаты векторов

Они пропорциональны

векторы иколлинеарны.

Задача 3.Найти косинус угла между векторамии.

Решение.

Задача 4. Вычислить площадь параллелограмма, построенного на векторах и.

Решение.

S=31 кв.ед.

Задача 5. Компланарны ли векторы ,и.

Решение.

Составляем определитель из координат векторов. Если он равен нулю, векторы компланарны.

векторы ,ине компланарны.

Задача 6. Вычислить объем тетраэдра с вершинами в точкахи его высоту, опущенную из вершинына грань.

Решение.

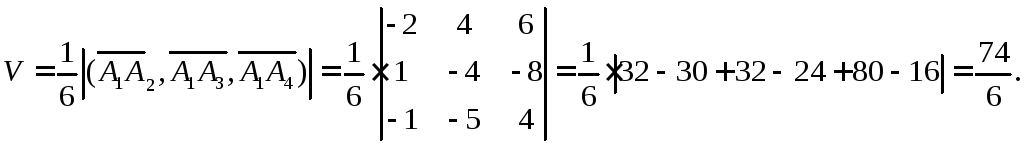
Задача 7. Найти расстояние от точкидо плоскости, проходящей через точки.

Решение.

Уравнение плоскости, проходящей через 3 точки

d=11.

Задача 8.Написать уравнение плоскости, проходящей через точкуперпендикулярно вектору.

Решение.

Находим

Т.к. вектор искомой плоскости, то его можно взять в качестве вектора нормали, следовательно

Ответ: 3x-y-z+6=0 .

Задача 9.Найти угол между плоскостями

Решение.

Находим векторы, угол между которыми соответствует искомому углу между плоскостями.

То есть плоскости параллельны.

Задача 12.Написать канонические уравнения прямой.

Решение.

Направляющий вектор прямой найдем так

Найдем координаты одной из точек, через которые проходит искомая прямая. Для этого дадим координатепроизвольное значение, например,, которое подставим в уравнения заданных плоскостей.

Итак, получается точка с координатами

Тогда уравнение прямой имеет вид

Задача 13.Найти точку пересечения прямой и плоскости.

Подставим в уравнение плоскости

Полученное значение подставим в систему

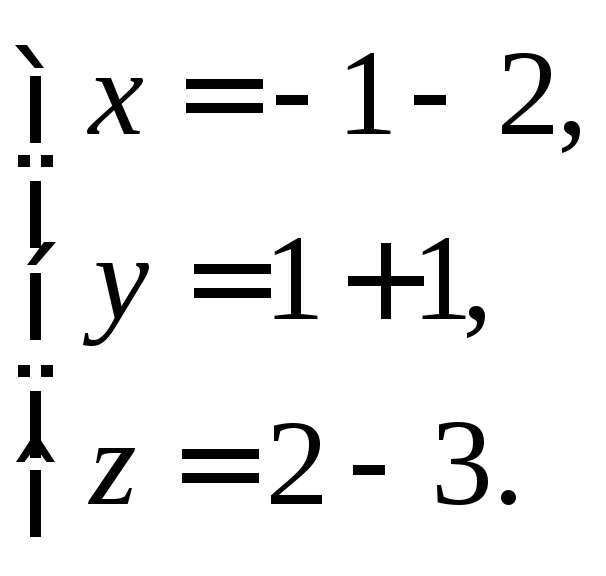
Таким образом, координаты искомой точки

Задача 14.Вычислить сумму матрицkA+mB,

если , k=2, m=-3

Решение:

Элементы матрицы суммы определяются по формуле:

С_ij=ka_ij+mb_ij.

Вычислим элементы первой строки матрицы суммы:

С₁₁=2·1+(-3) ·(-1)=5; С₁₂=2·2+(-3) ·6=-14; С₁₃=2·3+(-3) ·(-3)=15.

Аналогично вычисляем остальные элементы:

С₂₁=2·4+(-3) ·0=8; С₂₂=2·5+(-3) ·2=4; С₂₃=2·6+(-3) ·(-5)=27.

С₃₁=2·7+(-3) ·1=11; С₃₂=2·8+(-3) ·10=-14; С₃₃=2·9+(-3) ·7=-9.

Таким образом, матрица суммы примет вид:

Задача 15,a. Дана система из трех уравнений с тремя неизвестными. Установить, что система уравнений имеет единственное решение и найти его с помощью обратной матрицы

.

Решение.

Если определитель системы отличен от нуля, то система имеет единственное решение (теорема Крамера).

Вычислим определитель данной системы :

,

следовательно, система имеет единственное решение.

Данную систему можно записать в матричной форме :

, где ,,.

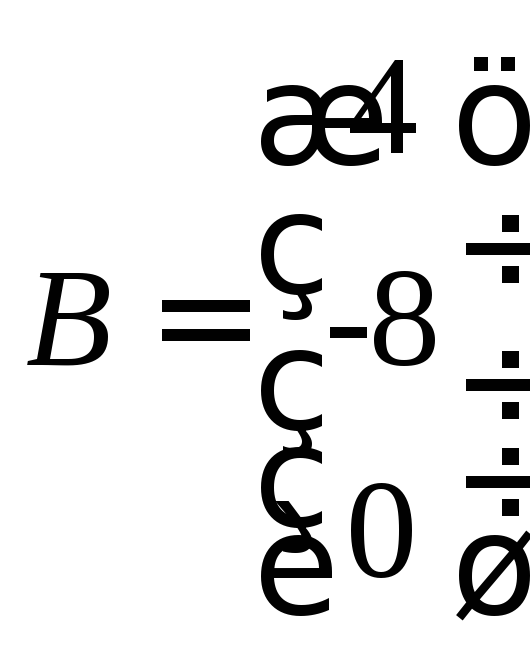Так как , то для матрицысуществует обратная матрица. Умножив матричное уравнениеслева на, получим, откуда, или.

Найдем обратную матрицу по формуле

,

где алгебраическое дополнение элемента.

,

,

.

.

Тогда

.

Ответ:.

Задача 15,б.

Методом Крамера найти решение системы линейных алгебраических уравнений

.

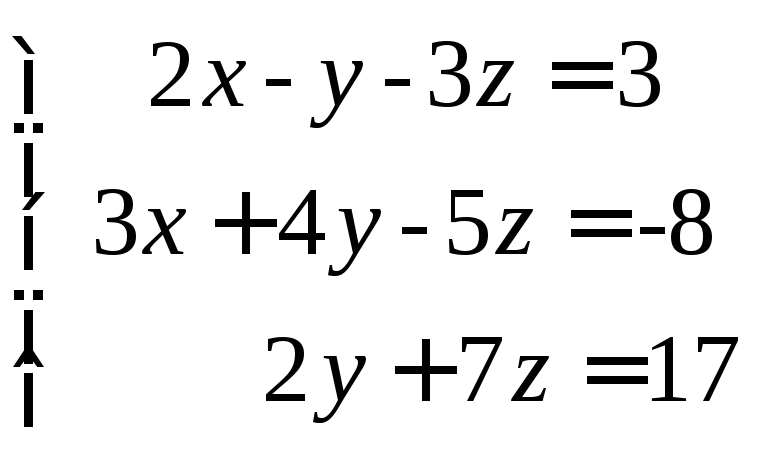Решение.