Для заметок

Тема 4. «Ряды динамики»

Задача 11. Реализация продукции магазином (тыс. руб.) в 2006 – 2008 годах характеризовалось следующими данными (на конец месяца):

Месяц	Реализация продукции (на конец месяца, тыс. руб.)
	2006	2007	2008
Январь	401,3	412,5	374,6
Февраль	286,6	335,1	245,5
Март	332,5	348,5	304,6
Апрель	197,8	198,4	171,1
Май	209,7	220,8	210,8
Июнь	294,4	323,0	321,3
Июль	275,0	281,4	244,7
Август	329,7	399,0	345,6
Сентябрь	476,5	531,8	495,4
Октябрь	503,6	551,0	523,2
Ноябрь	408,7	428,1	385,3
Декабрь	341,8	283,0	274,2

По данным 2008 года необходимо:

а) определить тип ряда динамики;

б) произвести анализ уровней ряда динамики цепным и базисным способами (за базисный принять уровень января 2008 года);

в) найти средние значения уровней ряда динамики и его числовых характеристик.

1. Рядом динамики называется способ записи случайной величины (признака, фактора) Y, при котором ее значения (уровни) приведены в зависимости от времени. Если- интервал времени (например, месяц, квартал, год и т. д.), то ряд динамики есть интервальный. Если же значения уровней приведены на определенную дату (например, начало месяца, конец квартала, начало года и т. д.), то ряд динамики есть моментный. Различают также ряды динамики с равноотстоящими и неравноотстоящими по времени уровнями. Ряд динамики принято представлять в виде таблицы:

			…
			…

2. Сравнение уровней ряда динамики производится двумя способами: цепным и базисным. При первом способе данный уровень сравнивается с предыдущем ему уровнем. Во втором случае выбирается базисный уровень(не обязательно первый) и все остальные уровни сравниваются с ним. Имеют место следующие

основные показатели, характеризующие изменения уровней ряда динамики: абсолютный прирост, коэффициент роста, темп роста, темп прироста, абсолютное значение одного процента прироста (расчет этого показателя имеет экономический смысл только на цепной основе). Их расчетные формулы приведены в таблице:

Показатель	Обозначение	Расчетная формула
		Цепной способ сравнения	Базисный способ сравнения
Абсолютный прирост
Коэффициент роста
Темп роста
Темп прироста
Абсолютное значение одного процента прироста	|%|	или	-

3. В зависимости от типа ряда динамики среднее значение его уровней подсчитывается по формуле:

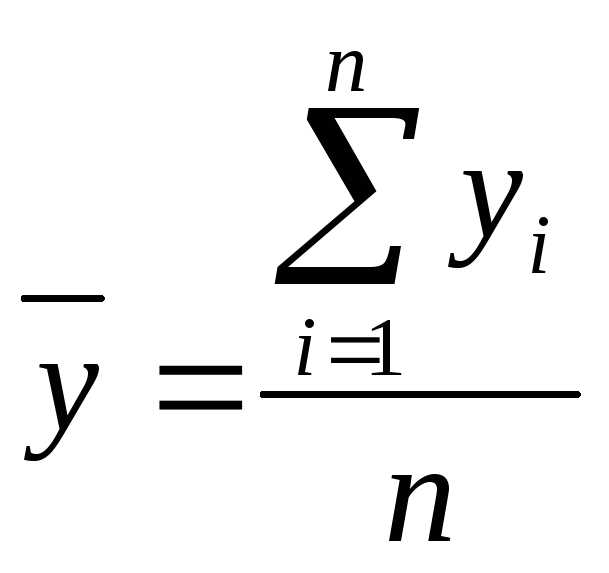
- если ряд динамики интервальный с равностоящими уровнями;

- если ряд динамики интервальный с неравноотстоящими уровнями,

- временная разность между данным и следующим уровнем, ;

- если ряд динамики моментный с равноотстоящими уровнями;

- если ряд динамики моментный с неравноотстоящими уровнями,

- временная разность между данным и следующим уровнем.

Среднее значение абсолютного прироста равно:

.

Величина среднего значения коэффициента роста равна:

.

Среднее значение темпов роста подсчитывается по формуле:

.

Наконец, среднее значение темпов прироста рассчитывается следующим образом:

.

Переходим к решению задачи. Так как значения уровней приведены на определенную дату (конец месяца), временная разность между уровнями постоянная (1 месяц), то рассматриваемый ряд динамики является моментным с равноотстоящими уровнями.

Найдем числовые характеристики уровня ряда динамики. Результаты расчетов помещены в таблицу 13.

В качестве примера произведем анализ строки таблицы 13, соответствующей октябрю месяцу. В октябре 2008 года магазин реализовал продукции на 523,2 тыс. руб., что на 27,8 тыс. руб. больше по сравнению с сентябрем и на 148,6 тыс. руб. больше по сравнению с январем 2008 года. Следовательно, реализация продукции в октябре увеличилась в 1,0561 раза по сравнению с октябрем и в 1,3967 раза по сравнению с январем. Уровень реализации в октябре составил 105,6116% от сентябрьского и 139,669% от январского уровня реализации. Таким образом, продукции в октябре реализовано на 5,6116% больше по сравнению с сентябрем и на 39,669% больше по сравнению с январем месяцем. Величина абсолютной величины одного процента прироста составила 4,954 тыс. руб.

Таблица 13

		, тыс. руб.				, %		, %		|%|, тыс. руб.
		С пред. месяцем	С январем 2008 г.	С пред. месяцем	С январем 2008 г.	С пред. месяцем	С январем 2008 г.	С пред. месяцем	С январем 2008 г.
1	374,6	-	0	-	1	-	100	-	0	-
2	245,5	-129,1	-129,1	0,6554	0,6554	65,5366	65,5366	-34,4634	-34,4634	3,746
3	304,6	59,1	-70	1,2407	0,8131	124,0733	81,3134	24,0733	-18,6866	2,455
4	171,1	-133,5	-203,5	0,5617	0,4568	56,1720	45,6754	-43,8280	-54,3246	3,046
5	210,8	39,7	-163,8	1,2320	0,5627	123,2028	56,2734	23,2028	-43,7266	1,711
6	321,3	110,5	-53,3	1,5242	0,8577	152,4194	85,7715	52,4194	-14,2285	2,108
7	244,7	-76,6	-129,9	0,7616	0,6532	76,1594	65,3230	-23,8406	-34,6770	3,213
8	345,6	100,9	-29	1,4123	0,9226	141,2342	92,2584	41,2342	-7,7416	2,447
9	495,4	149,8	120,8	1,4334	1,3225	143,3449	132,2477	43,3449	32,2477	3,456
10	523,2	27,8	148,6	1,0561	1,3967	105,6116	139,6690	5,6116	39,6690	4,954
11	385,3	-137,9	10,7	0,7364	1,0286	73,6430	102,8564	-26,3570	2,8564	5,232
12	274,2	-111,1	-100,4	0,7117	0,7320	71,1653	73,1981	-28,8347	-26,8019	3,853

Найдем среднее значение уровней ряда динамики. Имеем: среднемесячный объем реализации продукции магазином составил в 2008 году

324,7 (тыс. руб.).

Так как

,

то заключаем, что ежемесячное падение объемов реализации продукции в 2008 году составляло в среднем 9,1 тыс. руб.

Среднее значение коэффициента роста равно

.

Это означает, что месячный уровень объема реализации составляет в среднем 0,972 от предыдущего месяца или (согласно формуле среднего значения темпов роста)

.

Итак, в среднем в месяц, объем продаж сокращался на 2,8% по сравнению с предыдущим месяцем, так как

.

Задача 12. По данным задачи 11 (рассмотреть данные 2008 года) построить уравнение линейной функции тренда.

На формирование значение уровней ряда динамики основное влияние оказывают долговременные факторы, формирующие общую, в длительной перспективе тенденцию развития признака. Результат действия этих факторов моделируется в виде функции тренда

.

В частности, если тренд – линейный, то

.

Параметры a и b могут быть найдены методом наименьших квадратов путем решения системы нормальных уравнений:

.

Решая ее, получаем:

.

Все необходимые расчеты делаем в таблице:

1	1	1	374,6	374,6
2	2	4	245,5	491
3	3	9	304,6	913,8
4	4	16	171,1	684,4
5	5	25	210,8	1054
6	6	36	321,3	1927,8
7	7	49	244,7	1712,9
8	8	64	345,6	2764,8
9	9	81	495,4	4458,6
10	10	100	523,2	5232
11	11	121	385,3	4238,3
12	12	144	274,2	3290,4
	78	650	3896,3	27142,6

Получаем:

, .

Итак, уравнение функции тренда имеет вид:

.

Задача 13. Построить индексы сезонности за 2008 год и за 2006 – 2008 г.г. Результаты представить графически.

Помимо долговременных, на формирование значений уровней ряда динамики оказывают влияния сезонные факторы, определяющие периодическое изменение значений признака в определенные моменты времени (сезоны), причем эти изменения для каждого сезона можно считать постоянной величиной.

Самым простым способом учета сезонных факторов является расчет индексов сезонности, которые для одного года равны:

,

при этом - значение уровня ряда динамики в момент времени в данный момент времени (сезон), а- среднее значение уровней ряда динамики.

С целью избежания влияния случайных факторов, на практике, расчет индексов сезонности производится не за один, а за лет. В этом случае

,

где

- среднее значение уровней ряда динамики,

соответствующих определенному сезону,

- среднее значение уровней ряда динамики за лет.

После того как значения индексов сезонности рассчитаны, результаты удобно представить графически в виде ломаной с вершинами в точках с координатами (;). Также на координатной плоскости удобно изобразить линию . С ее помощью можно увидеть, в каких случаях мы имеем значения ряда динамики ниже среднего уровня, а в каких – выше.

Рассчитываем значения индексов сезонности в таблице (обратить внимание на расчет средних значений, ряд – моментный!):

	2006 г.	2007 г.	2008 г.
1	401,3	412,5	374,6	1188,4	396,1333	1,1536	1,1648
2	286,6	335,1	245,5	867,2	289,0667	0,7560	0,8500
3	332,5	348,5	304,6	985,6	328,5333	0,9380	0,9660
4	197,8	198,4	171,1	567,3	189,1000	0,5269	0,5560
5	209,7	220,8	210,8	641,3	213,7667	0,6492	0,6286
6	294,4	323	321,3	938,7	312,9000	0,9895	0,9201
7	275	281,4	244,7	801,1	267,0333	0,7536	0,7852
8	329,7	399	345,6	1074,3	358,1000	1,0643	1,0530
9	476,5	531,8	495,4	1503,7	501,2333	1,5256	1,4738
10	503,6	551	523,2	1577,8	525,9333	1,6112	1,5465
11	408,7	428,1	385,3	1222,1	407,3667	1,1866	1,1978
12	341,8	283	274,2	899	299,6667	0,8444	0,8812
	335,0955	360,4409	324,7182	1020,255	340,0848	-	-

Р

t

ис. 15

Точки, соответствующие индексам сезонности, рассчитанным по данным 2008 года, соединены пунктирной линией, а трем годам – сплошной.

Задача 14. По данным о реализации продукции в 2008 году (см. задачу 11) построить математическую модель указанного ряда динамики.

С учетом долговременных и сезонных факторов, математическая модель ряда динамики представляет собой композицию функцию тренда и индексов сезонности,

.

Используя результаты примера 12, имеем:

.

Задача 15. Смоделировать ряд динамики, характеризующий объем реализации продукции в 2008 году (см. задачу 11) в виде уравнения Фурье. Число гармоник взять равным 1, 2 и 3.

Аналитическим подходом к учету сезонной и долговременной составляющих в ряде динамики, является моделирование его в виде уравнения Фурье (тригонометрического ряда):

.

При этом m – степень точности гармоники тригонометрического ряда; для различных значений m уравнение Фурье выглядит так (на практике берется не более четырех гармоник):

m = 1:
m = 2:
m = 3:

Величина

.

Коэффициенты уравнения Фурье находятся по формулам:

, ,.

Все необходимые вычисления осуществляем в таблицах 14, 15 и 16.

Таблица 14

		m = 1
1	374,6	0	1	0	374,6	0
2	245,5		0,866	0,5	212,6092	122,75
3	304,6		0,5	0,866	152,3	263,7913
4	171,1		0	1	0	171,1
5	210,8		-0,5	0,866	-105,4	182,5582
6	321,3		-0,866	0,5	-278,254	160,65
7	244,7		-1	0	-244,7	0
8	345,6		-0,866	-0,5	-299,2984	-172,8
9	495,4		-0,5	-0,866	-247,7	-429,029
10	523,2		0	-1	0	-523,2
11	385,3		0,5	-0,866	192,65	-333,6796
12	274,2		0,866	-0,5	237,4642	-137,1
	3896,3	-	-	-	-5,7289	-694,9591

Таблица 15

		m = 2
1	374,6	0	1	0	374,6	0
2	245,5		0,5	0,866	122,75	212,6092
3	304,6		-0,5	0,866	-152,3	263,7913
4	171,1		-1	0	-171,1	0
5	210,8		-0,5	-0,866	-105,4	-182,5582
6	321,3		0,5	-0,866	160,65	-278,2540
7	244,7	0	1	0	244,7	0
8	345,6		0,5	0,866	172,8	299,2984
9	495,4		-0,5	0,866	-247,7	429,029
10	523,2		-1	0	-523,2	0
11	385,3		-0,5	-0,866	-192,65	-333,6796
12	274,2		0,5	-0,866	137,1	-237,4642
	3896,3	-	-	-	-179,75	172,7721

Таблица 16

		m = 3
1	374,6	0	1	0	374,6	0
2	245,5		0	1	0	245,5
3	304,6		-1	0	-304,6	0
4	171,1		0	-1	0	-171,1
5	210,8	0	1	0	210,8	0
6	321,3		0	1	0	321,3
7	244,7		-1	0	-244,7	0
8	345,6		0	-1	0	-345,6
9	495,4	0	1	0	495,4	0
10	523,2		0	1	0	523,2
11	385,3		-1	0	-385,3	0
12	274,2		0	-1	0	-274,2
	3896,3	-	-	-	146,2	299,1

Получаем:

,

, ,,

, ,.

Итак, уравнение Фурье в зависимости от числа гармоник имеет следующий вид:

m = 1:
m = 2:	-
m = 3:	-
	+

Задача 16. Результаты задач 14 и 15 изобразить графически. По чертежу определить модель ряда динамики, по которой возможно построить наиболее точный прогноз.

Для того чтобы построить график функции тренда, необходимо подставить в ее уравнения значения t = 1,2, …,12 . Тем самым, для каждого месяца получаем значения . Строим полученную прямую.

Чтобы получить модель ряда динамики, необходимо каждое полученное ранее значение умножить на соответствующий индекс сезонности. Получаем ломаную с вершинами в точках с координатами(t;), .

Для построения графика уравнения Фурье, необходимо для каждого значения t по таблицам 14 – 16 найти значения ,и, которые затем подставляем в уравнение. Получаем . Соединяем отрезками прямых точки с координатами (t; ). Тем самым получаем искомую ломаную.

Все необходимые вычисления удобно производить в таблице 17. Строим чертеж (рисунок 16).

Из рисунка следует, что наиболее точно описывает эмпирические данные модель Фурье, m = 3. Следовательно, по ней возможен наиболее точный прогноз.

Таблица 17

		Линейная модель			Уравнение Фурье
					m = 1	m = 2	m = 3
1	374,6	254,8205	1,1536	293,9650	323,7368	293,7785	318,1452
2	245,5	267,5244	0,7560	202,2592	265,9515	275,9098	325,7598
3	304,6	280,2282	0,9380	262,8664	223,9056	263,8222	239,4556
4	171,1	292,9321	0,5269	154,3513	208,8652	238,8235	188,9735
5	210,8	305,6359	0,6492	198,4122	224,8604	214,9020	239,2687
6	321,3	318,3397	0,9895	314,9887	267,6053	227,6886	277,5386
7	244,7	331,0436	0,7536	249,4667	325,6465	295,6882	271,3215
8	345,6	343,7474	1,0643	365,8530	383,4318	393,3902	343,5402
9	495,4	356,4513	1,5256	543,8130	425,4778	465,3944	489,7611
10	523,2	369,1551	1,6112	594,7987	440,5182	470,4765	520,3265
11	385,3	381,8590	1,1866	453,1014	424,5230	414,5646	390,1980
12	274,2	394,5628	0,8444	333,1785	381,7780	341,8614	292,0114

t

f(t)

Рис. 16

Задача 17. По полученным моделям ряда динамики произвести прогноз реализации продукции в магазине на январь февраль и март 2009 года.

Для того чтобы осуществить прогноз по модели ряда динамики необходимо:

1. определить для прогнозируемого месяца порядковый номер периода от начала отсчета;

2. подставив значение в функцию тренда, найти;

3. по таблице индексов сезонности, найти , соответствующий данному месяцу;

4. умножив на, получить искомый прогноз.

Для того чтобы спрогнозировать значение уровня ряда динамики по уравнению

Фурье, необходимо:

1. для значения найти,,;

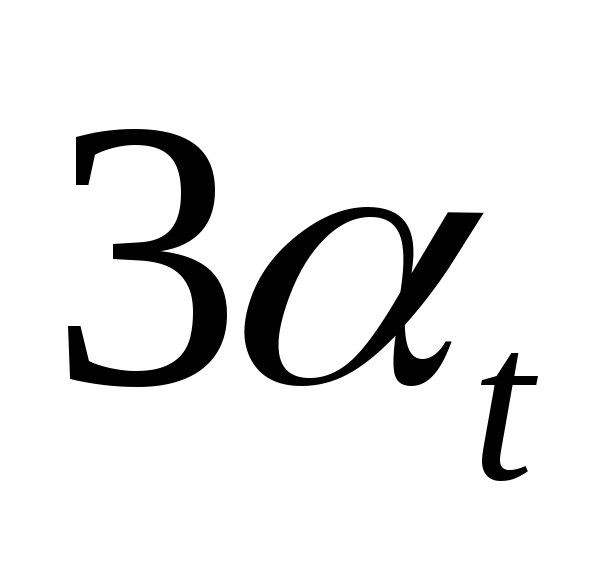2. по таблицам 14 – 16 найти и;

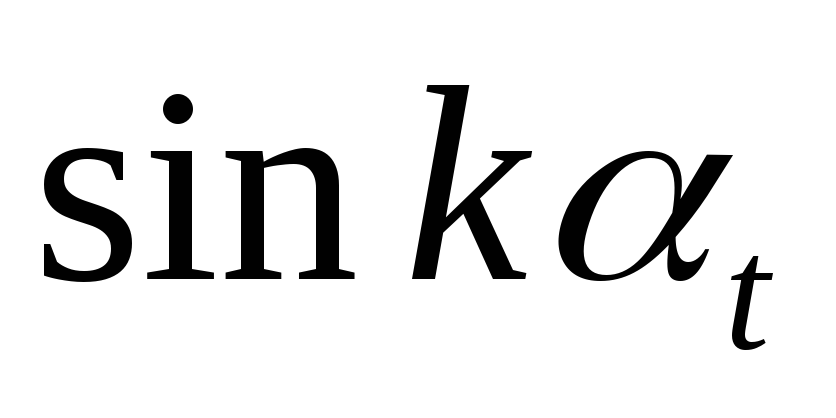3. подставив значения тригонометрических функций в модель Фурье, получить прогнозное значение уровня ряда динамики.

Осуществляем прогноз. Январь, февраль и март 2009 года являются

Соответственно 13, 14 и 15 периодом от начала отсчета (январь 2008 года). Согласно результатам задач 13 и 14 получаем следующие прогнозы:

Январь: (тыс. руб.);

Февраль: (тыс. руб.);

Март: (тыс. руб.).

Прогнозируем объем реализации по модели Фурье:

Январь: ;или

; ;;

; ;;

; ;;

m = 1:(тыс. руб.);

m = 2:(тыс. руб.);

m = 3:

(тыс. руб.);

Февраль: ;или

; ;;

; ;;

; ;;

m = 1:(тыс. руб.);

m = 2:-

(тыс. руб.);

m = 3:

(тыс. руб.);

Март: ;или

; ;;

; ;;

; ;;

m = 1:(тыс. руб.);

m = 2:-

(тыс. руб.);

m = 3:

(тыс. руб.).