2. Отбор факторных признаков, пока модель не построена, производится несколькими способами. Все они основаны на расчете межфакторных коэффициентов корреляции

и парных коэффициентов корреляции

.

Из формул следует, что они находятся точно так же, как и коэффициенты линейной корреляции (см. задачу 9) и обладают аналогичными свойствами.

Способ 1. Этот способ основан на проверке гипотезы о значимости коэффициента линейной корреляции с помощью t – критерия Стьюдента.

Правило проверки гипотезы. Если наблюдаемое значение критерия больше критического,

,

то это с вероятностью γ (уровнем значимости α = 1- γ) говорит о значимости межфакторного коэффициента корреляции , а следовательно о значимости факторного признака (он отбирается в модель). При этом

,

а критическое значение определяется по таблице (см. таблицу 3 Приложения):

, α = 1- γ, ν = n – 2.

Способ 2. Основываясь на свойстве корреляционного отношения, , можно предположить, что чем выше величина межфакторного коэффициента корреляции, тем теснее будет связь между данным факторным и результативным признаком. Таким образом, в модель включаются те из факторных признаков, которым соответствуют наибольшие значения .

Способ 3. Между факторными признаками не должно наблюдаться ни корреляционной, ни тем более функциональной зависимости (в противном случае признаки лишь дублируют друга). Данное условие называется принципом отсутствия автокорреляции. Считается, что между признаками иавтокорреляция отсутствует, если межфакторный коэффициент корреляции

.

Если для факторных признаков это условие нарушается, то один из них необходимо исключить из рассмотрения.

3. Форму и тесноту корреляционной зависимости можно с помощью множественного коэффициента корреляции . В частности, если число факторных признаков равно двум, то

.

Проверкой правильности произведенных расчетов является требование:

.

Если , то связь между признаками линейная. Если же, то связь является линейной и тесной.

4. Проверка статистическое значимости эмпирических данных, а следовательно принципиальная возможность построения регрессионной модели, производится с помощью F – критерия Фишера.

Правило проверки гипотезы. Если наблюдаемое значение критерия больше критического,

,

то это с доверительной вероятностью γ (уровнем значимости α=1- γ) говорит о статистической значимости эмпирических данных. При этом наблюдаемое значение критерия равно

,

а критическое значение критерия определяется по таблице в зависимости от уровня значимости α=1- γ и числа степеней свободы и(см. таблицу 4 Приложения),

.

5. Общий индекс детерминации позволяет определить суммарное влияние факторных признаков на результативный. Он равен:

.

6. После того, как установлена форма корреляционной зависимости, подтверждена гипотеза о статистической значимости эмпирических данных, приступают к построению многофакторной модели регрессии. Например, если модель – линейная, число факторных признаков равно двум, то ее уравнение имеет вид:

.

Параметры модели находятся методом наименьших квадратов путем решения системы нормальных уравнений. Например, в линейном случае для k=2, система имеет вид:

.

Существует другой, упрощенный способ нахождения параметров ,и:

,

,

.

7. Оценка точности регрессионной модели производится также, как и в случае парной регрессии – с помощью средней ошибки аппроксимации (см. задачу 9, п. 7).

8. С помощью дельта – коэффициента можно ответить на вопрос: в какой мере факторный признаквлияет на результативный. Он рассчитывается по формуле:

.

Проверить правильность произведенных расчетов позволяет следующее равенство:

.

9. Величина среднего коэффициента эластичности отвечает на вопрос: на сколько процентов изменится результативный признак, если данный факторный признак изменить на 1%? Он равен:

.

10. С помощью значений дельта – коэффициента и среднего коэффициента эластичности можно исключить из модели самый незначимый признак. Им признается тот, у которого одновременно

, .

Решаем задачу. Вначале, запишем эмпирические данные (объем выборки n=10) в виде таблицы:

	Y
1	4999	5349	420	331
2	6929	6882	553	486
3	6902	7046	570	498
4	10097	7248	883	789
5	8097	5256	433	359
6	11116	14090	839	724
7	4880	3525	933	821
8	7355	5431	526	428
9	10066	7680	676	607
10	7884	8226	684	619

Все необходимые расчеты осуществлены в таблице 12. Под таблицей рассчитаем средние значения, дисперсии (по формуле разностей) и средние квадратические отклонения каждого из признаков.

Таблица 12

	у
1	4999	24990001	5349	28611801	26739651	420	176400	2099580	331	109561	1654669	2246580	1770519	139020
2	6929	48011041	6882	47361924	47685378	553	305809	3831737	486	236196	3367494	3805746	3344652	268758
3	6902	47637604	7046	49646116	48631492	570	324900	3934140	498	248004	3437196	4016220	3508908	283860
4	10097	101949409	7248	52533504	73183056	883	779689	8915651	789	622521	7966533	6399984	5718672	696687
5	8097	65561409	5256	27625536	42557832	433	187489	3506001	359	128881	2906823	2275848	1886904	155447
6	11116	123565456	14090	198528100	156624440	839	703921	9326324	724	524176	8047984	11821510	10201160	607436
7	4880	23814400	3525	12425625	17202000	933	870489	4553040	821	674041	4006480	3288825	2894025	765993
8	7355	54096025	5431	29495761	39945005	526	276676	3868730	428	183184	3147940	2856706	2324468	225128
9	10066	101324356	7680	58982400	77306880	676	456976	6804616	607	368449	6110062	5191680	4661760	410332
10	7884	62157456	8226	67667076	64853784	684	467856	5392656	619	383161	4880196	5626584	5091894	423396
	78325	653107157	70733	572877843	594729518	6517	4550205	52232475	5662	3478174	45525377	47529683	41402962	3976057

Y: , ,

, .

: , ,

, .

: , ,

, .

: , ,

, .

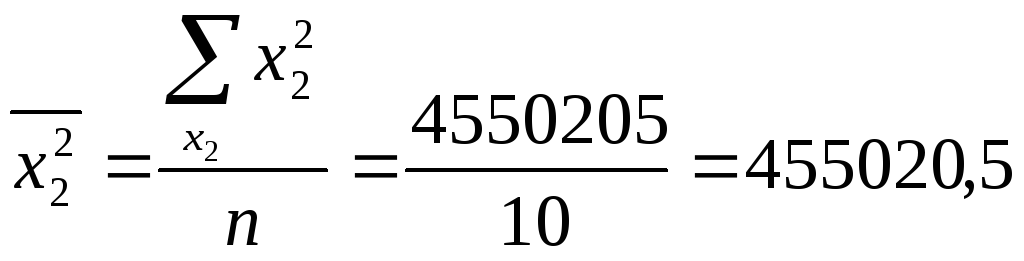Теперь найдем средние значения произведений признаков:

;

;

;

;

;

;

.

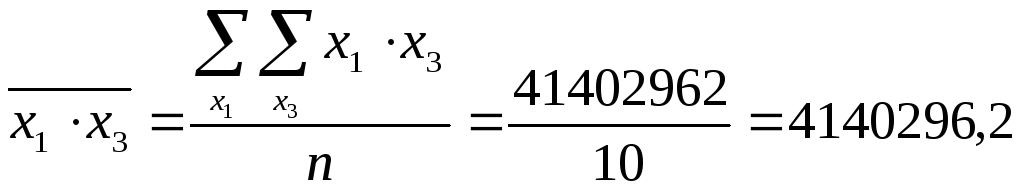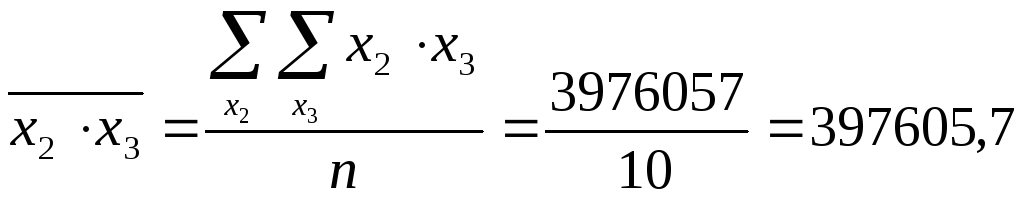Вычисляем межфакторные и парные коэффициенты линейной корреляции:

,

;

,

;

,

;

,

;

,

;

,

.

Займемся отбором факторных признаков в модель.

Сначала с вероятностью 0,95 оценим статистическую значимость каждого из имеющихся факторных признаков. Согласно таблице 3 приложения критическое значение критерия Стьюдента для уровня значимости

α = 1 - 0,95 = 0,05 и числа степеней свободы ν =10 – 2 = 8 равно

.

Вычислим наблюдаемые значения:

: ;

: ;

: .

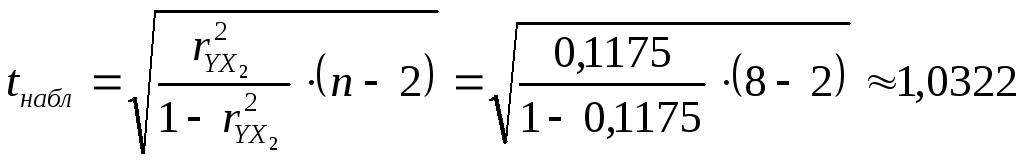Видим, что только для признака выполняется правило проверки гипотезы. Следовательно, он однозначно включается в модель.

Между признаками инарушается принцип отсутствия автокорреляции,, связь между ними тесная. Поэтому, один из этих признаков подлежит исключению. Поскольку>, то признакисключается из рассмотрения, а признак- остается.

Множественный коэффициент корреляции равен:

Найденное значение указывает на высокую степень тесноты и линейности корреляционной зависимости.

С вероятностью 0,95 выдвинем гипотезу о статистической значимости эмпирических данных. Поскольку n = 10, k =2, то α=1- 0,95 = 0,05 ,. Согласно таблице 4

.

Наблюдаемое значение равно:

.

Правило проверки гипотезы выполнено. Поэтому с вероятностью 0,95 гипотеза о статистической значимости эмпирических данных принимается, корреляционная модель может быть построена.

Общий индекс детерминации равен

.

Следовательно, факторные признаки, отобранные в модель, влияют на

результативный в пределах 59,43%. Это не очень сильное влияние. Согласно закону Парето степень влияния должна быть не меньше 80%.

Линейная модель, описывающая корреляционную зависимость, имеет следующий общий вид:

.

Используя таблицу 12, получаем систему нормальных уравнений:

; .

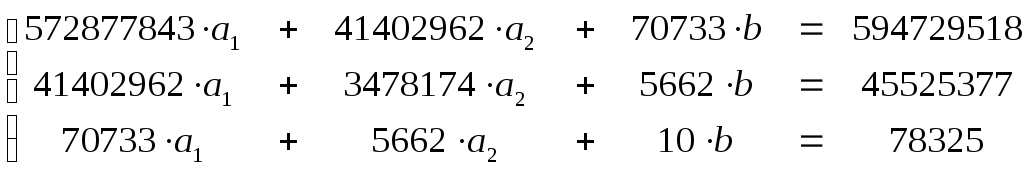Решая систему, получаем:

, ,.

Итак, искомое уравнение регрессии имеет вид:

.

Найдем параметры уравнения регрессии упрощенным способом:

,

.

Найдем среднюю ошибку аппроксимации. Для этого, подставив значения факторных признаков, соответствующих данному значению y в модель, получаем теоретические значения y* . Вычисления производим в таблице:

у
4999	5349	331	6672,0838	0,3347
6929	6882	486	7708,8693	0,1126
6902	7046	498	7824,4743	0,1337
10097	7248	789	8461,0588	0,1620
8097	5256	359	6644,8366	0,1793
11116	14090	724	12009,5096	0,0804
4880	3525	821	6574,3001	0,3472
7355	5431	428	6894,8649	0,0626
10066	7680	607	8339,5446	0,1715
7884	8226	619	8642,1934	0,0962
	-	-	-	1,6801

Итак, значение средней ошибки аппроксимации равно

,

что говорит о низкой точности модели.

Определим значения дельта – коэффициентов. Имеем:

или 91,54%,

или 8,46%.

Сумма дельта – коэффициентов равна 1, следовательно, есть все основания полагать, что вычисления произведены верно. Итак, признак влияет на признак Y в пределах 91,54%, а степень влияния признака равна 8,46%.

Найдем величины средних коэффициентов эластичности:

или 47,82%,

или 12,23%.

Таким образом, изменение признака на 1% влечет за собой изменение признакаY на 47,82%, а вследствие изменения признака , изменение признакаY составит 12,23%

Перейдем к модели с парной регрессией. Поскольку одновременно минимум дельта – коэффициента и среднего коэффициента эластичности соответствует признаку ,

,

,

то он исключается из модели. Итак, общий вид уравнения парной регрессии следующий:

.

Так как , то согласно выводам задачи 9 связь признается линейной и тесной. Уравнение прямой линии регрессии найдем упрощенным способом (смотри п. 6 задачи 9):;

;

;

.