
лекции / Л7пересечен прям с конус и цилиндр2019 ред
.pdf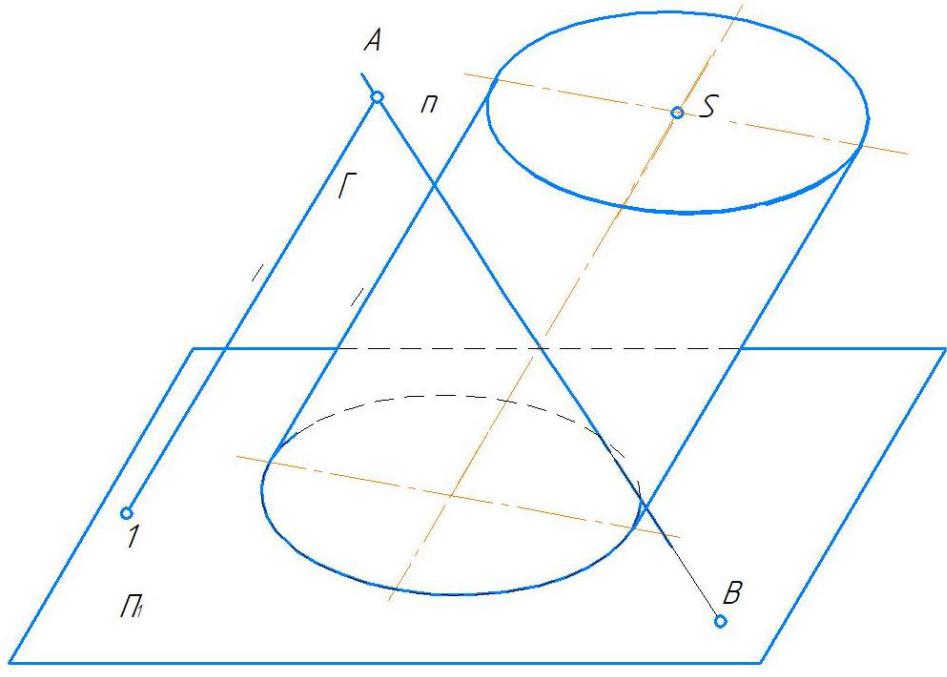
21
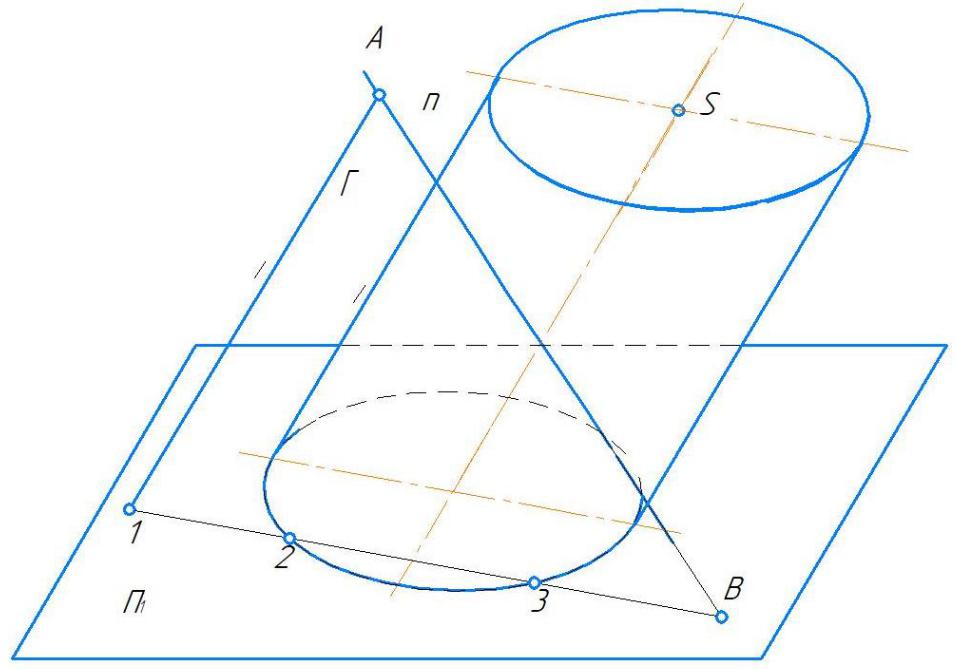
2 проводим прямую1B – линию пересечения плоскости Γ с П1; 3 определяем точки 2 и 3 – точки пересечения
плоскости Γ с основанием цилиндра;
22
23
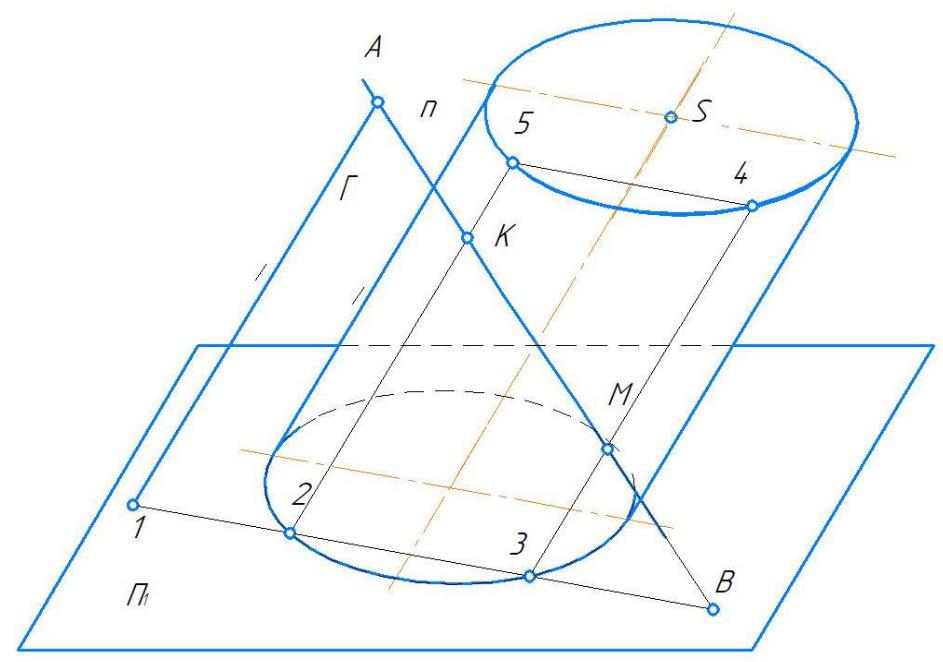
4 строим образующие 25 и 34, по которым плоскость Γ пересекает цилиндр;
5 определяем точки K и M пересечения прямой n с образующими.
24
25
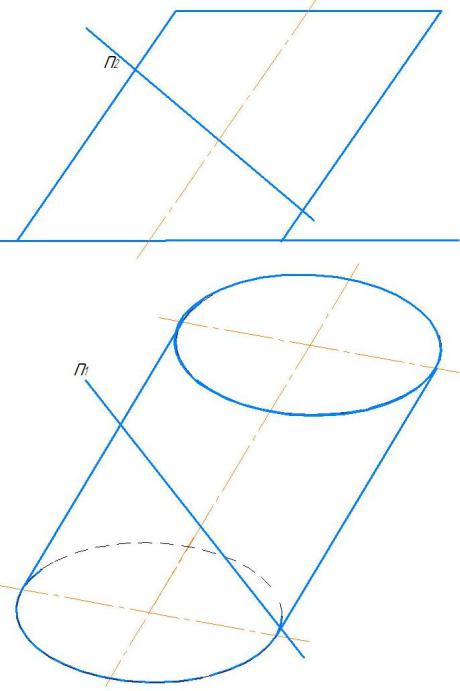
Построения на комплексном чертеже:
26
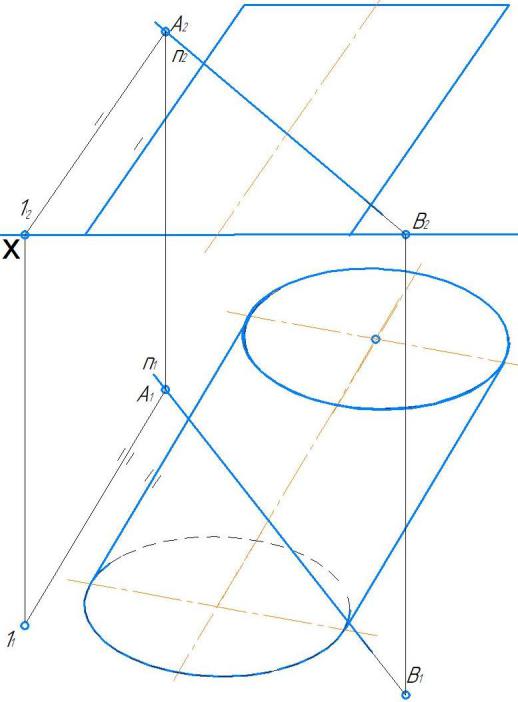
1 продлеваем n2 до
пересечения с осью x
в ( )B2.
2 по линии связи на n1 находим ( )B1.
3 через произвольную ( )A2 на n2 проводим прямую параллельную фронтальной проекции оси цилиндра до
пересечения с осью x
в ( )12.
4 по линии связи на n1 находим ( )A1; 27
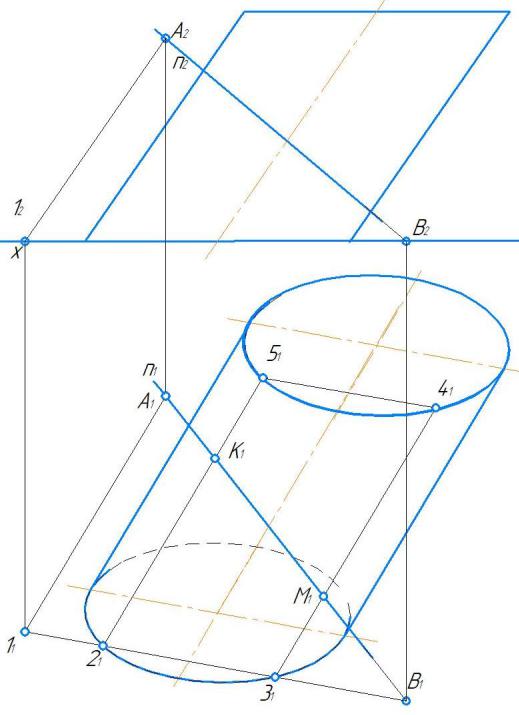
5через ( )A1 проводим прямую, параллельную горизонтальной проекции оси цилиндра до пересечения с линией связи ( )12 - получим ( )11;
6проводим прямую 11B1 – линию пересечения плоскости Γ с П1. Точки 21 и 31 – точки пересечения плоскости Γ с основанием цилиндра.
7проводим через эти точки образующие цилиндра
2151 и 3141. Точки пересечения этих образующих с прямой n и будут общими точками цилиндра и прямой, то есть точками их пересечения. ( )K1 на
2151, ( )M1 на 3141.
28
29
8 по линиям связи находим ( )K2 и ( )M2 на n2.
Видимость можно определить используя метод конкурирующих точек.
30
