
лекции / Л1-3 НГ (1)
.pdfИНЖЕНЕРНАЯ ГРАФИКА
1
ВВЕДЕНИЕ
Начертательная геометрия (НГ) – это один из разделов геометрии, в котором пространственные фигуры, состоящие из точек, линий и поверхностей, изучаются по их проекционным отображениям.
Одной из основных задач НГ является создание
Метода отображения трехмерных фигур на плоскость и разработка способов решения позиционных и метрических задач по плоскостным отображениям этих фигур.
2
НГ способствует развитию у человека пространственного воображения, без которого невозможно никакое инженерное творчество.
НГ составляет теоретическую базу для построения чертежа.
Чертеж – это своебразный язык, с помощью которого, используя всего лишь точки, линии и ограниченное число геометрических знаков и цифр, можно изобразить на плоскости сложные приборы, машины и инженерные сооружения.
Причем этот графический язык интернационален, он понятен любому технически грамотному человеку, независимо от того на каком языке он говорит.
3
ТОЧКА
Точка относится к основным, неопределяемым понятиям геометрии. Она не может быть определена другими более элементарными понятиями.
Точка не имеет размеров. То, что мы показываем на чертеже точку в виде какой-то площадки, пересечения двух линий или кружочком, является лишь условным ее изображением.
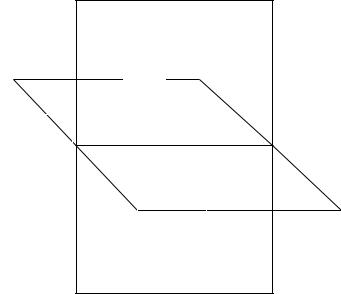
Возьмем две взаимно-перпендикулярные плоскости. Примем их за плоскости проекций. Горизонтальную плоскость обозначим Π1 (H), вертикальную плоскость обозначим Π2 (V) – ее называют
фронтальной плоскостью проекций. |
4 |
|
II |
Π2 |
|
I |
x |
|
III |
Π1 |
|
IV |
Линия пересечения плоскостей проекций называется осью проекций.
Обозначается буквой x c индексами, соответствующими номерам плоскостей проекций – в нашем случае x12.
Плоскости проекций делят пространство на 4 четверти.
5
Π2 |
А |
|
2 |
|
А |
x |
Аx |
|
|
Π1 |
А1 |
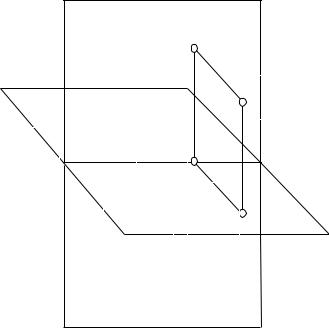
Возьмем точку А в первой четверти. Опустим из нее перпендикуляры на плоскости Π1 и Π2. Точки пересечения перпендикуляров с плоскостями проекций и будут горизонтальной А1 и фронтальной А2 проекциями точки А. Для обозначения прекций точек используют большие буквы латинского алфавита (A,B,C,D…) или для вспомогательных точек при решении задач - арабские цифры с индексами, соответствующими номеру плоскости проекций. 6
Проецирующие прямые АА1 и АА2, соответственно перпендикулярные Π1 и Π2, определяют плоскость, перпендикулярную плоскостям проекций и линии их пересечения – оси x. Эта плоскость в пересечении с Π1 и Π2 образует две взаимно перпендикулярные прямые А1Ах и А2Ах, пересекающиеся в точке Ах на оси проекций. Значит, проекции точки будут лежать на прямых, перпендикулярных оси проекций и пересекающих эту ось в одной и той же точке.
7
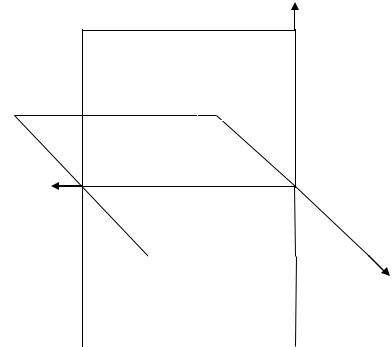
Если известны две проекции |
|
|
Z |
точки А1 и А2, то, построив из |
|
|
|
|
Π2 |
|
|
них перпендикуляры к плос- |
|
-Y |
|
|
|
||
костям проекций, получим в |
|
|
|
пересечении этих перпенди- |
|
|
|
куляров точку А. |
X |
|
Π1 |
|
|
|
То есть, две проекции точки |
|
|
|
|
Y |
||
определяют ее положение в |
|
||
|
|
||
пространстве относительно |
|
|
Z |
|
- |
||
данной системы плоскостей |
|
|
|
проекций. |
|
|
|
Введем систему координат XYZ, как показано на
рисунке. |
8 |

Положение точки в пространстве определяется однозначно тремя координатами x,y,z. Если мы сможем отобразить эти три координаты на плоскости, мы сможем работать не с пространственными объектами, а с их двухмерными образами.
|
Π2 |
А |
Π2(Π1) |
А2 |
-Y |
z |
|
|
|
|
|||
|
|
2 |
|
|
|
|
|
ZA |
XA |
А |
ZA |
XA |
|
x |
Аx |
x |
Аx |
|
||
|
|
|
||||
|
Π1 |
YA |
А1 |
YA |
|
|
|
|
|
|
|
А1 |
|
|
|
|
|
|
Y |
-z |
9

Французский ученый Гаспар Монж (1746-1818) предложил такой алгоритм перехода от пространства к плоскости: повернем плоскость Π1 вокруг оси x, так чтобы положительная полуплоскость Π1 совместилась с отрицательной полуплоскостью Π2; при этом другая половина Π1 пойдет вверх и совпадет с верхней полуплоскостью Π2.
Мы получили на плоскости две проекции точки А - А1 и А2. При этом сохранились все три координаты точки.
10
