8363_НерсисянАС_ПР-6
.docx
МИНОБРНАУКИ РОССИИ
Санкт-Петербургский государственный
электротехнический университет
«ЛЭТИ» им. В.И. Ульянова (Ленина)
Кафедра информационных систем
отчет
по практической работе №6
по дисциплине «Теория информации»
Тема: Эффективное кодирование. Код Хаффмана.
Студент гр. 8363 |
|
Нерсисян А.С. |
Преподаватель |
|
Писарев И.А. |
Санкт-Петербург
2020
Цель работы
Изучить основную теорему Хаффмана о эффективном кодировании и решить задачи по данной теме.
Задание на практическую работу
2.1. Письменно ответить на вопросы
Опишите метод Хаффмана.
Какие существуют другие методы кодирования? Дайте их сравнитель-ную характеристику.
2.2. Решить задачи
Закодировать сообщение методом Хаффмана.
сообщение |
1 |
2 |
3 |
4 |
5 |
6 |
7 |
вероятность |
0,3 |
0,2 |
0,2 |
0,1 |
0,1 |
0,05 |
0,05 |
Алфавит содержит 7 букв, которые встречаются с вероятностями 0,4; 0,2; 0,1; 0,1; 0,1; 0,05; 0,05. Осуществите кодирование по методу Хаффмана.
Выполнение работы
Опишите метод Хаффмана.
Суть метода кодирования Хаффмана заключается в следующем:
1.Взять два наименее вероятных символа в алфавите. Эти два символа получат кодовые слова с максимальной длиной, отличающиеся последним символом.
2. Объединить два символа в один, повторить 1.
Кодируемые знаки располагают в порядке убывания их вероятностей. Далее на каждом этапе две последние позиции списка заменяются одной и ей приписывают вероятность, равную сумме вероятностей заменяемых позиций. После этого производится пересортировка списка по убыванию вероятностей, с сохранением информации о том, какие именно знаки объединялись на каждом этапе. Процесс продолжается до тех пор, пока не останется единственная позиция с вероятностью, равной 1.
После этого строится кодовое дерево. Корню дерева ставится в соответствие узел с вероятностью, равной 1. Далее каждому узлу приписываются два потомка с вероятностями, которые участвовали в формировании значения вероятности обрабатываемого узла. Так продолжают до достижения узлов, соответствующих вероятностям исходных знаков. Процесс кодирования по кодовому дереву осуществляется следующим образом. Одной из ветвей, выходящей из каждого узла, например, с более высокой вероятностью, ставится в соответствие символ 1, а с меньшей - 0. Спуск от корня к нужному знаку дает код этого знака.
Какие существуют другие методы кодирования? Дайте их сравнительную характеристику.
Кодирование Шеннона
Кодирование Шеннона-Фано
Блочное кодирование
Арифметическое кодирование
Методика Шеннона–Фано не всегда приводит к однозначному построению кода.
Ведь при разбиении на подгруппы на 1-й итерации можно сделать большей по вероятности как верхнюю, так и нижнюю подгруппу. В результате среднее число символов на букву окажется другим.
Таким образом, построенный код может оказаться не самым лучшим.
От указанного недостатка свободна методика Хаффмана. Она гарантирует однозначное построение кода с наименьшим для данного распределения вероятностей средним числом символов на букву.
Метод Хаффмана производит идеальное сжатие (то есть, сжимает данные до их энтропии), если вероятности символов точно равны отрицательным степеням числа 2. Результаты эффективного кодирования по методу Хаффмана всегда лучше результатов кодирования по методу Шеннона-Фано.
Блочное кодирование работает почти также, как и метод Хаффмана, только вместо символов кодируются группа (блок, в некоторых случаях – слова) символов. Оно эффективно, если величина среднего числа символов на знак оказывается значительно большей, чем энтропия, это говорит об избыточности кода. Эту избыточность можно устранить, если перейти к кодированию блоками.
Арифметическое кодирование — алгоритм сжатия информации без потерь. Данный метод, как и алгоритм Хаффмана, является энтропийным, т.е. длина кода конкретного символа зависит от частоты встречаемости этого символа в тексте. Арифметическое кодирование показывает более высокие результаты сжатия, чем алгоритм Хаффмана, для данных с неравномерными распределениями вероятностей кодируемых символов. Кроме того, при арифметическом кодировании каждый символ кодируется нецелым числом бит, что эффективнее кода Хаффмана.
2.2. Решить задачи
Закодировать сообщение методом Хаффмана.
сообщение |
1 |
2 |
3 |
4 |
5 |
6 |
7 |
вероятность |
0,3 |
0,2 |
0,2 |
0,1 |
0,1 |
0,05 |
0,05 |
|
|
Построение дерева вероятностей |
Итоговый код |
|||||
1 |
0.3 |
0.3 |
0.3 |
0.3 |
0.4 |
0.6 |
1 |
11 |
2 |
0.2 |
0.2 |
0.2 |
0.3 |
0.3 |
0.4 |
|
01 |
3 |
0.2 |
0.2 |
0.2 |
0.2 |
0.3 |
|
|
00 |
4 |
0.1 |
0.1 |
0.2 |
0.2 |
|
|
|
100 |
5 |
0.1 |
0.1 |
0.1 |
|
|
|
|
1011 |
6 |
0.05 |
0.1 |
|
|
|
|
|
10101 |
7 |
0.05 |
|
|
|
|
|
|
10100 |

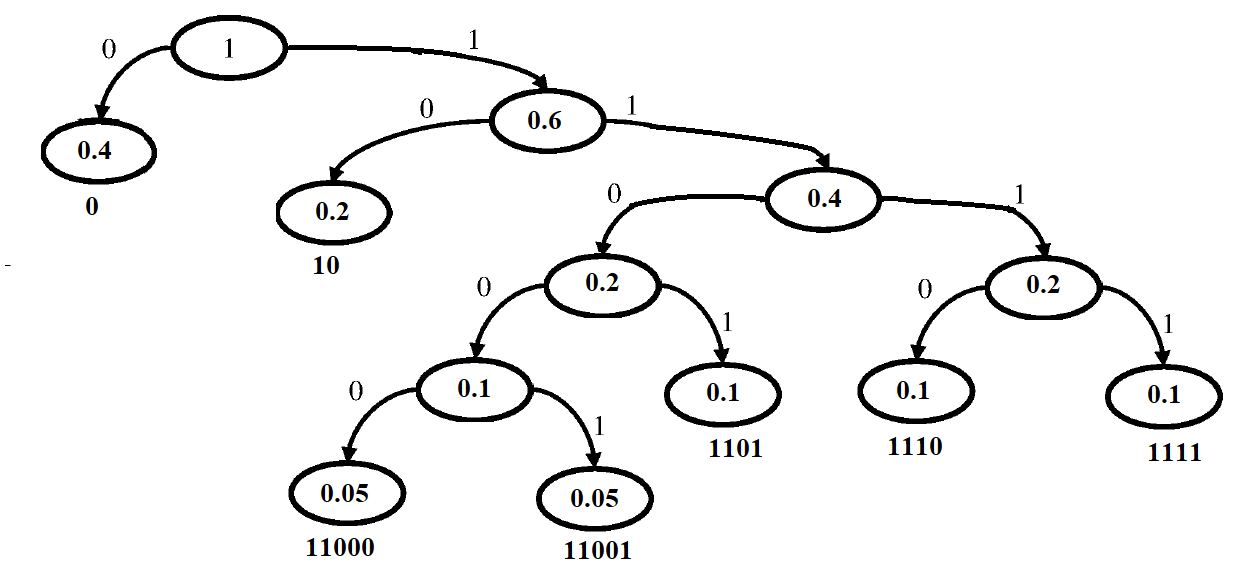
Алфавит содержит 7 букв, которые встречаются с вероятностями 0,4; 0,2; 0,1; 0,1; 0,1; 0,05; 0,05. Осуществите кодирование по методу Хаффмана.
|
|
Построение дерева вероятностей |
Итоговый код |
|||||
|
0.4 |
0.4 |
0.4 |
0.4 |
0.4 |
0.6 |
1 |
0 |
|
0.2 |
0.2 |
0.2 |
0.2 |
0.4 |
0.4 |
|
10 |
|
0.1 |
0.1 |
0.2 |
0.2 |
0.2 |
|
|
1111 |
|
0.1 |
0.1 |
0.1 |
0.2 |
|
|
|
1110 |
|
0.1 |
0.1 |
0.1 |
|
|
|
|
1101 |
|
0.05 |
0.1 |
|
|
|
|
|
11001 |
|
0.05 |
|
|
|
|
|
|
11000 |
СПИСОК ИСПОЛЬЗОВАННЫХ ИСТОЧНИКОВ
Гошин Е.В. Теория информации и кодирования: учеб, пособие / Е.В. Гошин – Самара: Изд-во Самарского университета, 2018. - 124 с.