
8363_НерсисянАС_ПР-4
.docx
МИНОБРНАУКИ РОССИИ
Санкт-Петербургский государственный
электротехнический университет
«ЛЭТИ» им. В.И. Ульянова (Ленина)
Кафедра информационных систем
отчет
по практической работе №4
по дисциплине «Теория информации»
Тема: Основы теории кодирования. Код Хемминга
Студент гр. 8363 |
|
Нерсисян А. С. |
Преподаватель |
|
Писарев И. А. |
Санкт-Петербург
2020
Цель работы
Изучить основы теории кодирования и кода Хемминга.
Задание на практическую работу
2.1. Письменно ответить на вопросы
Какие элементы содержатся в общей схеме передачи информации?
Сформулируйте задачу надёжной передачи сообщений.
Объясните, почему кодирование с контрольной суммой позволяет обнаружить в процессе передачи только нечётное число ошибок?
В чем заключается способ построения кодов с исправлением ошибки?
Дайте определение расстояния Хемминга между двоичными словами.
2.2. Решить задачи
1.
Для слов длины
 в алфавите
в алфавите
 используются кодовые слова длины
используются кодовые слова длины
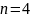 (3, 4 – коды). Порождающая матрица
(3, 4 – коды). Порождающая матрица
 имеет вид:
имеет вид:

Какую по кратности ошибку может обнаружить этот код?
a) Определите
кодовое слово
 для слова исходного сообщения
для слова исходного сообщения
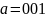 .
.
b) Какое кодовое
слово
соответствует слову исходного сообщения
 .
.
c) Какое кодовое
слово
соответствует слову исходного сообщения
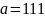 .
.
2.
Для слов длины
 в алфавите
используются кодовые слова длины
в алфавите
используются кодовые слова длины
 (2, 6 – коды). Порождающая матрица
(2, 6 – коды). Порождающая матрица
 имеет вид:
имеет вид:

Какую по кратности ошибку может обнаружить этот код?
a) Определите
кодовое слово
для слова исходного сообщения
 .
.
b) Какое кодовое
слово
соответствует слову исходного сообщения
 .
.
c) Какое кодовое
слово
соответствует слову исходного сообщения
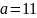 .
.
Выполнение работы
2.1
1. Структура процесса передачи данных.

Источник информации
Приёмник информации


Канал связи
Декодирующее устройство
Кодирующее устройство

Помехи
Сформулируйте задачу надёжной передачи сообщений.
Задача надежной передаче информации заключается в восстановлении, по искаженным словам, реально отправленных слов.
При кодировании с контрольной суммой используется так называемый разряд четности. Последний символ кода равен сумме всех предыдущих по
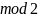 .
При нечетном числе ошибок контрольная
сумма позволяет обнаружить факт ошибки,
а при четном числе ошибок символ кода
будет таким же, как и при отсутствии
ошибок, потому что она считается как
сумма всех предыдущих разрядов по
.
.
При нечетном числе ошибок контрольная
сумма позволяет обнаружить факт ошибки,
а при четном числе ошибок символ кода
будет таким же, как и при отсутствии
ошибок, потому что она считается как
сумма всех предыдущих разрядов по
.
В чем заключается способ построения кодов с исправлением ошибки.
Способ построения кодов и исправлением ошибки заключается в повторении каждого символа некоторое количество раз, таким образом каждый символ можно достоверно декодировать даже если в его коде символы различны. Чем больше раз повторяется символ, тем выше шанс правильного исправления ошибки при сильных помехах.
Пусть
 и
и
 – двоичные слова длины
– двоичные слова длины
 в алфавите
в алфавите
 .
Расстояние Хемминга
.
Расстояние Хемминга
 между
и
между
и
 следующим образом:
следующим образом:
 равно числу несовпадений в соответствующих
позициях слов
и
.
равно числу несовпадений в соответствующих
позициях слов
и
.
Функция удовлетворяет всем аксиомам расстояния:
1.
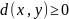 ,
причём
,
причём
 только при
только при
 ;
;
2.
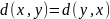 ;
;
3.
 – неравенство треугольника
– неравенство треугольника
2.2. Решить задачи
1. Для слов длины в алфавите используются кодовые слова длины (3, 4 – коды). Порождающая матрица имеет вид:
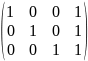
Какую по кратности ошибку может обнаружить этот код?
Данный код способен обнаруживать однократную ошибку
Четвёртый символ кодовых слов – контрольный: он будет равен 0, если исходное слово содержит чётное число единиц, и будет равен 1 в противном случае.
Определите кодовое слово для слова исходного сообщения .
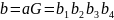 где
где




кодовое слово для
слова исходного сообщения
будет
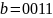
Какое кодовое слово соответствует слову исходного сообщения .
где

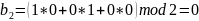


кодовое слово для
слова исходного сообщения
будет

Какое кодовое слово соответствует слову исходного сообщения .
где




кодовое слово для
слова исходного сообщения
будет

2. Для слов длины в алфавите используются кодовые слова длины (2, 6 – коды). Порождающая матрица имеет вид:
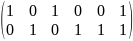
Какую по кратности ошибку может обнаружить этот код?
Данный код способен обнаруживать двухкратную ошибку.
Определите кодовое слово для слова исходного сообщения .
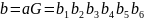 где
где
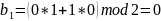


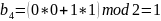


кодовое слово для
слова исходного сообщения
будет

Какое кодовое слово соответствует слову исходного сообщения .
где




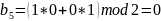

кодовое слово для
слова исходного сообщения
будет
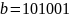
Какое кодовое слово соответствует слову исходного сообщения .
где




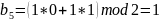

кодовое слово для
слова исходного сообщения
будет
СПИСОК ИСПОЛЬЗОВАННЫХ ИСТОЧНИКОВ
Гошин Е.В. Теория информации и кодирования: учеб, пособие / Е.В. Гошин – Самара: Изд-во Самарского университета, 2018. - 124 с.
Луковкин С.Б. Теоретические основы информатики: учеб. пособие / С.Б. Луковкин – Мурманск: Изд-во МГТУ, 2008. - 125 с.
