8363_НерсисянАС_ПР-2
.docx
МИНОБРНАУКИ РОССИИ
Санкт-Петербургский государственный
электротехнический университет
«ЛЭТИ» им. В.И. Ульянова (Ленина)
Кафедра информационных систем
отчет
по практической работе №2
по дисциплине «Теория информации»
Тема: Количество информации. Формула Хартли. Формула Шеннона.
Студент гр. 8363 |
|
Нерсисян А. С. |
Преподаватель |
|
Писарев И. А. |
Санкт-Петербург
2020
Цель работы
Изучить понятия количество информации, состояние системы, энтропия, формулы Хартли и Шеннона.
Задание на практическую работу
2.1. Письменно ответить на вопросы
Формула измерения количества информации Р. Хартли.
Единицы измерения количества информации.
Понятие информационной энтропии. Единицы измерения энтропии.
Развитие теории информации в работах Клода Шеннона. Формула Шеннона.
Связь понятий «количество информации-состояние системы-энтропия».
2.2. Решить задачи
2.2.1. Привести пример вычисления формулы Хартли для определения числа вопросов в задаче угадывания задуманного числа из заданного интервала (например, 1-32, 1-100). Представить вопросы и ответы для данного примера.
2.2.2. Получены три различных сообщения A, B, C: A=«начало конференции в девять часов»; B=«начало конференции в девять часов в понедельник»; C=«начало конференции ровно в девять часов». Используя энтропийный подход Шеннона, сравнить количество информации, содержащееся в этих сообщениях. Записать формулой.
2.2.3. Придумать свой пример сравнения количества информации, аналогичный предыдущей задаче.
2.2.4.
Определить количество информации в
сообщении по формуле Шеннона, если число
символов алфавита источника
,
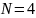вероятности появления символов источника
и
.
Выполнение работы
Формула измерения количества информации Р. Хартли.
Количество
информации при наблюдении случайной
величины
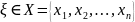с распределением вероятностей
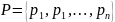при
задается
формулой Хартли:
.
Единицы измерения количества информации.
Базовой единицей измерения количества информации является бит, который представляет собой количество информации, получаемое при наблюдении случайной величины, имеющей два равновероятных значения.
Понятие информационной энтропии. Единицы измерения энтропии.
Информационная энтропия – это мера неопределённости состояния некоторой случайной величины (физической системы) с конечным или счётным числом состояний.
При
случайной величине
,
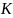которая может принимать
различных
значений
,
и если все значения этой случайной
величины
равновероятны, то энтропия (мера
неопределённости) величины
будет равна:
.
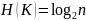Энтропия и количество информации измеряются в одних и тех же единицах – в битах.
Развитие теории информации в работах Клода Шеннона. Формула Шеннона.
Клод
Шеннон, используя подход Р. Хартли,
обратил внимание на то, что при передаче
словесных сообщений частота (вероятность)
использования различных букв алфавита
не одинакова: некоторые буквы используются
очень часто, другие - редко. Он определил,
что с алфавитом
состоящих из
символов, в
передаваемом сообщении длиной
символов, один
ый символ алфавита несёт количество
информации равное
.
Учитывая
вышесказанное, общее количество
информации,
содержащееся в сообщении из
символов равно:
Количество
энтропии
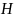произвольной системы
(случайной
величины), которая может находиться в
различных состояниях
c вероятностями
, вычисленное по
формуле Шеннона,
равно
Связь понятий «количество информации - состояние системы - энтропия».
Энтропия
характеризует степень неопределённости
системы. Максимум энтропии
достигается в том случае, когда все
состояния системы равновероятны. Если
система
может находиться только в одном состоянии
,
то её энтропия равна нулю. Среди систем,
которые могут принимать только два
состояния, наибольшая энтропия будет
у системы с равновероятными состояниями.
Чем больше объём полученных о системе
сведений, тем больше будет информации
о системе. Если энтропия системы после
получения информации становится равной
нулю, это означает, что неопределённость
исчезла, вся энтропия «перешла» в
информацию. В этом случае была получена
полная информация о системе
.
Количество информации, приобретаемое
при полном выяснении состояния физической
системы, равно энтропии этой системы.
Если после получения некоторого сообщения
неопределённость системы X стала меньше,
но не исчезла совсем, то количество
информации, содержащееся в сообщении,
равно приращению энтропии:
,
где
и
- энтропия системы до и после сообщения,
соответственно.
2.2.1. Привести пример вычисления формулы Хартли для определения числа вопросов в задаче угадывания задуманного числа из заданного интервала (например, 1-32, 1-100). Представить вопросы и ответы для данного примера.
Решение.
Выберем
интервал 1-64. По формуле Хартли вычислим
количество информации, которое необходимо
получить для определения выделенного
элемента
из множества целых чисел {1,2,3 ……, 64}.
Для
этого необходимо получить
бит информации.
Пусть, задумано число 53.
Вопрос №1: Задуманное число принадлежит множеству {33 … 64}?
Ответ «да» приносит 1 бит информации.
Вопрос №2: Задуманное число принадлежит множеству {33 … 48}?
Ответ «нет», значит число принадлежит множеству {49 ... 64}.
Вопрос №3: Задуманное число принадлежит множеству {57 … 64}?
Ответ «нет».
Вопрос №4: Задуманное число принадлежит множеству {49 … 52}?
Ответ «нет».
Вопрос №5: Задуманное число принадлежит множеству {55 … 56}?
Ответ «нет».
Вопрос №6: Задуманное число равно 53?
Ответ «да»
2.2.2. Получены три различных сообщения A, B, C: A = «начало конференции в девять часов»; B = «начало конференции в девять часов в понедельник»; C = «начало конференции ровно в девять часов». Используя энтропийный подход Шеннона, сравнить количество информации, содержащееся в этих сообщениях. Записать формулой.
Решение:
Обозначим количество информации в сообщениях A, B, C через I(A), I(B), I(C) соответственно. Все символы сообщения А содержатся в сообщении B и С, сообщение С = A + «ровно», В = A + «в понедельник», в соответствии с подходом Шеннона получаем: I(A) < I(C) < I(B).
2.2.3. Придумать свой пример сравнения количества информации, аналогичный предыдущей задаче.
Решение:
Получены сообщения A, B, C:
A = «карантин закончится»;
B = «карантин закончится в ноябре»;
C = «карантин закончится в ноябре 2150 года».
Обозначим количество информации в сообщениях A, B, C через I(A), I(B), I(C) соответственно.
Сообщение А содержится и в В и в С;
В = А + «в ноябре»; С = В + «2150 года».
в соответствии с подходом Шеннона получаем: I(A) < I(B) < I(C).
2.2.4. Определить количество информации в сообщении по формуле Шеннона, если число символов алфавита источника , вероятности появления символов источника и .
Решение:
СПИСОК ИСПОЛЬЗОВАННЫХ ИСТОЧНИКОВ
Зверева Е.Н., Лебедько Е.Г. Сборник примеров и задач по основам теории информации и кодирования сообщений: СПб: НИУ ИТМО, 2014. - 76 с.
Луковкин, С.Б. Теоретические основы информатики: учеб. пособие / С.Б. Луковкин – Мурманск: Изд-во МГТУ, 2008. - 125 с.