31.Сопротивление в цепи синусоидального тока

      Если напряжение подключить к сопротивлению R, то через него протекает ток

     (6.7)

     Анализ выражения (6.7) показывает, что напряжение на сопротивлении и ток, протекающий через него, совпадают по фазе.         Формула (6.7) в комплексной форме записи имеет вид

     (6.8)

      где и- комплексные  амплитуды  тока и напряжения.      Комплексному уравнению (6.8) соответствует векторная диаграмма (рис. 6.4).

     Из анализа диаграммы следует, что векторы напряжения и тока совпадают по направлению.      Сопротивление участка цепи постоянному току называется омическим, а сопротивление того же участка переменному току - активным сопротивлением.                                Рис.6.4      Активное сопротивление больше омического из-за явления поверхностного эффекта. Поверхностный эффект заключается в том, что ток вытесняется из центральных частей к периферии сечения проводника.

6.5. Индуктивная катушка в цепи синусоидального тока

     Сначала рассмотрим идеальную индуктивную катушку, активное сопротивление которой равно нулю. Пусть по идеальной катушке с индуктивностью L протекает синусоидальный ток . Этот ток создает в индуктивной катушке переменное магнитное поле, изменение которого вызывает в катушке ЭДС самоиндукции

     (6.9)

     Эта ЭДС уравновешивается напряжением, подключенным к катушке: u = e_L = 0.

     (6.10)

     Таким образом, ток в индуктивности отстает по фазе от напряжения на 90^o из-за явления самоиндукции.      Уравнение вида (6.10) для реальной катушки, имеющей активное сопротивление R, имеет следующий вид:

     (6.11)

     Анализ выражения (6.11) показывает, что ЭДС самоиндукции оказывает препятствие (сопротивление) протеканию переменного тока, из-за чего ток в реальной индуктивной катушке отстает по фазе от напряжения на некоторый угол φ (0^o< φ < 90^o), величина которого зависит от соотношения R и L.      Выражение (6.11) в комплексной форме записи имеет вид:

     (6.12)

      где Z_L - полное комплексное сопротивление индуктивной катушки ;             Z_L - модуль комплексного сопротивления;            - начальная фаза комплексного сопротивления;- индуктивное сопротивление (фиктивная величина, характеризующая реакцию электрической цепи на переменное магнитное поле).       Полное сопротивление индуктивной катушки или модуль комплексного сопротивления

.

       Комплексному уравнению (6.12) соответствует векторная диаграмма (рис.6.5).

Рис. 6.5

       Из анализа диаграммы видно, что вектор напряжения на индуктивности опережает вектор тока на 90^o.     В цепи  переменного тока напряжения на  участках цепи складываются не арифметически, а геометрически.        Если мы поделим стороны треугольника напряжений на величину тока I_m, то перейдем к подобному треугольнику сопротивлений (рис. 6.6).

     Из треугольника сопротивлений получим несколько формул:                      ;;     Рис. 6.6

;

;           .

6.6. Емкость в цепи синусоидального тока

     Если к конденсатору емкостью C подключить синусоидальное напряжение, то в цепи протекает синусоидальный ток

;

.    (6.13)

      Из анализа выражений 6.13 следует, что ток опережает напряжение по фазе на 90^o.

      Выражение (6.13) в комплексной форме записи имеет вид:

,    (6.14)

       где - емкостное сопротивление, фиктивная расчетная величина, имеющая размерность сопротивления.

        Если комплексное сопротивление индуктивности положительно        , то комплексное сопротивление емкости отрицательно.

       На рис. 6.7 изображена векторная диаграмма цепи с емкостью.        Вектор тока опережает вектор напряжения на 90^o.

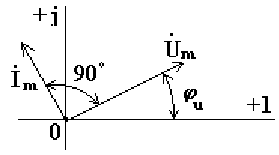Рис. 6.7