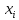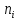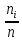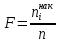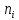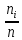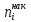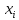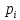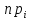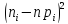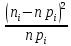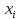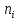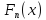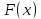- •Часть I. Проверка статистических гипотез
- •7. Имеются две выборки объемов и Показателя качества однотипной продукции, изготовленной двумя фирмами:
- •1) Критерий Колмогорова-Смирнова
- •2) Критерий однородности
- •3) Критерий Вилкоксона-Манна-Уитни
- •Часть II
- •Вариант 12
- •2) Задача максимизации
- •3) Проверка ответа графически:
- •3. Составить двойственную задачу к данной, решить одну их них симплекс - методом и найти решение другой
Федеральное государственное бюджетное образовательное учреждение высшего профессионального образования "Чувашский государственный университет им И.Н. Ульянова"
Математический анализ.
Типовой расчет.
Выполнил: ст. гр. МЭЭ-03-12
Чернышев И.В.
Проверила: Картузова Т.В.
Чебоксары 2013
Часть I. Проверка статистических гипотез
Дано
распределение признака X
(случайной величины X),
полученной по наблюдениям. Необходимо:
построить полигон (гистограмму), кумуляту
и эмпирическую функцию распределения,
найти среднюю арифметическую
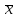 ;
медиану
;
медиану
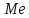 и моду
и моду
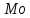 ;
дисперсию
;
дисперсию
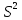 ,
среднее квадратическое отклонение
,
среднее квадратическое отклонение
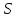 и коэффициент вариации
и коэффициент вариации
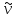 ;
начальные
;
начальные
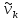 и центральные
и центральные
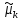 моменты
моменты
 - го порядка (
- го порядка ( );
коэффициент асимметрии
);
коэффициент асимметрии
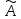 и эксцесс
и эксцесс
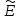
1.
X
- число сделок на фондовой бирже за
квартал;
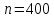
|
|
0 |
1 |
2 |
3 |
4 |
5 |
6 |
7 |
8 |
9 |
10 |
|
|
146 |
97 |
73 |
34 |
23 |
10 |
6 |
3 |
4 |
2 |
2 |
|
|
0,365 |
0,2425 |
0,1825 |
0,085 |
0,0575 |
0,025 |
0,015 |
0,0075 |
0,01 |
0,005 |
0,005 |
|
|
146 |
243 |
316 |
350 |
373 |
383 |
389 |
392 |
396 |
398 |
400 |
|
|
0,365 |
0,6075 |
0,79 |
0,875 |
0,9325 |
0,9575 |
0,9725 |
0,98 |
0,99 |
0,995 |
1 |
Полигон (гистограмма) распределения частот:
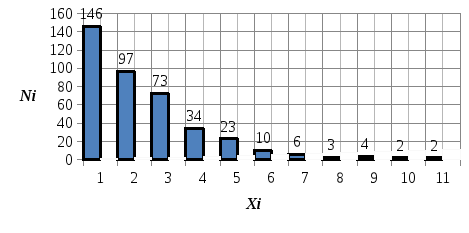
Кумулята
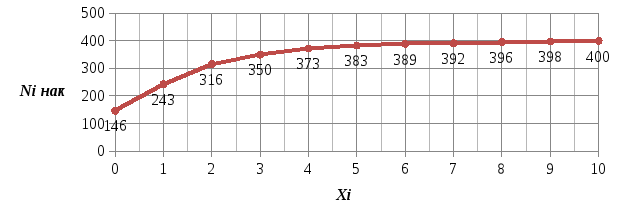
Эмпирическая функция распределения:
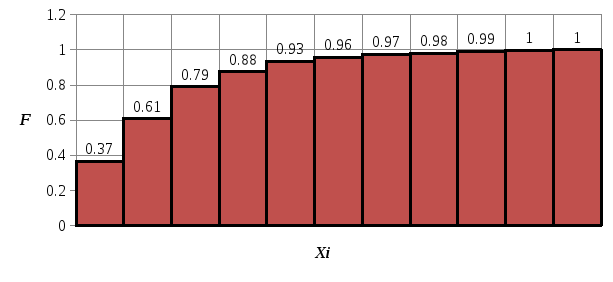
Среднее арифметическое:
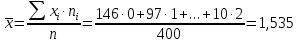
Медиана (значение признака, которое приходится на середину ранжированного ряда)
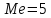
Мода (варианта, которой соответствует наибольшая частота)
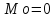
Дисперсия
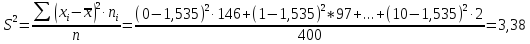
Среднее квадратическое отклонение
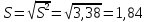
Коэффициент вариации

Начальные
моменты
 - го порядка (
- го порядка (
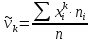

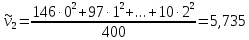
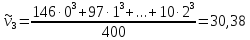
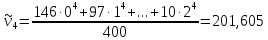
Центральные
моменты
 - го порядка (
- го порядка (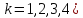
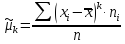
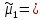


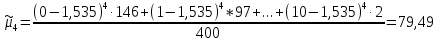
Коэффициент асимметрии
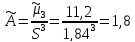
Эксцесс
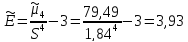
2. X
- удой коров на молочной ферме за
лактационный период (в ц.);
 (коров)
(коров)
|
|
4-6 |
6-8 |
8-10 |
10-12 |
12-14 |
14-16 |
16-18 |
18-20 |
20-22 |
22-24 |
24-26 |
|
|
1 |
3 |
6 |
11 |
15 |
20 |
14 |
12 |
10 |
6 |
2 |
|
|
0,01 |
0,03 |
0,06 |
0,11 |
0,15 |
0,2 |
0,14 |
0,12 |
0,1 |
0,06 |
0,02 |
|
|
1 |
4 |
10 |
21 |
36 |
56 |
70 |
82 |
92 |
98 |
100 |
|
|
0,01 |
0,04 |
0,1 |
0,21 |
0,36 |
0,56 |
0,7 |
0,82 |
0,92 |
0,98 |
1 |
Полигон (гистограмма) распределения частот:

Кумулята:
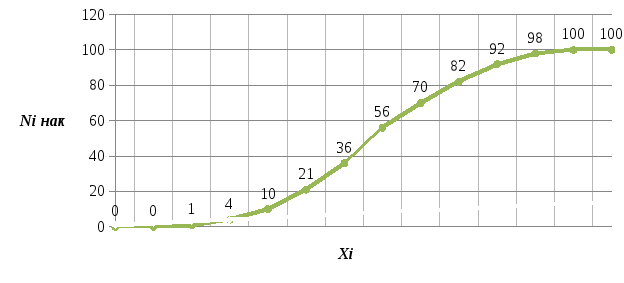
Эмпирическая функция распределения:
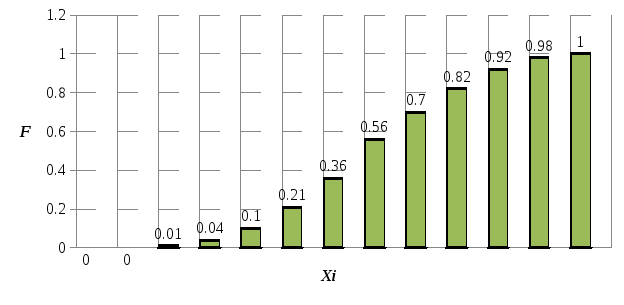
Среднее арифметическое:
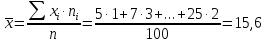
Медиану определим по кумуляте:
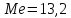
Моду определим по гистограмме:
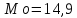
Дисперсия

Среднее квадратическое отклонение
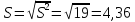
Коэффициент вариации
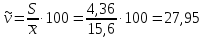
Начальные
моменты
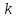 - го порядка (
- го порядка (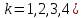
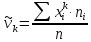
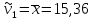

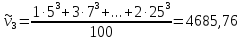
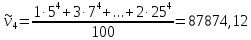
Центральные
моменты
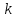 - го порядка (
- го порядка (
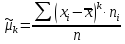

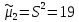
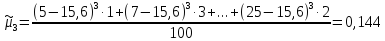
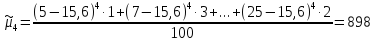
Коэффициент асимметрии
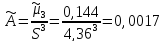
Эксцесс
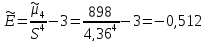
3.
По выборкам объемом
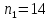 и
и
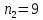 найдены средние размеры деталей
соответственно
найдены средние размеры деталей
соответственно
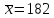 и
и
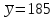 мм. Установлено, что размер детали,
изготовленный каждым автоматом, имеет
нормальный закон распределения. Известны
дисперсии
мм. Установлено, что размер детали,
изготовленный каждым автоматом, имеет
нормальный закон распределения. Известны
дисперсии
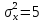 и
и
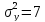 для первого и второго автоматов. На
уровне значимости
для первого и второго автоматов. На
уровне значимости
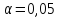 выявить влияние на средний размер детали
автомата, на котором она изготовлена.
Рассмотреть два случая: 1)
выявить влияние на средний размер детали
автомата, на котором она изготовлена.
Рассмотреть два случая: 1)
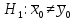 ;
2)
;
2)
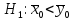
Нулевая
гипотеза
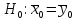 (т.е. автомат не оказывает влияния на
размер).
(т.е. автомат не оказывает влияния на
размер).
Рассчитаем статистику:
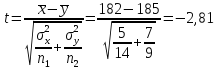
1)
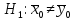 (т.е. средний размер детали зависит от
выбора автомата) - двусторонняя критическая
область
(т.е. средний размер детали зависит от
выбора автомата) - двусторонняя критическая
область
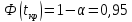
По
таблице значений функции Лапласа:
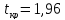
Получили:
 .
.
Нулевая гипотеза отвергается. Т.е. средний размер детали зависит от выбора автомата.
2)
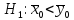 (т.е. влияние второго автомата больше)
- односторонняя критическая область
(т.е. влияние второго автомата больше)
- односторонняя критическая область
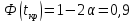
По
таблице значений функции Лапласа:

Получили:
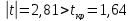 .
.
Нулевая гипотеза отвергается. Т.е. влияние второго автомата больше.
4.
Имеются следующие данные о качестве
детского питания, изготовленного
различными фирмами (в баллах): 40, 39, 42
,37, 38, 43, 45, 41, 48. Есть основание полагать,
что показатель качества продукции
последней фирмы зарегистрирован неверно
(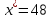 ).
Является ли это значение аномальным
(резко выделяющимся) на 5% уровне значимости
(
).
Является ли это значение аномальным
(резко выделяющимся) на 5% уровне значимости
(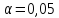 )
)
Нулевая
гипотеза
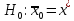 (т.е значение
(т.е значение
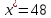 принадлежит к остальным наблюдениям).
принадлежит к остальным наблюдениям).
Исключим
значение
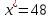 и для остальных найдем среднее
арифметическое и среднее квадратическое
отклонение (
и для остальных найдем среднее
арифметическое и среднее квадратическое
отклонение (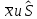 ):
):
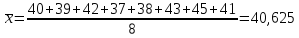
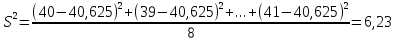
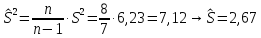
Рассчитаем значение статистики, имеющий распределение Стьюдента
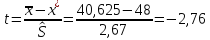
По таблице значений критерия Стьюдента:
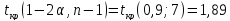
Получили:
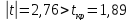 .
.
Нулевая
гипотеза отвергается, т.е. значение
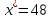 является аномальным и его следует
отбросить.
является аномальным и его следует
отбросить.
5.
Вступительный экзамен проводился на
двух факультетах института. На
экономическом факультет из
 абитуриентов выдержали экзамен
абитуриентов выдержали экзамен
 человек, а на финансово-кредитном из
человек, а на финансово-кредитном из
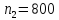 абитуриентов -
абитуриентов -
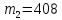 .
На уровне значимости
.
На уровне значимости
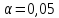 проверить гипотезу об отсутствии
существенных различий в уровне подготовки
абитуриентов двух факультетов. Рассмотреть
два случая: 1)
проверить гипотезу об отсутствии
существенных различий в уровне подготовки
абитуриентов двух факультетов. Рассмотреть
два случая: 1)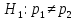 ;
2)
;
2)
Нулевая
гипотеза:
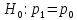 (т.е. уровни подготовки абитуриентов
одинаковы)
(т.е. уровни подготовки абитуриентов
одинаковы)
Найдем
выборочные доли
 и
и
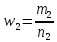 :
:
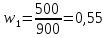 ;
;
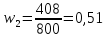
Рассчитаем выборочную долю признака:
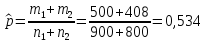
Рассчитаем значение статистики:
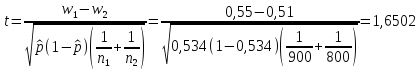
1)
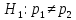 (уровни подготовки абитуриентов
отличаются) - одностороння критическая
область:
(уровни подготовки абитуриентов
отличаются) - одностороння критическая
область:

По
таблице значений функции Лапласа:
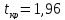
Получили:
 .
.
Нулевая гипотеза принимается, т.е. полученные данные не противоречат гипотезе об одинаковом уровне подготовки абитуриентов.
2)
 (уровень подготовки абитуриентов
экономического факультета лучше уровня
подготовки студентов финансово -
кредитного) - одностороння критическая
область:
(уровень подготовки абитуриентов
экономического факультета лучше уровня
подготовки студентов финансово -
кредитного) - одностороння критическая
область:
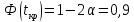
По
таблице значений функции Лапласа:
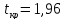
Получили:
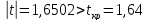
Нулевая гипотеза отвергается, т.е. полученные данные противоречат гипотезе о лучшем уровне подготовки абитуриентов экономического факультета.
6.
На уровне значимости
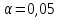 проверить гипотезу о нормальном законе
распределения признака (случайной
величины)
проверить гипотезу о нормальном законе
распределения признака (случайной
величины)
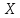 ,
используя критерий согласия: 1)
,
используя критерий согласия: 1)
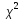 - Пирсона; 2) Колмогорова
- Пирсона; 2) Колмогорова
|
|
4-6 |
6-8 |
8-10 |
10-12 |
12-14 |
14-16 |
16-18 |
18-20 |
20-22 |
22-24 |
24-26 |
|||||||
|
|
1 |
3 |
6 |
11 |
15 |
20 |
14 |
12 |
10 |
6 |
2 |
|||||||
|
|
0,01 |
0,027 |
0,058 |
0,105 |
0,153 |
0,18 |
0,173 |
0,135 |
0,086 |
0,044 |
0,019 |
|||||||
|
|
1 |
2,7 |
5,8 |
10,5 |
15,3 |
18 |
17,3 |
13,5 |
8,6 |
4,4 |
1,9 |
|||||||
|
|
0,25 |
0,25 |
0,09 |
4 |
10,89 |
2,25 |
1,96 |
2,89 |
||||||||||
|
|
0,0263 |
0,0238 |
0,0059 |
0,22 |
0,63 |
0,167 |
0,228 |
0,459 |
||||||||||
Нулевая
гипотеза
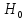 - случайная величина
- случайная величина
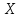 распределена нормально
распределена нормально
1)
Критерий Пирсона (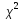 )
)
Вероятности
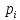 рассчитываются по формуле
рассчитываются по формуле
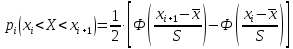
По
данным примера 2 имеем
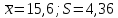
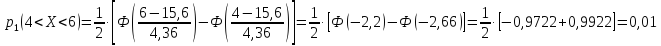
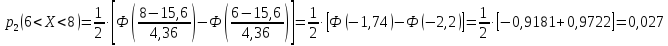
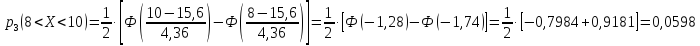

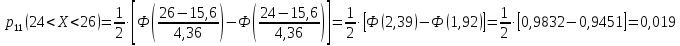
Определим меру расхождения эмпирических и теоретических частот:

Число степеней свободы:
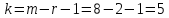
где
 - число интервалов эмпирического
распределения
- число интервалов эмпирического
распределения
 - число параметров теор. распределения
- число параметров теор. распределения
По
таблице находим:
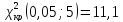
Получили:
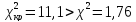
Т.е. гипотеза о выбранном теоретическом нормальном законе распределения согласуется с опытными данными.
2) Критерий Колмогорова
|
|
4 |
6 |
8 |
10 |
12 |
14 |
16 |
18 |
20 |
22 |
24 |
26 |
|
|
1 |
3 |
6 |
11 |
15 |
20 |
14 |
12 |
10 |
6 |
|
2 |
|
|
0,01 |
0,01 |
0,04 |
0,1 |
0,21 |
0,36 |
0,56 |
0,7 |
0,82 |
0,92 |
0,98 |
1 |
|
|
0,0039 |
0,0139 |
0,0409 |
0,0986 |
0,2032 |
0,3567 |
0,5359 |
0,7088 |
0,8436 |
0,9282 |
0,9732 |
0,9916 |
|
|
0,0061 |
0,0039 |
0,0009 |
0,0014 |
0,0068 |
0,0043 |
0,0241 |
0,0088 |
0,0238 |
0,0092 |
0,0064 |
0,0084 |
Значения
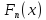 это накопленные частости
это накопленные частости

Первый
конец рассчитываем для

Для
построения
 в случае нормального закона воспользуемся
формулой:
в случае нормального закона воспользуемся
формулой:
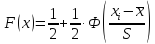
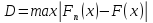
Получим:
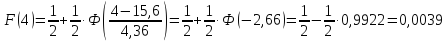
.................................................................................................................................................
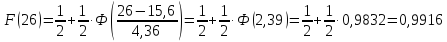
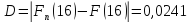
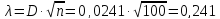
При и
и
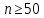 :
:
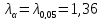
Получили:
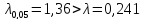
Т.е. гипотеза о выбранном теоретическом нормальном законе распределения согласуется с опытными данными.