Признак Коши (радикальный признак)

Теорема. Если для ряда с неотрицательными членами существует предел

,

( )

то ряд сходится при и расходится при.

Доказательство. Из условия ( . ) следует, что для произвольного справедливы неравенства

, или .

Пусть , тогда выбираятаким образом, чтобы величина. В этом случае все члены ряда меньше соответствующих степеней бесконечной сходящейся геометрической прогрессии, т.е. в силу теоремы о сравнении ряд сходится.

Пусть теперь , тогда выберемтаким, чтобы. В этом случае необходимое условие сходимости ряда не выполняется, т.е. ряд расходится. Теорема доказана.

Пример . . Исследовать сходимость ряда .

Решение. Применим признак Коши:

.

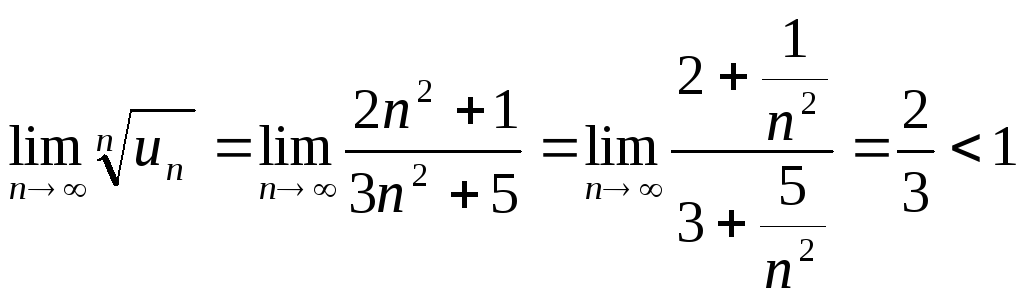Следовательно, ряд сходится.

Пример . . Определить сходимость ряда .

Решение.

,

т.е. признак Коши не дает ответа на вопрос о сходимости ряда. Проверим выполнение необходимых условий сходимости.

,

таким образом, необходимое условие сходимости не выполняется, значит, ряд расходится.

Интегральный признак Коши

Теорема. Если ‑‑ непрерывная невозрастающая функция, определенная при, то числовой ряди интегралсходятся или расходятся одновременно.

Доказательство. В силу того, что монотонна, то длявыполняется неравенство, или, проинтегрировав последнее неравенство на отрезке, получаем

.

( 32 )

Рассмотрим ряд

.

( 33 )

Его ‑я частичная сумма имеет вид

.

( 34 )

Сходимость ряда (33) означает существование конечного предела последовательности частичных сумм (34), т.е. сходимость несобственного интеграла , потому что.

Если ряд сходится, то по теореме о сравнении рядов в силу левого неравенства (32) должен сходится и ряд (33), а следовательно и несобственный интеграл . И наоборот, если сходится интеграл, т.е. ряд(33), то по теореме сравнения должен сходиться ряд, следовательно и данный ряд должен сходится.

Пример . . Ряд сходится прии расходится ‑‑, т.к. соответствующий несобственный интегралсходится прии расходится для.

Ряд называетсяобобщенным гармоническим рядом.

Знакопеременные ряды. Знакочередующиеся ряды

Определение. Числовой ряд называется знакопеременным, если он имеет бесконечное число как положительных, так и отрицательных членов.

Определение. Числовой ряд называется знакочередующимся, если для любого члены рядаиимеют разные знаки.

Знакочередующийся ряд можно записать в виде:

, где .

( 35 )

Признак Лейбница

Теорема. Если члены знакочередующегося ряда убывают по абсолютной величине и предел его общего члена приравен нулю, т.е., то ряд сходится, а его сумма не превосходит первого члена:.

Доказательство. Запишем частичную сумму четного числа членов . В силу первого условия теоремы каждая разность в скобках является положительным числом, и поэтому последовательность частичных суммявляется возрастающей.

С другой стороны, можно представить следующим образом:, отсюда следует, что.

Отсюда, последовательность возрастает и ограничена, значит она имеет предел. При этом из неравенстваследует, что. А так каки, по второму условию теоремы, то.

Любая последовательность частичных сумм ряда сходится к пределу, а это и означает сходимость данного ряда.

Следствие. Погрешность при приближенном вычислении суммы сходящегося знакочередующегося ряда, удовлетворяющего условиям теоремы Лейбница, по абсолютной величине не превышает абсолютной величины первого отброшенного члена.

Пример . . .

Данный ряд сходится по признаку Лейбница, потому что его члены убывают по абсолютной величине и при.