1.5. Использования метода градиентного спуска

Рассмотрим функцию . Вычислим ее частные производные, и образуем с их помощью вектор, который называют градиентом функции:

Здесь - единичные вектора, параллельные координатным осям. Частные производные характеризуют изменение функциипо каждой независимой переменной в отдельности. Это помогает определить поведение функции в окрестности точки. Направление этого вектора является направлением быстрого возрастания в данной точки.

Основная идея состоит в том, чтобы двигаться к минимуму в направлении наиболее быстрого убывания функции, которое определяется антиградиентом. Выбираем начальную точку, вычисляем в ней градиент функции и делаем небольшой шаг. В результате мы придем в точку, в которой значение функции будет меньше первоначального. В новой точке повторим процедуру. Продолжая выполнения этой процедуры, найдет значение параметров функции ив точке минимума.

Метод градиентного спуска требует вычисления градиента целевой функции на каждом шаге. Частные производные в нужных точках вычисляются приближенно, заменяя их соответствующими разностными отношениями:

В этом случае задается постоянный шаг, и точность вычислений зависит от шага. Но не целесообразно из-за этого брать маленький шаг, так как основное время уходит на вычисление градиента функции. Целесообразней сделать метод градиентного спуска с изменяющимся шагом, который уменьшит время вычислений в несколько раз.

В нашем случае вместо функции применяется функция(). Графически это выглядит так:

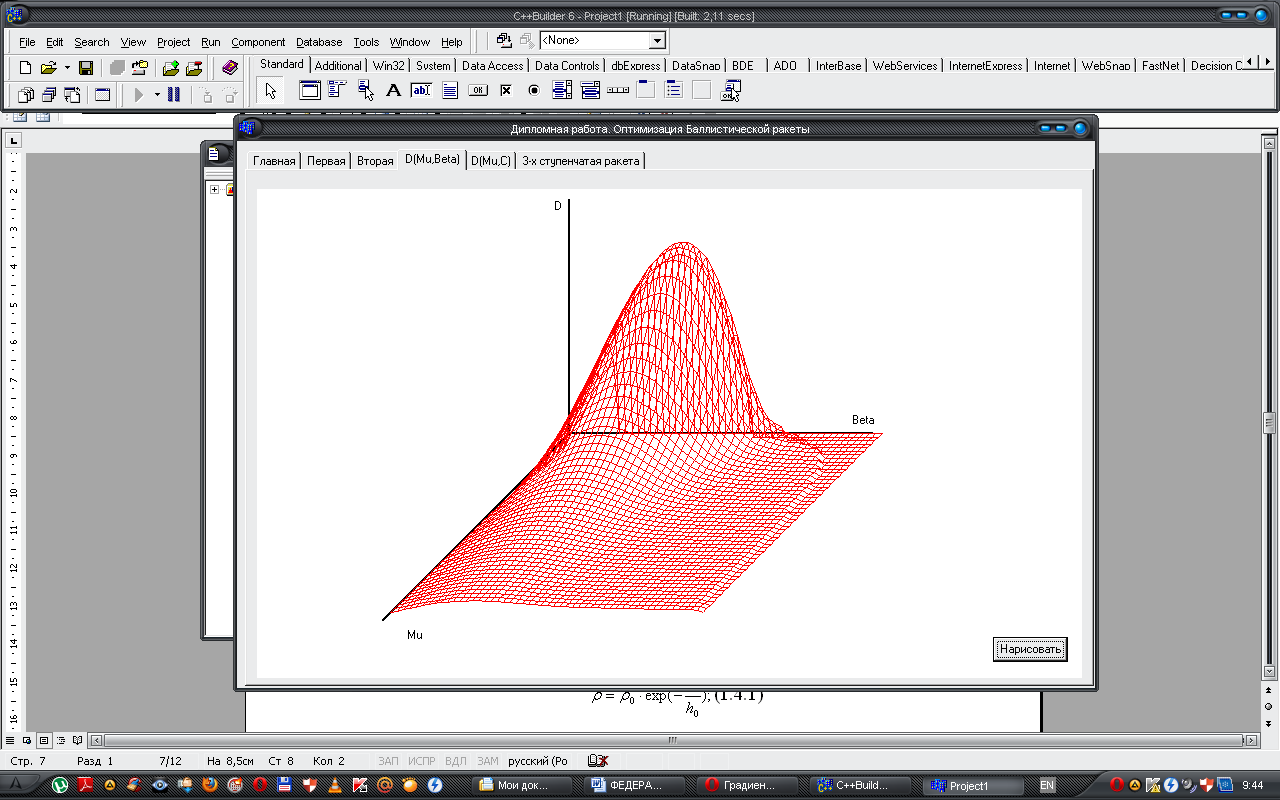
Или можно представить в виде слоев:

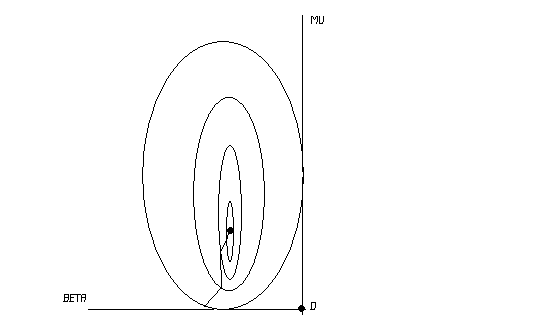
На рисунке показана траектория поиска наименьшего значения функции.

Этот метод будем использовать для поиска оптимальных параметров мгновенной скорости сгорания топлива Mu и угла атаки (или константы С от которой зависит как).

1.6. Оптимизация изменения плотности воздуха от высоты

Из курса общей физики мы знаем, что плотность воздуха определяется формулой:

(1.4.1)

где – высота над уровнем моря (), – высота МБР над уровнем Земли,– плотность воздуха на уровне Земли.

Но исследуя экспериментальные данные зависимости плотности воздуха от высоты, указанные в книге А.В. Солодова «Инженерный справочник по космической технике» (см. Приложение 1).

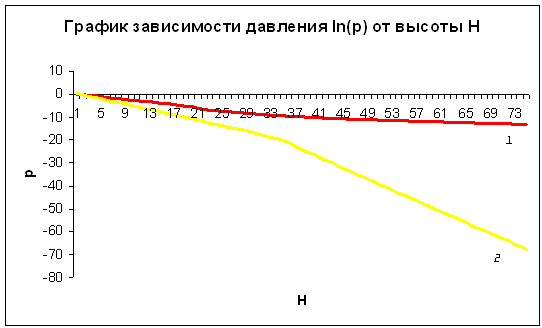
1 – по формуле 1.4.1 и 2 – экспериментально.

Видно не точность формулы (1.4.1). Для решения этой проблемы будем применять численные методы для более точного результата.

Используем метод, рассмотренный выше (метод линейной интерполяции пункт 1.4) в промежутке , а в промежутке используем метод параболической аппроксимации. Такая аппроксимация является не линейным, многочленом второй степени.

Коэффициенты определяются по методу наименьших квадратов. Запишем квадратичное отклонение.

Приравняем к нулю частные производные:

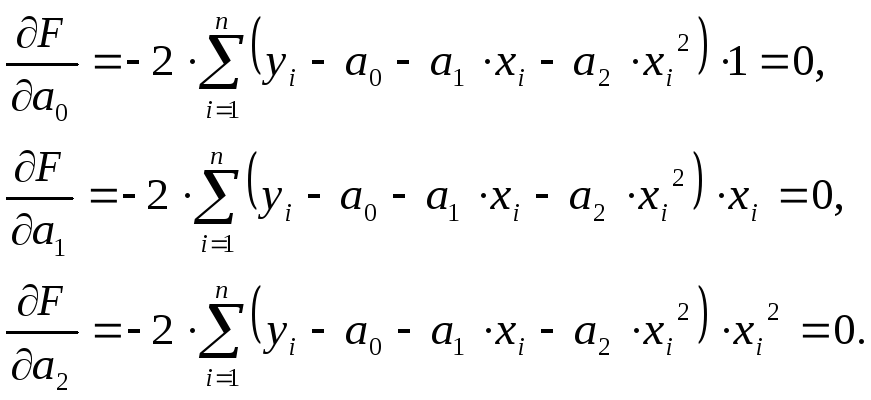
Выполнив преобразования, получим систему уравнений с тремя неизвестными (a₀,a₁,a₂).

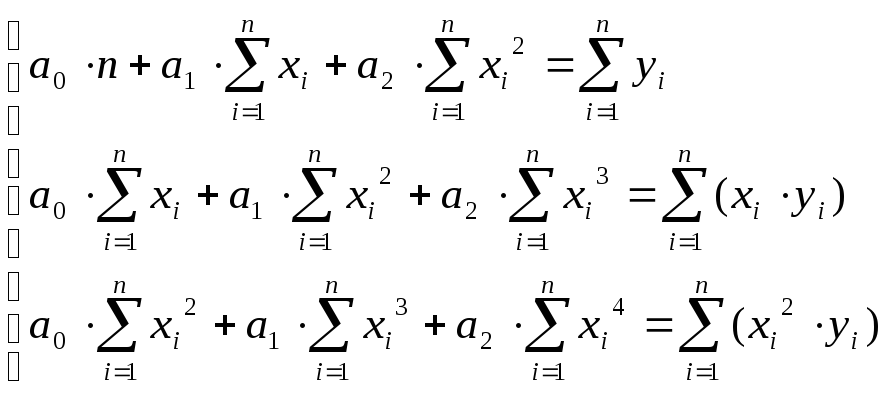
Введем обозначения:

Определим неизвестные коэффициенты a₀,a₁,a₂

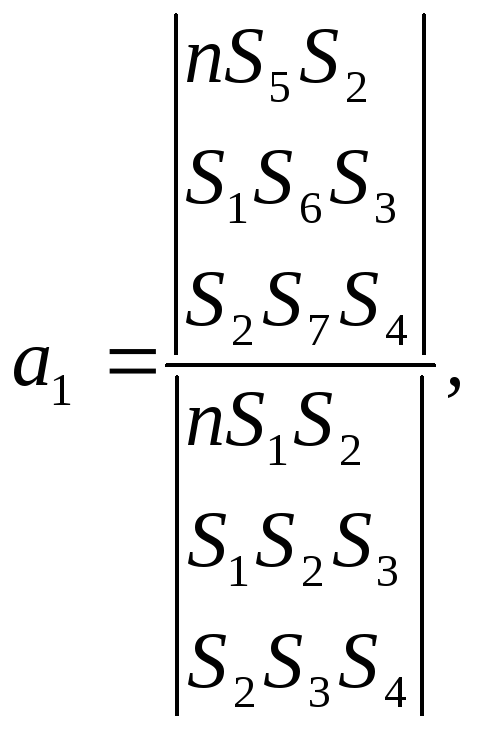
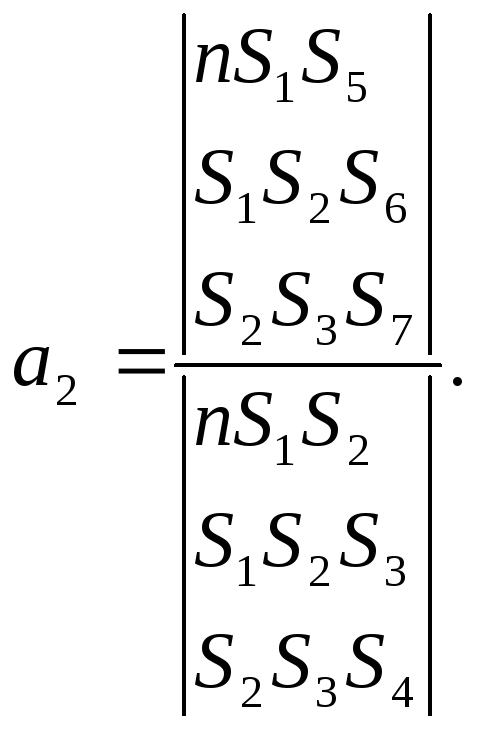
Необходимое условие: определитель системы

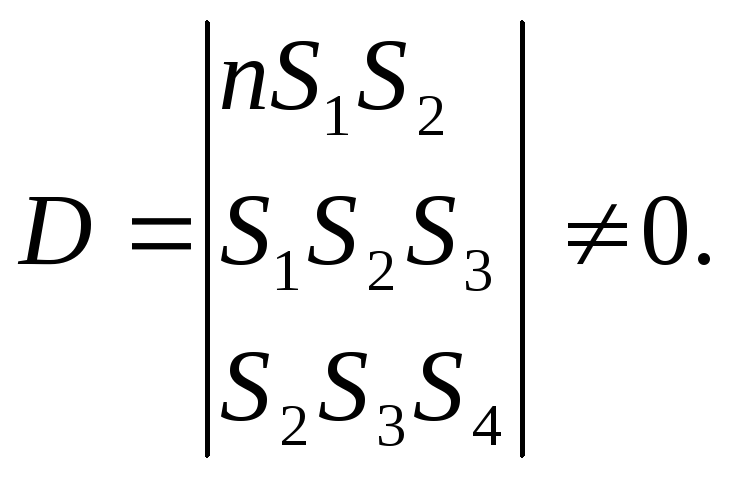
В результате мы можем с большей точности узнать плотность воздуха на любой высоте.