
- •Содержание
- •Глава 1. Решение задачи ……………………………………………………….. 7
- •Глава 2. Результаты …………………………………………………………… 18
- •Введение
- •Литературный обзор
- •Глава 1. Решение задачи
- •1.1. Постановка задачи
- •1.2. Вывод уравнения движения
- •1.3. Методика численного решения дифференциального уравнения
- •1.4. Использования метода линейной аппроксимации
- •1.5. Использования метода градиентного спуска
- •1.6. Оптимизация изменения плотности воздуха от высоты
- •1.7. Моделирование полета
- •Глава 2. Результаты
- •2.1. Параметрические кривые одноступенчатой мбр
- •2.2. Исследование дальности полета межконтинентальной баллистической ракеты
- •График зависимости дальности полета при оптимальных параметрах скорости сгорания топлива Mu и константы c
- •Заключение
- •Список использованной литературы
- •Приложение
Глава 1. Решение задачи
1.1. Постановка задачи
Рассмотрим межконтинентальную баллистическую ракету Р-9 / Р-9А (8К75)SS-8/(Sasin), которая базируется на экваторе и стартует в направление вращения Земли.
Исследовать полет одноступенчатой ракеты, если угол атаки
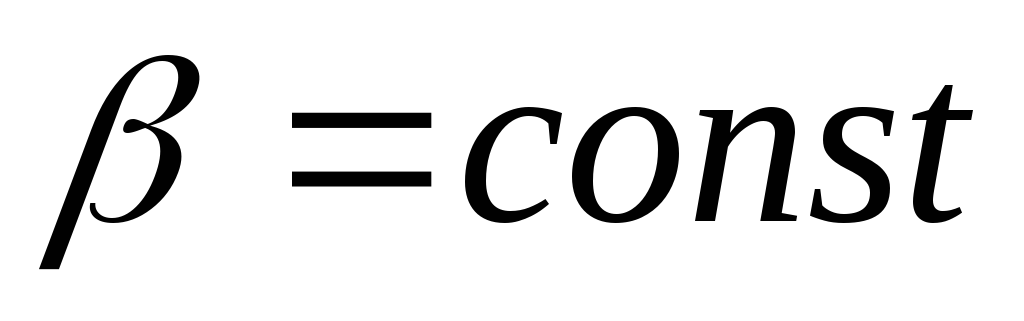 и масса боеголовки
и масса боеголовки
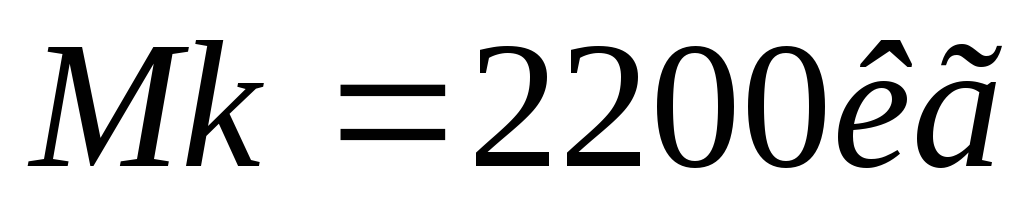 .
Определить оптимальные параметры угла
атаки
.
Определить оптимальные параметры угла
атаки и мгновенной скорости сгорания топлива
и мгновенной скорости сгорания топлива
 ,
при которых дальность полета будет
максимальной
,
при которых дальность полета будет
максимальной
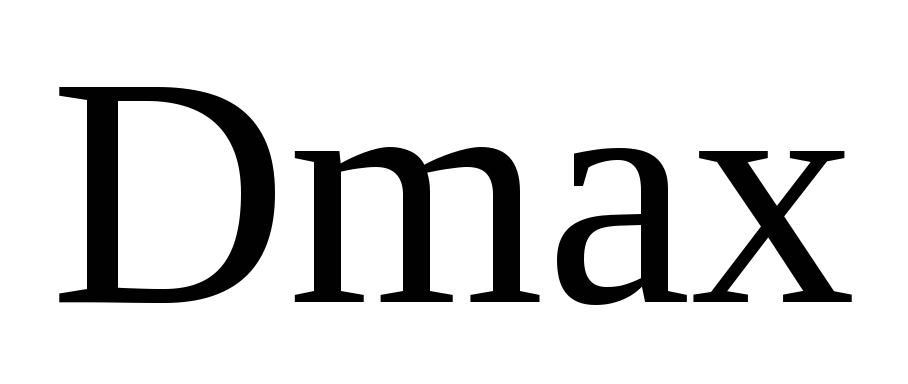 .
.Исследовать полет одноступенчатой ракеты, если угол атаки
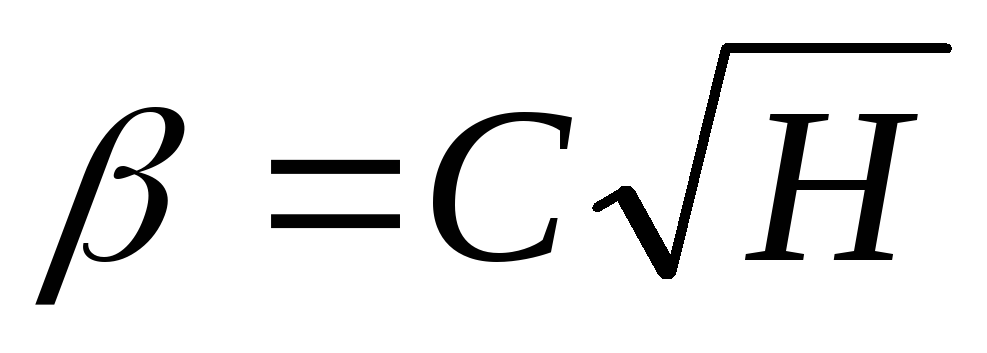 и масса боеголовки
и масса боеголовки
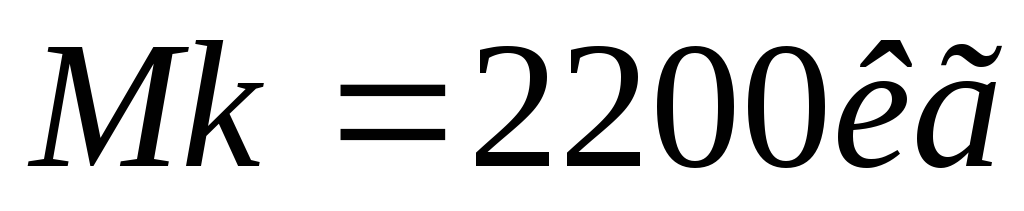 .
Определить оптимальные параметры
константы
.
Определить оптимальные параметры
константы
 и мгновенной скорости сгорания топлива
и мгновенной скорости сгорания топлива
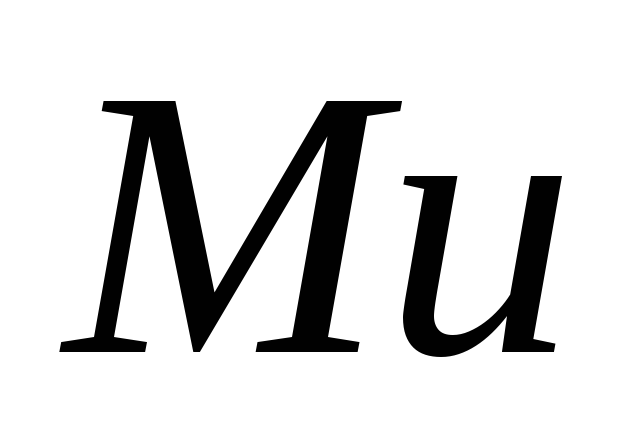 ,
при которых дальность полета будет
максимальной
,
при которых дальность полета будет
максимальной
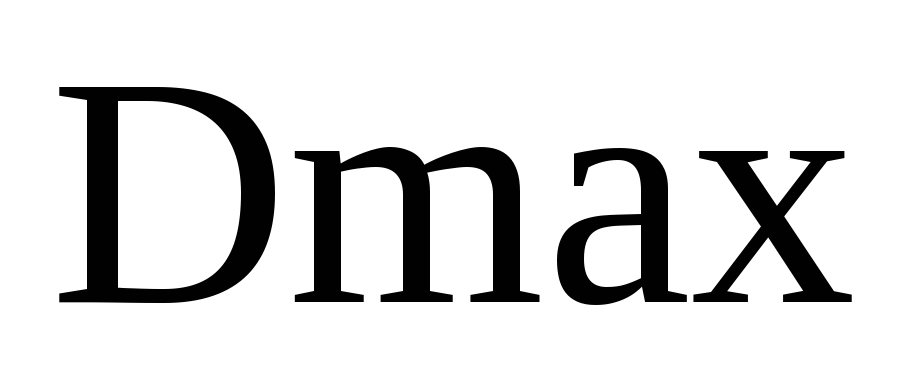 .
.Исследовать полет двухступенчатой ракеты.
Исследовать полет трехступенчатой ракеты.
Определить максимальную массу боеголовки
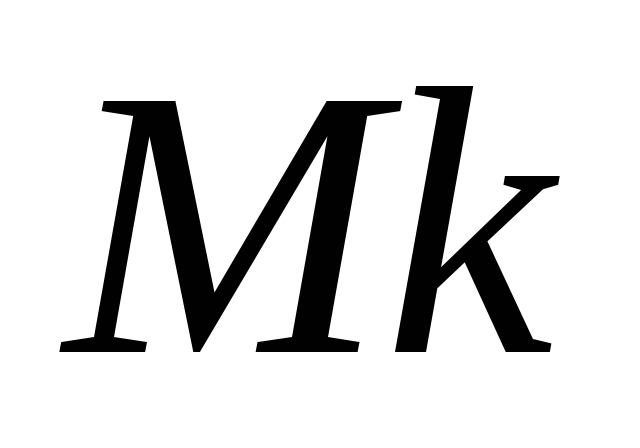 на некотором расстоянии.
на некотором расстоянии.
1.2. Вывод уравнения движения
Движение Земли и МБР является примером задачи двух тел. Решать эту задачу будем в не инерциальной системе отсчета.
Уравнение движения МБР будет являться уравнение Мещерского:
![]()
где
![]() –
сила инерции,
–
сила инерции,![]() –
реактивная сила,
–
реактивная сила,![]() – сила сопротивления воздуха,
– сила сопротивления воздуха,![]() –
сила Кориолиса,
–
сила Кориолиса,![]() – масса МБР,
– масса МБР,![]() – ускорение свободного падения,
– ускорение свободного падения,![]() –
ускорение МБР.
–
ускорение МБР.
![]()
где
![]() –
угловая скорость вращения Земли.
–
угловая скорость вращения Земли.
![]()
где
![]() – скорость сгорания топлива,
– скорость сгорания топлива,![]() – относительная скорость отделяющихся
частиц.
– относительная скорость отделяющихся
частиц.
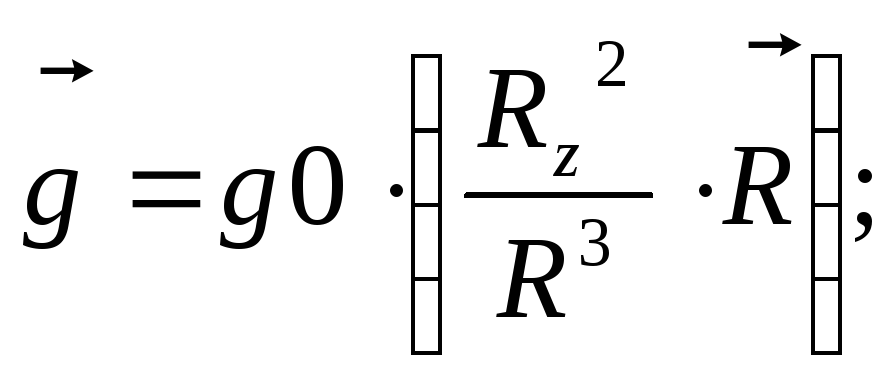
![]()
где
![]() – ускорение свободного падения на
экваторе,
– ускорение свободного падения на
экваторе,![]() – радиус Земли,
– радиус Земли,![]() – расстояние от центра Земли до МБР,
– расстояние от центра Земли до МБР,![]() – масса Земли,
– масса Земли,![]() – постоянная тяготения.
– постоянная тяготения.
![]()
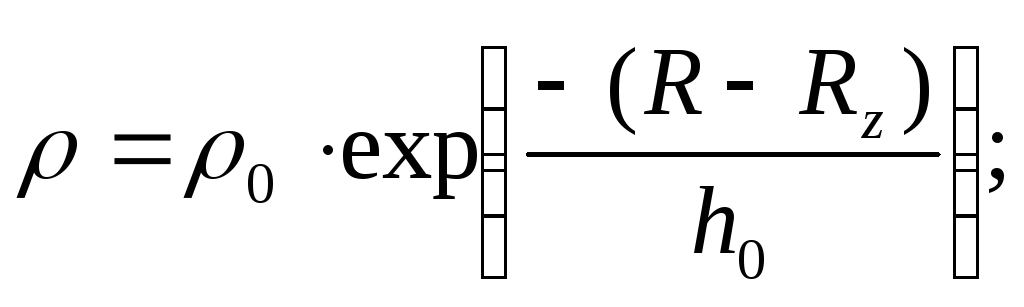
где
![]() – плотность воздуха,
– плотность воздуха,![]() – диаметр МБР,
– диаметр МБР,![]() – скорость МБР, γ – угол раствора МБР,
– скорость МБР, γ – угол раствора МБР,![]() –
на поверхности Земли,
–
на поверхности Земли,![]() –
высота над уровнем моря.
–
высота над уровнем моря.
![]()
В результате получаем
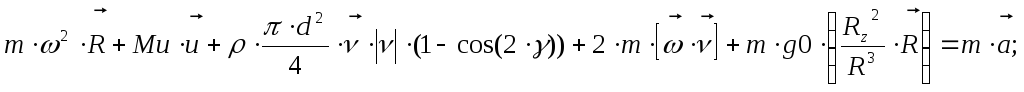
![]()
Для целей численного моделирования удобно записать уравнение в декартовых координатах.
Координаты x:
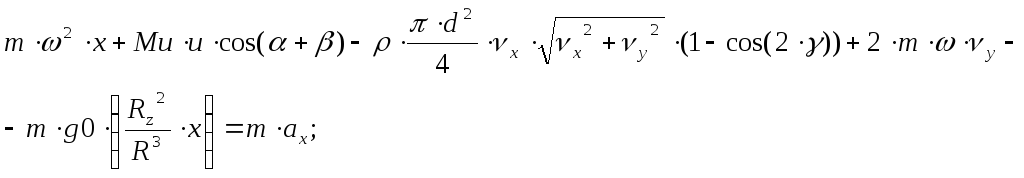
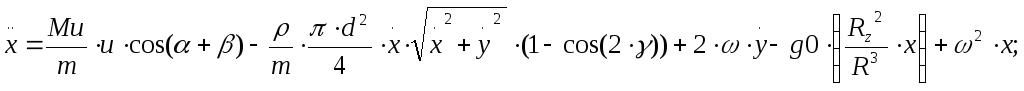
Координаты y:
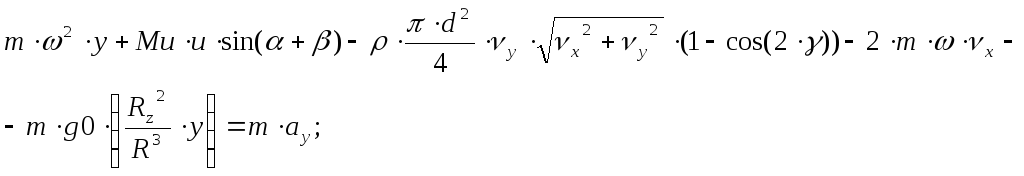
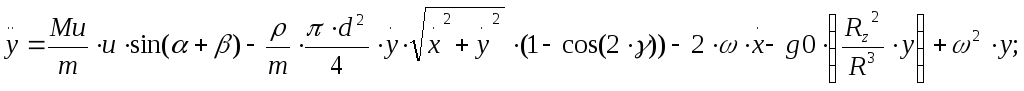
где
![]()
Для упрощения формулы введем коэффициенты:
![]()

Получим систему:
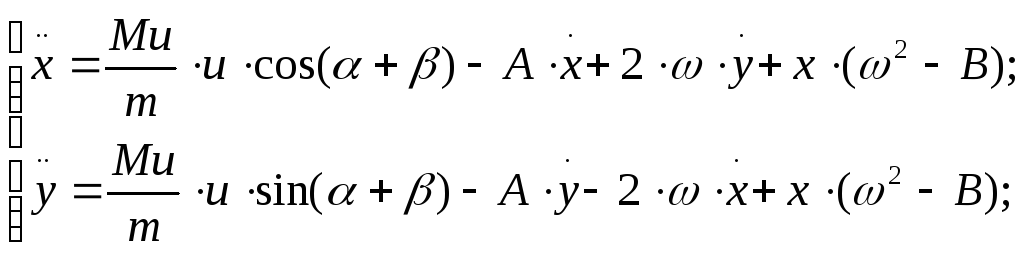
С истема
является задачей Коши для обыкновенных
дифференциальных уравнений. Для решения
задачи Коши нужно задать начальные
условия:
истема
является задачей Коши для обыкновенных
дифференциальных уравнений. Для решения
задачи Коши нужно задать начальные
условия:
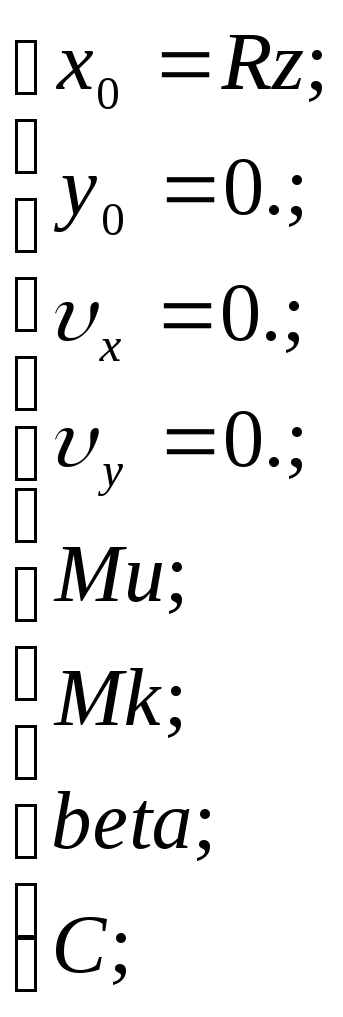
1.3. Методика численного решения дифференциального уравнения
Меерсон
предложил модификацию метода Рунге-Кутты
четвертого порядка, который заключается
в построение вычислительных схем в
тейлоровском разложении искомого
решения уравнения
![]() учитывая члены до четвертого включительно.
Меерсон ввел оценку погрешность на
каждом шаге, и принимать решение об
изменении шага. Схему Меерсона приведем
к виду, удобному для программирования,
учитывая члены до четвертого включительно.
Меерсон ввел оценку погрешность на
каждом шаге, и принимать решение об
изменении шага. Схему Меерсона приведем
к виду, удобному для программирования,
![]()
где
![]()
![]()
![]()
![]()
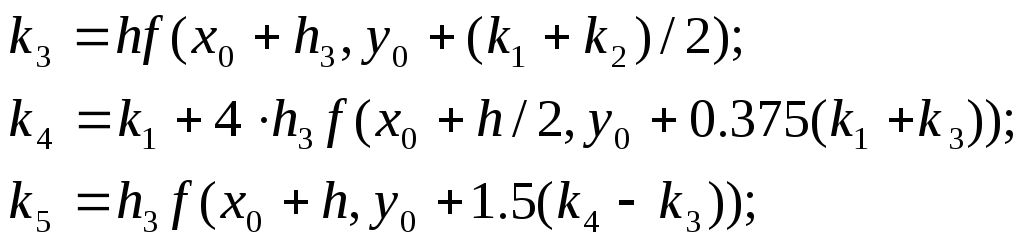
Схема
Меерсона требует на каждом шаге вычислять
правую часть ОДУ в пяти точках, но за
счет только одного дополнительного
коэффициента
![]() ,
по сравнению с классической схемой
Рунге-Кутты на каждом шаге можно
определить погрешность решения
,
по сравнению с классической схемой
Рунге-Кутты на каждом шаге можно
определить погрешность решения![]() по формуле
по формуле
![]()
Для
автоматического выбора шага интегрирования
рекомендуется следующий критерий. Если
абсолютное значение величины
![]() ,
окажется больше допустимой заданной
погрешности
,
окажется больше допустимой заданной
погрешности![]() ,
,
![]()
то шаг h уменьшится в два раза. При выполнении условия
![]()
шаг можно удвоить.
1.4. Использования метода линейной аппроксимации
В расчетах требуется установить функцию f(x) для всех значений x отрезка [a,b], если известны ее значения в некотором конечном числе точек этого отрезка. Одним из способов приближения функции является интерполяция.
Простейшим и часто используемым видом интерполяции является линейная интерполяция. Она состоит в том, что заданные точки xi, yi при i=0,1,2,..n соединяются прямолинейными отрезками и функцию f(x) можно приближенно представить ломанной с вершинами в данных точках.
Уравнения каждого отрезка в общем случае разные. Поскольку имеется n интервалов (xi-1,xi), то для каждого из них в качестве уравнения интерполяционного многочлена используется уравнения прямой, проходящей через две точки. В частности, для i-го интеграла можно написать уравнение прямой, проходящей через точки (xi-1,yi-1)и(xi,yi), в виде
![]()
Отсюда
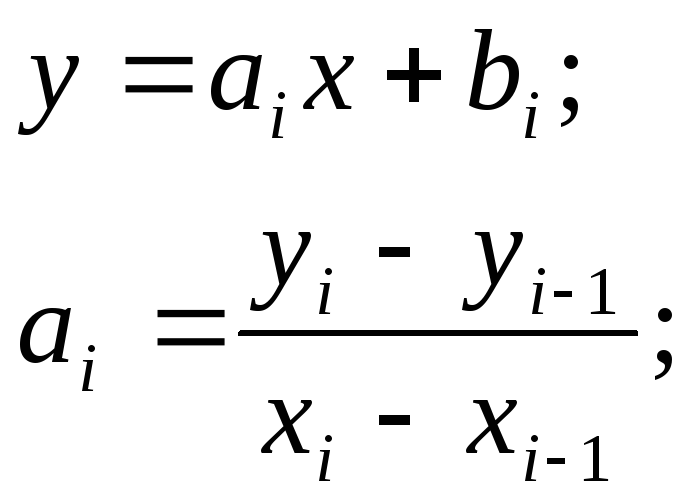
![]()
Следовательно, при использовании линейной интерполяции сначала нужно определить интервал, в котором попадает значение аргумента x, а затем подставить его в формулу и найти приближенное значение функции в этой точки.
