1. Знайти область визначення функції:

z=.

2. Визначити похідну складеної функції за аргументом t:

z=arcsin , x=sint, y=cost

3. Знайти рівняння дотичної площини й нормалі до поверхні σ у точці м0:

σ: x²+y² – xz+ yz-3x=11, M₀(1,4,-1).

4. Перевірити, чи є функція z = f(x, y) розв`язком даного диференціального рівняння

y - x =0, z= ln(x²+y²) .

5. Дослідити функцію z = f(x; y) на екстремум і знайти найбільше й найменше значення цієї функції в замкненій області :

z=x²y( 4-x-y) : x=0, y=0, y= 6-x.

6. Змінити порядок інтегрування:

.

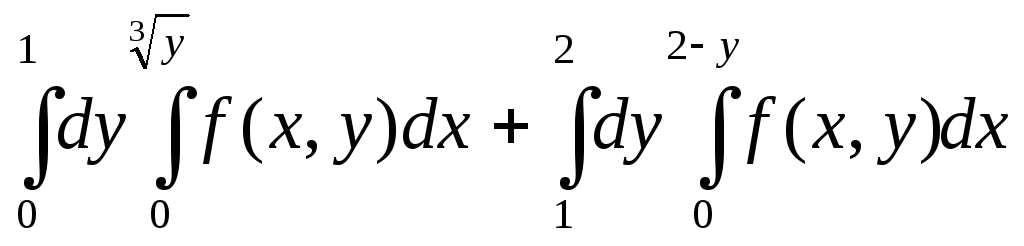7. Знайти площу фігури S за допомогою подвійного інтеграла:

a) S: y= , y= , x=16;

b) S: x²- 2x+y²=0, x²-6x+y²=0, y= ; y= x.

8. Знайти масу пластини D з поверхневою густиною ρ:

D: x=2, y≥0, y²=2x, ρ=.

9. Знайти об'єм тіла V:

z= , z=2, x²+y²≤27.

10. Знайти масу тіла V:

V: x²+y²= , x²+y²= z, x≥0, y≥0, .

11. Обчислити момент інерції однорідного тіла V щодо зазначеної осі:

V: x=3(y²+z²), x=3, Ox.

12. Обчислити криволінійні інтеграли:

а) ;

б) .

Тут АВ - частина циклоїди від точки А до точки В.

13. Перейшовши до параметричного задання контура L, визначити роботу сили при переміщенні точки вздовж кривої L. Перевірити результат обчислення за допомогою теореми Стокса: .

14. Обчислити поверхневі інтеграли:

а) , - частина площини 2x-y-2z=-2, отримана в перетині з координатними площинами;

б) - зовнішня сторона поверхні x²+y² =4, що лежить між площинами z=1, z=3.

15. Знайти потік векторного поля через зовнішню сторону поверхні σ:

а) =(x+z)+(y+z)+(z-x-y), - частина поверхні x²+y²+z²=9 в перетині з площинами z=3, z=0;

б) =z-x+z, - замкнена поверхня 4z=x²+y²; z=4.

ВАРІАНТ 13

1. Знайти область визначення функції

z =.

2. Визначити похідну складеної функції за аргументом t:

z = arccos , x= sint, y = cost.

3. Знайти рівняння дотичної площини й нормалі до поверхні σ у точці м0:

σ: x²-у²-z²+xz+4x=-5, M₀(-2,1,0).

4. Перевірити, чи є функція z = f(x, y) розв`язком даного диференціального рівняння

x² -xy +y²=0 , z= + arcsin(xy).

5. Дослідити функцію z = f(x; y) на екстремум і знайти найбільше й найменше значення цієї функції в замкненій області :

z=x²+ xy-2; : y=4x²-4, y=0.

6. Змінити порядок інтегрування:

.

7. Знайти площу фігури S за допомогою подвійного інтеграла:

a) S: y= , y= x-x-;

b) S: .

8. Знайти масу пластини D з поверхневою густиною ρ:

D: x²+y²=1; x²+y²=4, x≥0, y≥0; ρ=.

9. Знайти об'єм тіла V:

z= , z = 10 - x²- y².

10. Знайти масу тіла V:

V: x²+y²+z²=9, x²+y²≤4, z≥0, ρ=2z.

11. Обчислити момент інерції однорідного тіла V щодо зазначеної осі:

V: y=x²+z², y=3, Оy.

12. Обчислити криволінійні інтеграли:

а) ;

б) .

Тут AB - частина астроїди , від точки А до точки В.

13. Перейшовши до параметричного задання контура L, визначити роботу сили при переміщенні точки вздовж кривої L. Перевірити результат обчислення за допомогою теореми Стокса: .

14. Обчислити поверхневі інтеграли:

а) , - частина площини x+3y+2z=6, отримана в перетині з координатними площинами;

б) , - внутрішня сторона поверхні x²+y²+z²=16, отримана в перетині з площиною y=0.

15. Знайти потік векторного поля через зовнішню сторону поверхні σ:

а) =x+y+xyz, - частина поверхні x²+y²=25 в перетині з площинами z=5, z=1;

б) =6x-2y-z, - замкнена поверхня z=3-2(x²+y²), z²=x²+y² (z≥0).

ВАРІАНТ 14