
[Править]Функция arccos
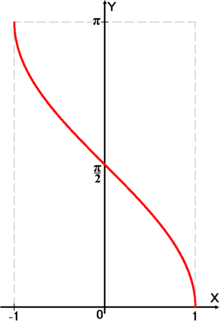
График
функции ![]() .
.
Арккосинусом числа m называется
такое значение угла x,
для которого ![]()
Функция ![]() непрерывна
и ограничена на всей своей числовой
прямой. Функция
непрерывна
и ограничена на всей своей числовой
прямой. Функция ![]() является
строго убывающей.
является
строго убывающей.
 при
при 
 при
при 
 (область
определения),
(область
определения),  (область
значений).
(область
значений).
[править]Свойства функции arccos
 (функция
центрально-симметрична относительно
точки
(функция
центрально-симметрична относительно
точки  ),
является индифферентной.
),
является индифферентной.
 при
при 
 при
при 

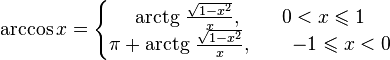



[править]Получение функции arccos
Дана
функция  На
всей своей области определения она
является кусочно-монотонной, и, значит,
обратное соответствие
На
всей своей области определения она
является кусочно-монотонной, и, значит,
обратное соответствие 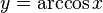 функцией
не является. Поэтому мы рассмотрим
отрезок, на котором она строго убывает
и принимает все свои значения —
функцией
не является. Поэтому мы рассмотрим
отрезок, на котором она строго убывает
и принимает все свои значения —  На
этом отрезке
На
этом отрезке  строго
монотонно убывает и принимает все свои
значения только один раз, а значит, на
отрезке
строго
монотонно убывает и принимает все свои
значения только один раз, а значит, на
отрезке 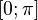 существует
обратная функция
существует
обратная функция  график
которой симметричен графику
график
которой симметричен графику 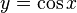 на
отрезке
на
отрезке  относительно
прямой
относительно
прямой 
[править]Функция arctg
График
функции  .
.
Арктангенсом числа m называется
такое значение угла  ,
для которого
,
для которого 
Функция  непрерывна
и ограничена на всей своей числовой
прямой. Функция
непрерывна
и ограничена на всей своей числовой
прямой. Функция  является
строго возрастающей.
является
строго возрастающей.
 при
при 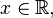
 при
при 


[править]Свойства функции arctg
 ,
при x > 0.
,
при x > 0.
 ,
при x > 0.
,
при x > 0.
[править]Получение функции arctg
Дана
функция  На
всей своей области определения она
является кусочно-монотонной, и, значит,
обратное соответствие
На
всей своей области определения она
является кусочно-монотонной, и, значит,
обратное соответствие  функцией
не является. Поэтому рассмотрим отрезок,
на котором она строго возрастает и
принимает все свои значения только
один раз —
функцией
не является. Поэтому рассмотрим отрезок,
на котором она строго возрастает и
принимает все свои значения только
один раз —  На
этом отрезке
На
этом отрезке  строго
монотонно возрастает и принимает все
свои значения только один раз,
следовательно, на интервале
строго
монотонно возрастает и принимает все
свои значения только один раз,
следовательно, на интервале  существует
обратная
существует
обратная  ,
график которой симметричен графику
,
график которой симметричен графику  на
отрезке
на
отрезке  относительно
прямой
относительно
прямой 
[править]Функция arcctg

График функции y=arcctg x
Арккотангенсом числа m называется
такое значение угла x,
для которого 
Функция  непрерывна
и ограничена на всей своей числовой
прямой. Функция
непрерывна
и ограничена на всей своей числовой
прямой. Функция  является
строго убывающей.
является
строго убывающей.
 при
при 
 при
при 


[править]Свойства функции arcctg
 (график
функции центрально-симметричен
относительно точки
(график
функции центрально-симметричен
относительно точки 
 при
любых
при
любых 

[править]Получение функции arcctg
Дана
функция  .
На всей своей области определения она
является кусочно-монотонной, и, значит,
обратное соответствие
.
На всей своей области определения она
является кусочно-монотонной, и, значит,
обратное соответствие  функцией
не является. Поэтому рассмотрим отрезок,
на котором она строго убывает и принимает
все свои значения только один раз —
функцией
не является. Поэтому рассмотрим отрезок,
на котором она строго убывает и принимает
все свои значения только один раз —  .
На этом отрезке
.
На этом отрезке  строго
убывает и принимает все свои значения
только один раз, следовательно, на
интервале
строго
убывает и принимает все свои значения
только один раз, следовательно, на
интервале  существует
обратная функция
существует
обратная функция  ,
график которой симметричен графику
,
график которой симметричен графику  на
отрезке
на
отрезке  относительно
прямой
относительно
прямой  График
симметричен к арктангенсу
График
симметричен к арктангенсу
Функция синус

|
| ||||||||
|
Область определения функции — множествоR всех действительных чисел. Множество значений функции— отрезок [-1; 1], т.е. синус функция —ограниченная. Функция нечетная:sin(−x)=−sin x для всех х ∈R. График функции симметричен относительно начала координат. Функция периодическаяс наименьшим положительным периодом 2π: sin(x+2π·k) = sin x, где k ∈ Zдля всех х ∈R. sin x = 0при x = π·k, k ∈Z. sin x > 0(положительная) для всех x ∈ (2π·k, π+2π·k), k ∈Z. sin x < 0(отрицательная) для всех x ∈ (π+2π·k, 2π+2π·k), k ∈Z.
|






