2 Алгоритмизация модели и системы
2.1 Построение логической схемы работы зоны умр
Целесообразно построить модель по блочному принципу, где каждый блок описывает некоторые достаточно простые процессы: занятие очереди, ожидание обслуживания, занятие поста, моделирование обслуживания на каком-либо посту и т.д. Причем очередность расположения блоков должна увязываться с технологическим процессом. На этом этапе целесообразно задать принятые математические соотношения в явном виде: формулы, связи, коэффициенты, параметры и т.д.
Рисунок 2.1 - Схема алгоритма моделирования работы зоны УМР
2.2 Получение математических соотношений для описания функционирования системы
Из анализа уравнения Эрланго для систем массового обслуживания с ожиданием при установившемся режиме работы, вероятности нахождения системы в состоянии:
,
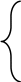
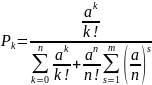при а ≤ к ≤ n
(2.1)
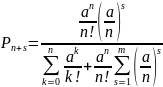при
1 ≤ s
≤ m
-
новая переменная.
Уравнения (2.2) получают путём анализа уравнения Эрландо, при котором определяется закономерность поведения вероятностей.
Вероятность отказа в обслуживании наступит при занятии всех постов и всех мест в очереди.
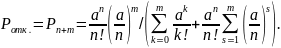(2.2)
Вероятность обслуживания будет равна:
(2.3)
Относительная пропускная способность будет равна:
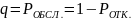(2.4)
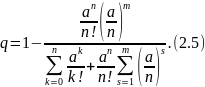
2.3 Выбор вычислительных средств для моделирования
Решение поставленной задачи обеспечивает персональный компьютер, оснащённый процессором AMD Athlon(tm) ǁ X3 445 Processor c установленной памятью 8,00 ГБ, 64-разрядной операционной системой, операционной системой Windows 7, монитором VGA.
В связи с использованием процессора с высокой тактовой частотой используем модулятор DOSbox.
Вводим команды:
mount с: с:\sim
с:
simsim
После чего модулятор DOSbox запускает программу simsim и проводим серию экспериментов.
3 Регрессионный анализ работы системы
3.1 Результаты вычислительного эксперимента
Регрессионный анализ необходим для получения математических соотношений между используемыми м модели параметрами или факторами и показателями эффективности работы системы. Необходимое число опытов N для полно-факторного эксперимента
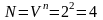(3.1)
где V – число уровней варьирования, V = 2;
n – число значимых факторов, n = 2
Составленная матрица спектра плана приведена в таблице 3.1.
Таблица 3.1 – План эксперимента
N |
X0 |
X1(λ) |
X2(μ) |
1 |
+ |
- |
- |
2 |
+ |
+ |
- |
3 |
+ |
- |
+ |
4 |
+ |
+ |
+ |
Построим
матрицу спектра плана. Для получения
и
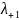изменим суточную программу соответственно
.
Для
получения значени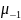й
и
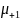изменим число рабочих, одновременно
работающих на посту (соответственно 1
и 3 человека).
Результаты расчёта сведём в таблицу 3.2.
Таблица 3.2 – Переменные модели
|
-1 |
0 |
+1 |
λ |
0,396739 |
0,521739 |
0,646739 |
μ |
0,328947 |
0,649351 |
0,961538 |
|
0,079348 |
0,104348 |
0,129348 |
|
0,065789 |
0,12987 |
0,192308 |
В соответствии с матрицей спектра плана проводим эксперимент с использованием программы «simsim.exe». Накопители, используемые в модели, не ограничиваем по ёмкости и времени ожидания. В качестве основных критериев эффективности, принимаем среднее время нахождения в системе, среднее число занятых каналов, среднее время ожидания в очереди.
При этом время моделирования Тм рассчитывалось по формуле:
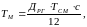(3.2)
Tм
=
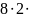
= 407 ч
В результате проведения опыта получили некоторые значения функции отклика. Представим их в таблице 3.3.
Таблица 3.3 – Матрица спектра плана и функции отклика для каждого опыта
N |
X0 |
X1(λ) |
X2(μ) |
X3(λ ∙μ) |
q |
Xз |
1 |
1 |
0,396739 |
0,328947 |
0,130506 |
0,879 |
0,928 |
2 |
1 |
0,646739 |
0,328947 |
0,212743 |
0,529 |
0,937 |
3 |
1 |
0,396739 |
0,961538 |
0,38148 |
1 |
0,332 |
4 |
1 |
0,646739 |
0,961538 |
0,621865 |
0,998 |
0,592 |
Результаты эксперимента представим в таблице 3.4.
Таблица 3.4 - Результаты эксперимента
Критерии моделирования |
Обозначение |
Единицы измерения |
1 |
2 |
3 |
4 |
Абсолютная пропускная способность |
А |
авт/ч |
0,678 |
0,631 |
0,764 |
1,275 |
Относительная пропускная способность, |
q |
авт/ч |
0,879 |
0,529 |
1 |
0,998 |
Вероятность обслуживания |
Робсл |
--- |
0,879 |
0,529 |
1 |
0,998 |
Число обслуженных автомобилей |
Nобс |
авт. |
276 |
257 |
311 |
519 |
Среднее время пребывания в системе |
tср |
ч |
39,383 |
93,763 |
0,632 |
0,925 |
Среднее время ожидания в очереди |
tож |
ч |
38,093 |
92,925 |
0,097 |
0,362 |
Среднее число занятых каналов |
Xз |
--- |
0,928 |
0,937 |
0,332 |
0,592 |
Среднее число заявок в очереди |
Xо |
--- |
29,321 |
110,899 |
0,057 |
0,393 |
Среднее число заявок в системе |
Xс |
--- |
30,249 |
11,836 |
0,390 |
0,985 |