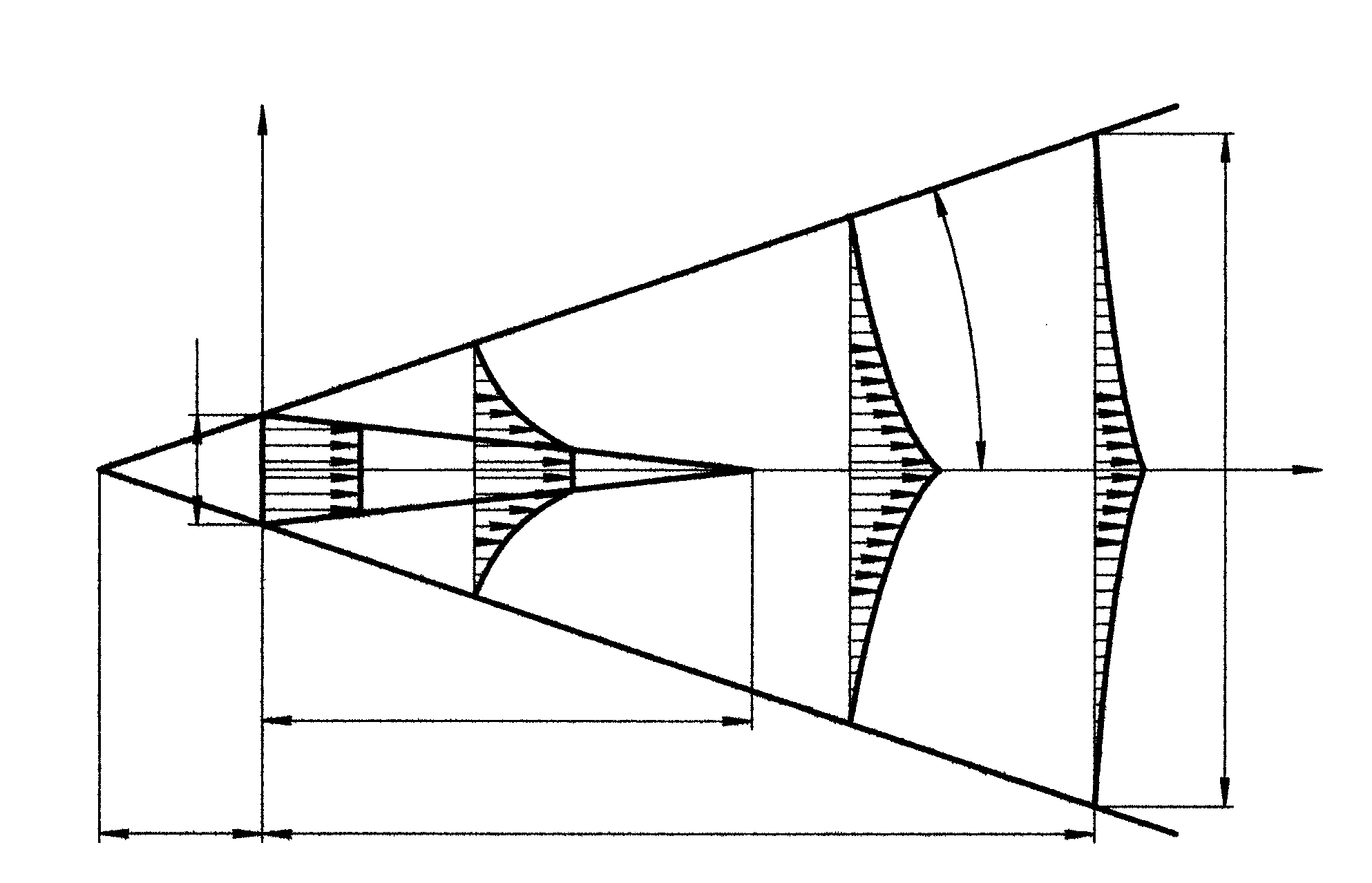
2.10.2. Затопленные струи

Движение затопленных струй теоретически и экспериментально изучалось Г. Н. Абрамовичем. На рис. 2.64 изображены схема затопленной струи и поле скоростей по ее сечению и длине.

θ

A

0

Рис. 2.64. Схема затопленной струи

Согласно схеме, струя состоит из ядра, уменьшающегося вдоль координат от до в точке А. Расстояние от отверстия до точки А называется начальным участком струи. Вокруг ядра образуется заторможенная область, расширяющаяся по ходу движения жидкости. Принято считать, что профиль скорости в ядре постоянен. Скорость в заторможенной области меняется от нуля на внешней границе струи до скорости на ее оси. Угол раскрытия струи рассчитывается по уравнению

,

где – постоянная, находится экспериментально. Для воздуха, вытекающего из круглого отверстия, 0,07÷0,08. Таким образом, угол раскрытия есть величина постоянная, не зависящая от расхода газа.

Полюсное расстояние

.

Длина начального участка

.

Диаметр струи на любом расстоянии от отверстия

.

Скорость на оси струи

где – скорость истечения из отверстия.

При истечении струи воды в воду

где

Вопросы для самоконтроля

1. Какие струи встречаются в природе и где используются струйные течения?

2. От чего зависит сила взаимодействия струи с твердой преградой?

2.11. Течение со свободной поверхностью

До сих пор предметом нашего изучения было напорное движение жидкостей. Отличительной особенностью решения задач, связанных с напорным движением, является пренебрежение влиянием силы тяжести на распределении локальных скоростей в потоке. При течении со свободной поверхностью влияние силы тяжести на характер движения становится определяющим, и градиентом давления вдоль потока в большинстве случаев можно пренебречь.

Примером безнапорного движения может служить течение жидкостей в открытых руслах, в не полностью заполненных трубах (канализационные системы), по поверхности в виде пленки и т. п. Последний случай особенно интересен для пищевой промышленности, так как пленочное течение достаточно широко распространено и ему следует уделить особое внимание, тем более что в классическом курсе гидравлики оно, как правило, не изучается.

В качестве примеров приведем пленочное течение в трубах выпарных аппаратов, оросительных конденсаторах и охладителях, в абсорберах и т. п.

Основная задача заключается в определении расхода жидкости через аппарат. Для этого необходимо найти уравнения, описывающие распределение локальных скоростей по сечению пленки, ее толщи- ну и среднюю скорость . Прежде чем перейти к решению поставленных задач, приведем некоторые понятия и определения, характерные для пленочного течения.

Объемная плотность орошения – отношение объемного расхода к смоченному периметру:

, (2.259)

откуда

. (2.260)

С учетом равенства (2.260) пленочный критерий в уравнениях (2.125) примет вид

. (2.261)

При стекании пленки жидкости по поверхности могут наблюдаться три режима течения: ламинарный, волновой и турбулентный. Ламинарный режим имеет место при ; турбулентный, по разным источникам при 1200÷1600, можно принять ориентировочно . Тогда волновой режим будет существовать при .

Теория гидродинамики стекающих пленок подробно рассмотрена в работе В. Н. Соколова и И. В. Доманского [9]. Их методики и будем придерживаться в дальнейшем.

Ламинарный режим течения пленки. Рассмотрим течение пленки жидкости по поверхности, наклоненной под углом к горизонту (рис. 2.65).

Направление движения – вдоль оси ; ось направлена нормалью к поверхности. Движение стационарное, жидкость несжимаемая. Уравнение Навье–Стокса (2.45) применительно к поставленной задаче примет вид

. (2.262)

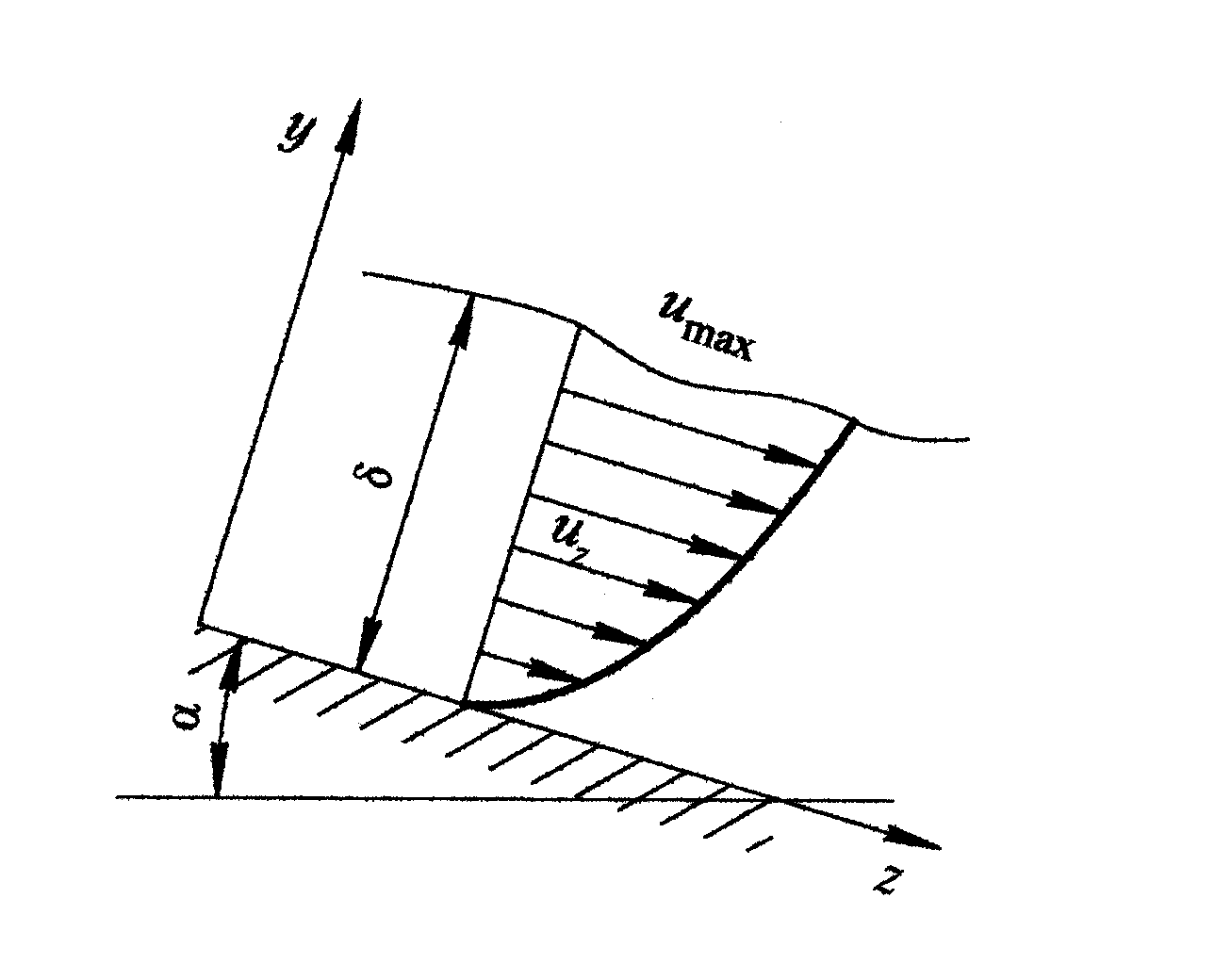
Рис. 2.65. Распределение скорости у твердой стенки

при течении жидкости со свободной поверхностью

Для пленочного течения граничные условия записываются в виде

при ; (2.263)

, (2.264)

где − касательные напряжения на внешней границе пленки (возникают в том случае, если относительно пленки движется газ (пар)); при противоточном движении жидкости и газа (пара) и при движении их в одном направлении.

Вопросы совместного движения жидкости и газа (пара) будут рассмотрены в разд. 3, здесь же ограничимся рассмотрением течения однофазной жидкости.

Если принять условие , то с учетом уравнения неразрывности (2.25) уравнение (2.262) примет вид

. (2.265)

Интегрируя дважды уравнение (2.265) при условии получим

. (2.266)

Постоянные интегрирования и найдем из граничных условий

, , тогда ;

, , тогда . (2.267)

С учетом значений и уравнение (2.266) примет вид

. (2.268)

Объемную плотность орошения, с учетом выражения (2.268), представим в виде интеграла

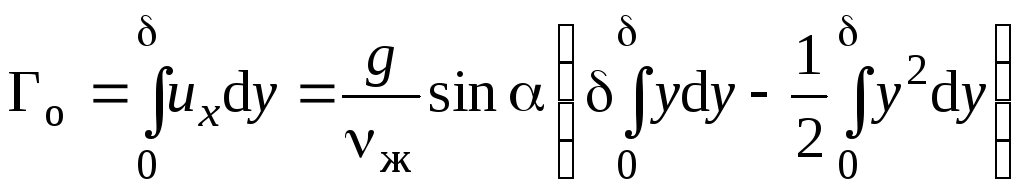. (2.269)

После интегрирования уравнения (2.269) получаем

. (2.270)

Средняя скорость течения пленки

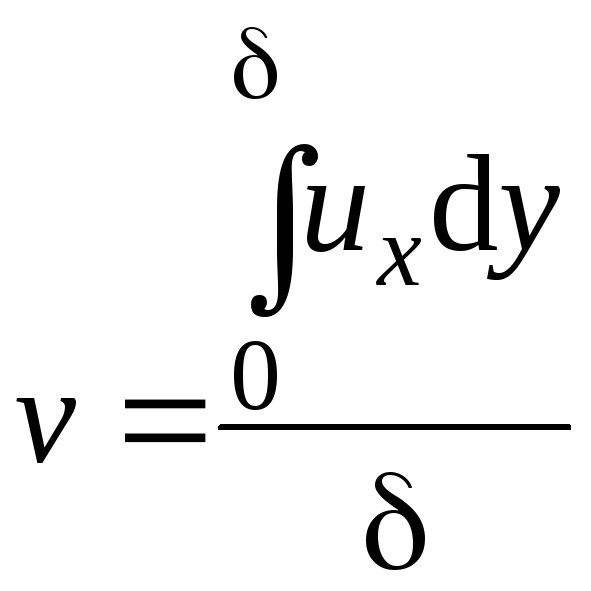. (2.271)

Подставив в уравнение (2.271) значение из уравнения (2.268) и проинтегрировав его, запишем

. (2.272)

Максимум скорости найдем из уравнения (2.268) при условии :

. (2.273)

Из уравнений (2.272) и (2.273) следует, что

(2.274)

т. е. отношение скоростей оказалось таким же, как было в плоском канале.

Толщину пленки, при заданной плотности орошения найдем из уравнения (2.270)

. (2.275)

Волновой режим течения пленки. Данный режим является переходным от ламинарного режима к развитому турбулентному. Началом волнообразования считается условие

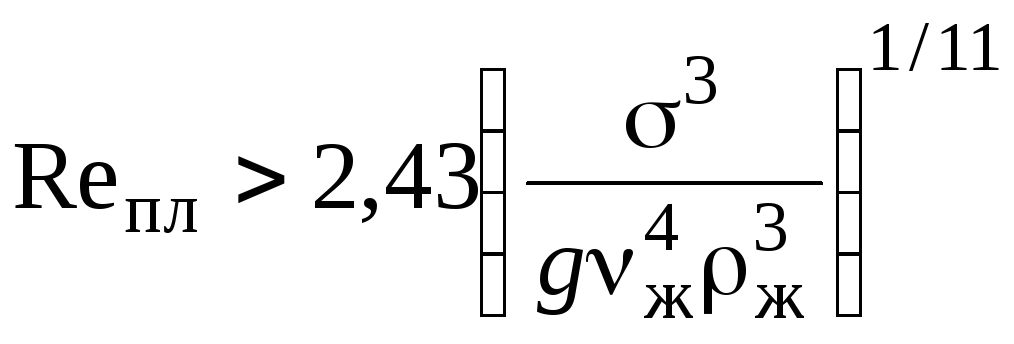. (2.276)

Толщина пленки при волновом режиме была теоретически определена П. Л. Капицей. Для вертикальной поверхности

. (2.277)

Сравнение уравнений (2.275) и (2.277) показывает, что при волновом режиме пленка лишь на 7 % тоньше, чем при ламинарном.

Турбулентный режим течения пленки. Задачу по нахождению толщины пленки, следуя работам В. Н. Соколова и И. В. Доманского, решим полуэмпирическим методом, применив модель распределения турбулентных пульсаций (2.191). Для этой цели приведем уравнение (2.269) к безразмерному виду, используя универсальные координаты и :

, (2.278)

где − безразмерная толщина пленки,

. (2.279)

Интегрирование уравнения (2.278) с учетом (2.191) дает

(2.280)

Динамическую скорость находим из уравнения (2.168), считая, что касательные напряжения уравновешиваются для однофазного потока силой тяжести пленки, т. е.

, (2.281)

тогда

, (2.282)

а

. (2.283)

Толщину пленки можно найти путем подстановки уравнения (2.279) в (2.283)

. (2.284)

Дальнейший путь определения следующий: по заданной плотности орошения из уравнения (2.280) находим значение и далее по уравнению (2.284) значение .

Задачу облегчают аппроксимацией уравнения (2.280) более простым выражением

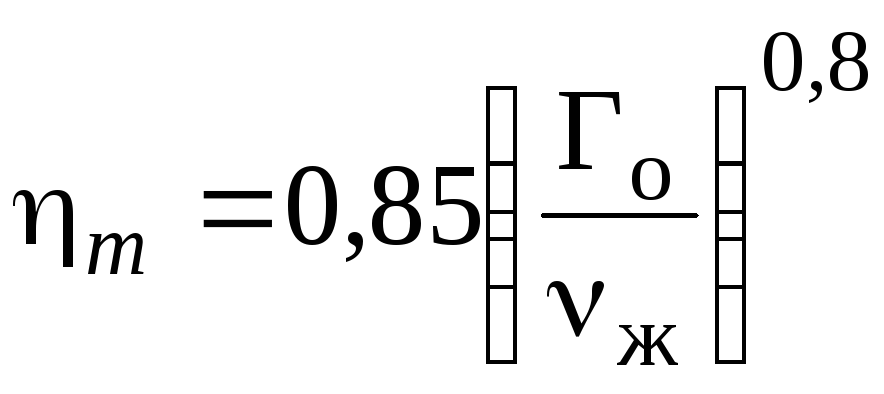. (2.285)

Подстановка зависимости (2.285) в (2.284) дает выражение

, (2.286)

справедливое при .

Выбор плотности орошения. Плотность орошения должна быть такой, чтобы вся поверхность смачивалась жидкостью, т. е. она должна быть выше некоторого минимального значения .

Для обеспечения надежной работы аппарата, независимо от режима его работы, расчет можно производить по формуле

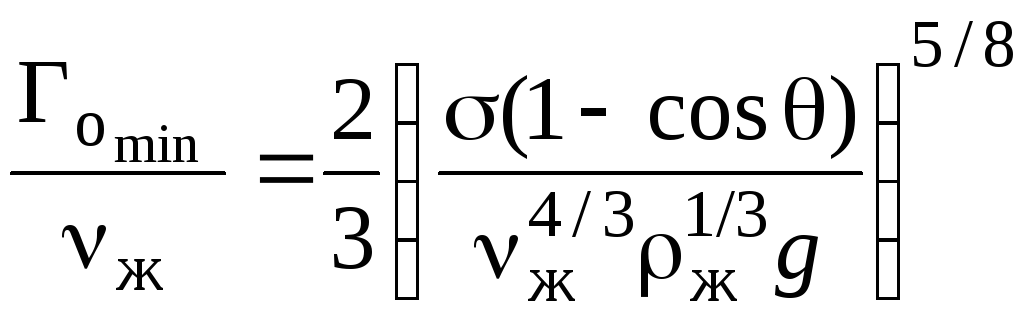, (2.287)

где − угол смачивания жидкостью сухой поверхности.

Вопросы для самоконтроля

1. В чем заключается отличие течения жидкости с открытой поверхностью от напорного?

2. Что такое объемная плотность орошения?

3. Какие режимы течения пленки встречаются в природе?

4. От чего зависит толщина пленки?