2.9. Гидравлические методы измерения расхода жидкостей

В качестве примеров гидравлического метода измерения расхода жидкостей рассмотрим наиболее часто встречающиеся типы расходомерных устройств: диафрагмы, трубы Вентури и ротаметры.

Работа устройств двух первых типов основана на измерении перепада давления в местах сужения потока.

Диафрагма представляет собой тонкую пластинку с отверстием посредине, располагаемую в трубопроводе нормалью к вектору средней скорости (рис. 2.56). При течении жидкости через отверстие происходит сжатие потока от сечения отверстия до в зоне наибольшего сужения и падение давления от до . Задача заключается в нахождении зависимости расхода жидкости от падения напо- ра . В целях ее решения составим уравнение Бернулли для сечения I и II:

. (2.252)

Согласно рис. 2.56,

. (2.253)

Из уравнения неразрывности . Учитывая, что коэффициент сжатия , а и , из уравнений (2.252) и (2.253), получим

,

откуда

, (2.254)

где 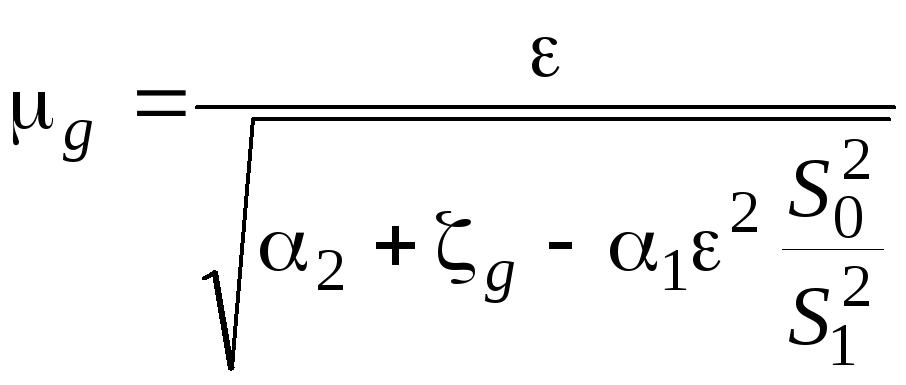– коэффициент расхода диафрагмы.

При турбулентном режиме течения можно принять

Коэффициент сопротивления диафрагмы зависит от отношения диаметров отверстия и трубопровода и определяется экспериментально.

Уравнение (2.254) обычно приводится к более простому виду

где – коэффициент дроссельного прибора при турбулентном режиме течения (при ) и заданном значении есть величина постоянная и находится опытным путем.

I

I

II

II

g

g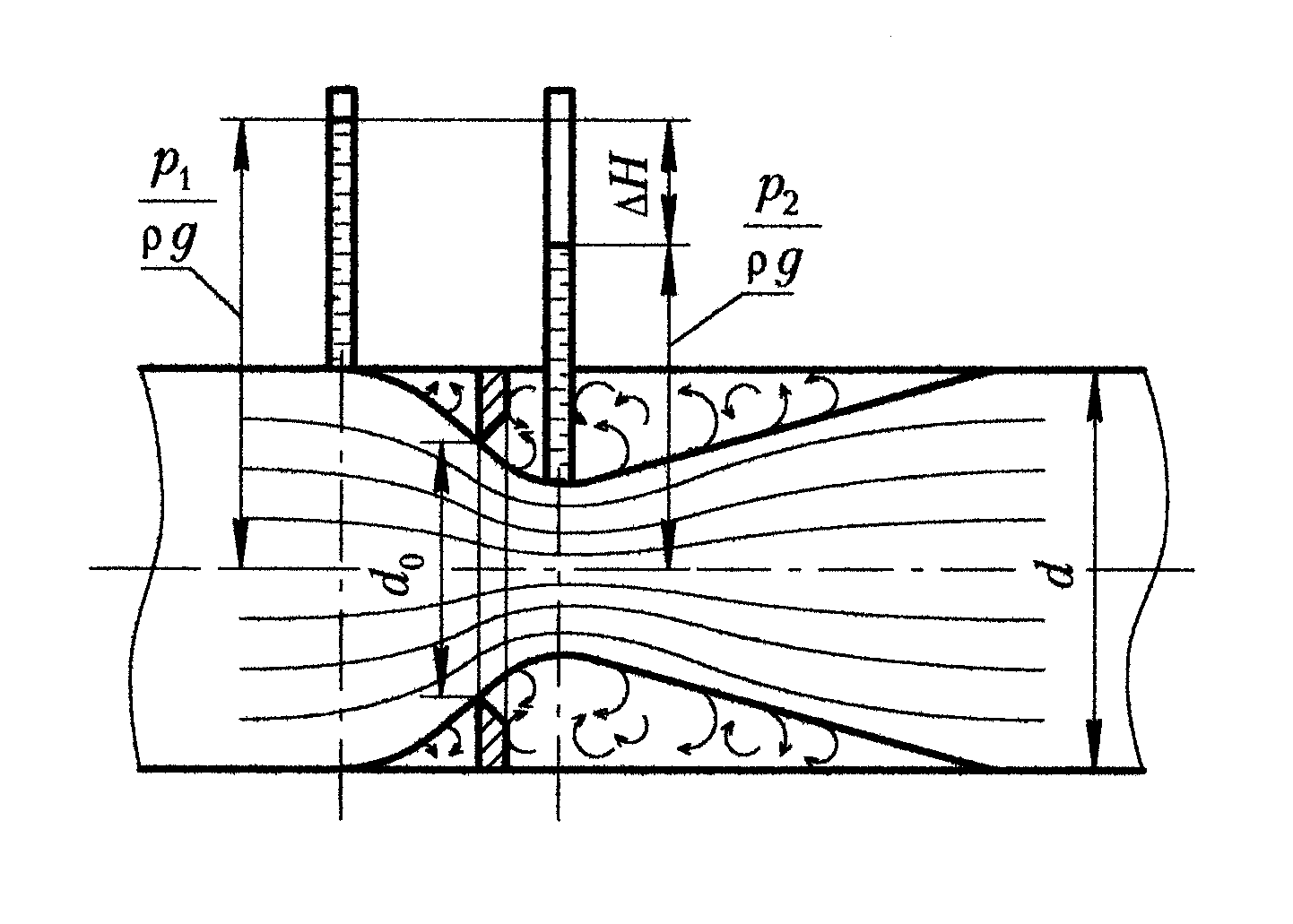

Рис. 2.56. Схема диафрагмы

Положительная сторона диафрагмы заключается в простоте конструкции. Однако она имеет значительное гидравлическое сопротивление, вызванное наличием застойных зон до и после диафрагмы, где возникают вихревые движения жидкости, которые и являются причиной высоких гидравлических потерь. Если избежать образования застойных зон, то потери напора могут быть снижены. Такие условия наблюдаются в трубах Вентури.

Труба Вентури, или двухконусный водомер, представляет собой трубу переменного сечения, состоящую из двух частей – конфузорной и диффузорной (рис. 2.57).

Отсутствие застойных зон и пренебрежение потерями напора по длине на участке между сечениями I–I и II–II позволяет записать уравнение Бернулли в упрощенной форме:

, откуда

. (2.255)

II

II

I

I

g

g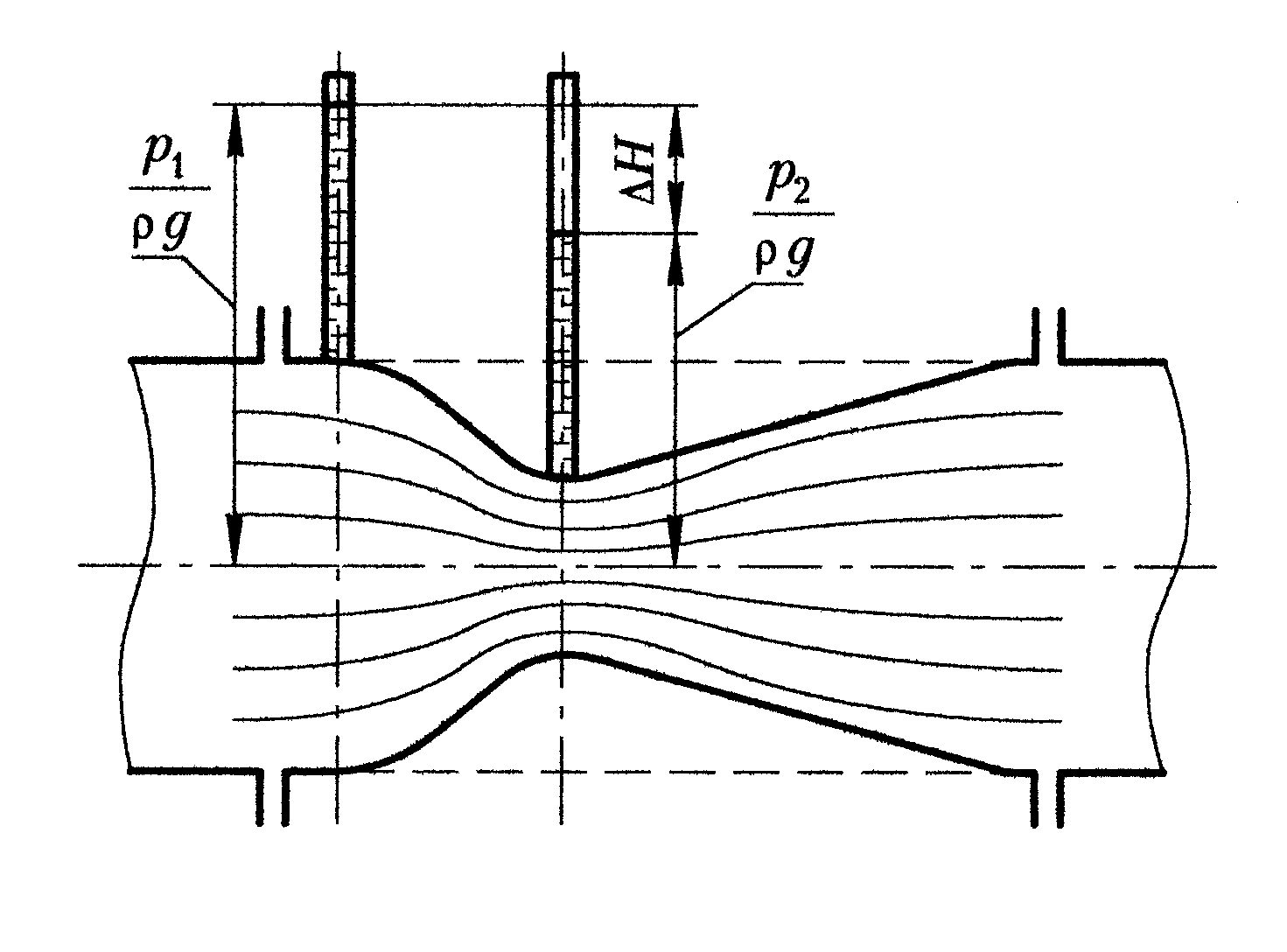

Рис. 2.57. Схема водомера Вентури

С учетом того, что и , а также , из уравнения (2.255) следует

,

где – коэффициент расхода водомера;

Коэффициент расхода водомера Вентури близок к единице.

Ротаметр представляет собой вертикально расположенную трубку, конусную внутри (рис. 2.58). В трубке имеется поплавок, на который при движении жидкости действуют три силы: лобового сопротивления Т, тяжести и подъемная

Сила лобового сопротивления будет определяться перепадом давления до и после поплавка, т. е.

,

где – площадь лобового сечения поплавка в широкой его части.

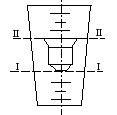
Рис. 2.58. Схема ротаметра

Подъемная сила , где – объем поплавка.

Для любого определяемого значения расхода жидкости поплавок занимает положение, при котором наступает равновесие сил:

. (2.256)

Разность давлений найдем из уравнения Бернулли, составленного для сечений I–I и II–II:

, (2.257)

где – коэффициент сопротивления кольцевого зазора между поплавком и трубкой.

Выразив через и выполнив несложные преобразования, приведем уравнение (2.257) к виду

.

Подставив полученное выражение в уравнение (2.256), получим

, (2.258)

где – коэффициент расхода ротаметра,

;

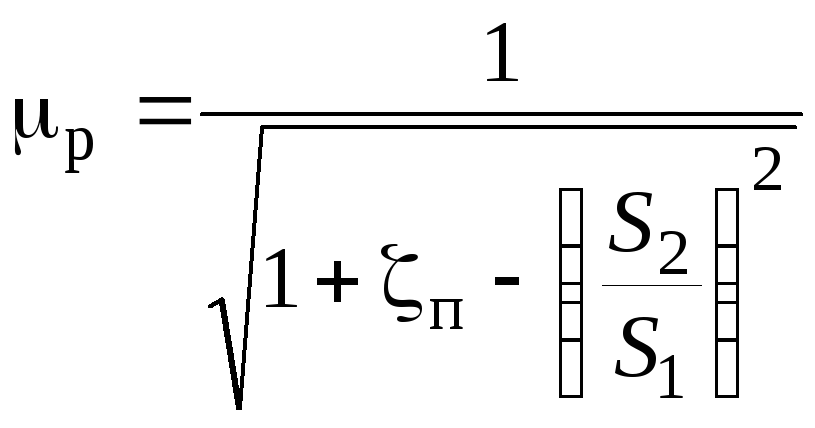для предварительных расчетов = 0,62.

Вопросы для самоконтроля

1. Какие методы измерения расхода жидкостей и газов вам известны и на чем они основаны?

2. Каково преимущество водомера Вентури перед диафрагмой и каковы его недостатки?

3. От чего зависит расход жидкости или газа через ротаметр?