Некоторые примеры инженерных расчетов

П р и м е р 1. Смазочное масло движется в зазоре подшипника скольжения (рис. 2.36). Диаметр вала м; зазор частота вращения вала ширина подшипника  м. Плотность масла ; его динамическая вязкость удельная теплоемкость = 3200 Дж/кг Объемный расход масла Определить, на сколько градусов нагреется масло при прохождении через подшипник.

Рис. 2.36. Схема подшипника скольжения

Решение. Для решения задачи необходимо определить энергию, которая выделяется за единицу времени в результате действия сил трения, т. е. найти мощность сил трения. С этой целью определяем силу трения:

Будем считать, что течение жидкости подчиняется закону Ньютона (1.6), т. е. Движение жидкости в зазоре представляет собой течение Куэтта. В первом приближении пренебрегаем перепадом давления по длине зазора, т. е. считаем Тогда, согласно выражению (2.157), уравнение (1.6) можно представить в виде

и сила трения составит

Крутящий момент силы трения

Количество теплоты, выделяющейся в результате трения, равно мощности сил трения и составляет

Так как , то

. (2.158)

Энергия, которая диссипируется в единице объема жидкости,

Из уравнения энергии (2.52) получаем

или

(2.159)

Так как во время нагрева из физических констант в наибольшей мере изменяется вязкость ( можно принять постоянными), то в равенство (2.159) необходимо ввести зависимость вязкости от температуры С учетом принятых допущений запишем

(2.160)

Разделяя переменные и интегрируя от 0 до и от до , получим

Так как – объемный расход, то

(2.161)

В первом приближении примем Подставив в уравнение (2.161) заданные в условии задачи величины, получим

град.

Поскольку температура масла повысилась ненамного, то принятое условие можно считать оправданным и результат решения град окончательным. Однако в целях поддержания температуры на заданном уровне необходимо при проектировании машины предусмотреть теплообменник для охлаждения масла в системе смазки.

П р и м е р 2. Мелассный раствор нагревается в дисковом фрикционном стерилизаторе (рис. 2.37) от температуры до Производительность стерилизатора 2,5 Число обо-ротов диска Физические свойства мелассы: зависимость вязкости от температуры имеет вид Найти геометрические размеры и , обеспечивающие нагрев жидкости до заданной температуры.

Решение. Энергия, диссипируемая в объеме жидкости, находящейся в зазоре между диском и корпусом, обусловливается в основном силами жидкостного трения от вращения диска и составляет

Рис. 2.37. Схема к расчету фрикционного стерилизатора

Крутящий момент на валу диска, с учетом двустороннего трения,

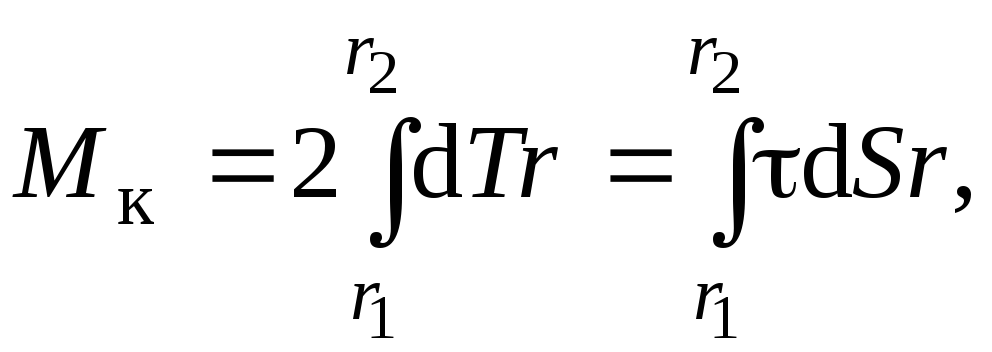
где Т – сила трения.

Так как площадь трения и касательные напряжения, как и в предыдущей задаче, равны

то

(2.162)

Проинтегрировав выражение (2.162) и выполнив несложные преобразования, получим

Мощность теплового источника

(2.163)

Из уравнения энергии (2.52)

(2.164)

Подставляя значение из уравнения (2.163) в равенство (2.164), запишем

(2.165)

Так как , а , то этим отношением можно пренебречь. Подставляя в уравнение (2.165) зависимость от и интегрируя его с учетом последнего неравенства и , получим

Отсюда

Решая задачу по исходным данным, получим

Меняя один из размеров, можно найти другой. Положим тогда

Вопросы для самоконтроля

1. Получите уравнение слоистых течений из уравнения Навье–Стокса.

2. Дайте определение канала бесконечной ширины.

3. Как связана средняя скорость течения с максимальной в каналах с прямоугольным и круглым поперечным сечением?

4. В какой степени коэффициент Дарси зависит от критерия Рейнольдса при ламинарном режиме?

5. Как выглядит эпюра скорости в канале с одной подвижной стенкой при ?