2.5. Динамика вязкой жидкости

2.5.1. Режимы течения

Различают два режима течения – ламинарный и турбулентный. Ламинарное (слоистое) течение отличается постоянством скорости и давления во времени в любой точке потока. Такое течение существует при сравнительно небольшой скорости движения жидкости. При достижении некоторого критического значения скорости происходит переход от ламинарного к турбулентному движению, которое характеризуется непрерывным изменением во времени скорости и давления в любой точке. Возникает пульсация этих параметров, в результате чего происходит интенсивное перемешивание жидкости по всему объему потока. В ходе исследований было установлено, что критическая скорость, соответствующая переходу от одного режима к другому, зависит от вязкости жидкости и диаметра трубопровода. Количественно переход от одного режима к другому определяется величиной критерия Рейнольдса . Толкование физического смысла критерия Рейнольдса будет дано в следующем подразделе, отметим лишь, что при движении жидкости в трубопроводах общего назначения в качестве критического значения критерия Рейнольдса, при котором происходит смена режимов течения, принимается величина . На практике наиболее часто принято считать, что при в трубопроводах имеет место ламинарный режим течения, а при – турбулентный режим. Конечно, столь резкой границы смены режимов течения в природе не существует. Переход от одного режима к другому происходит в некотором диапазоне изменения .

Течение вязкой жидкости в общем виде описывается уравнениями (2.42)–(2.44), несжимаемой жидкости – уравнением (2.46).

При решении задач гидродинамики турбулентных потоков вводятся понятия осредненных значений составляющей скорости и напряжения . Тогда их локальные значения

где и – пульсационные составляющие скорости и напряжения.

В проекциях на координатные оси (ограничимся осью 0x) получаем

Полагая, что уравнения движения в напряжениях могут быть пригодны для описания турбулентных течений, после введения в уравнение (2.38) осредненных параметров, получим в проекции на координатную ось из уравнения (2.39)

(2.116)

где

Аналогичные уравнения можно записать для осей 0y и 0z. Эти уравнения получены О. Рейнольдсом и носят его имя.

Уравнения Рейнольдса и неразрывности потока образуют незамкнутую систему, так как в нее входят шесть неизвестных пульсационных составляющих, для нахождения которых требуются дополнительные уравнения. Законы распределения турбулентных пульсаций будут рассмотрены в подразд. 2.5.8.

2.5.2. Гидродинамическое подобие

Различают геометрическое, кинематическое и динамическое подобие потоков. Геометрическое подобие заключается в подобии сходных геометрических размеров; кинематическое – в подобии скоростных полей; динамическое – в подобии силовых полей. Последнее подобие невозможно без выполнения первых двух.

Соблюдение условий подобия необходимо при моделировании машин, аппаратов и процессов, происходящих в них. Исследуя модель и используя условия подобия, можно перенести результаты исследований на реальный объект.

Условия гидродинамического подобия можно получить из уравнений (2.45), приводя их к безразмерному виду. Для этого введем безразмерные величины, выразив их через соответствующие масштабы: L – масштаб длины, – масштаб скорости, – масштаб времени, – масштаб массовых сил, – масштаб давления. В этом случае безразмерные величины будут таковы:

(2.117)

В формулах (2.117) индексом «=» обозначены безразмерные параметры.

Ограничиваясь осью , преобразуем уравнение (2.45) с учетом формул (2.117); сократив его стороны на отношение , получим уравнение движения в безразмерном виде:

(2.118)

Вошедшие в уравнение (2.118) безразмерные коэффициенты являются критериями подобия, которые названы именами известных ученых, внесших большой вклад в развитие науки о движении жидких сред:

(2.119)

где St – критерий Струхаля; Fr – критерий Фруда; Eu – критерий Эйлера; Re – критерий Рейнольдса.

Для подобных процессов одноименные критерии подобия должны быть равными.

Для сжимаемой жидкости критерий Эйлера имеет вид

Критерии подобия имеют вполне определенный физический смысл и выражают отношение определяющих сил, действующих в потоке: St – соотношение сил инерции, вызванных локальными и конвективными ускорениями; Eu – отношение сил давления к силам инерции; Re – отношение сил инерции к силам вязкого трения; Fr – отношение сил инерции к массовым силам.

Критерии подобия можно получить не прибегая к операции приведения дифференциальных уравнений движения жидкости к безразмерному виду. Это можно сделать проще, взяв соотношения любых сил, действующих в потоках, как в однофазных, так и многофазных.

Рассмотрим влияние сил инерции и сил трения . Запишем, чему равны эти числа:

;

,

где m − масса элемента жидкости; V − его объем; − плотность; a − ускорение; S − площадь трения.

Перейдем от равенств к пропорциональностям, введя характерные величины L, U, t:

; .

Определим отношение сил:

.

Таким образом мы получили критерий Рейнольдса.

П р и м е р. Получить критерий подобия, характеризующий взаимоотношение сил инерции и сил поверхностного натяжения. Такие взаимодействия имеют место на поверхности раздела жидкость–газ, например движение жидкой струи в газовой среде, движение газовых пузырьков в жидкости. Эти вопросы мы рассмотрим несколько позднее.

Решение. Определим силы. Мы уже установили, что . Сила поверхностного натяжения .

Отношение сил

называется критерием Вебера.

Выбор линейного размера в критериях подобия зависит от постановки задачи. Независимо от вида движения при решении задач гидродинамики вводятся понятия гидравлического радиуса и эквивалентного диаметра в качестве характерных геометрических размеров. Под гидравлическим радиусом понимают отношение площади затопленного поперечного сечения трубопровода, через который протекает жидкость, к смоченному периметру П:

. (2.120)

Отсюда, например, для круглого трубопровода диаметром получается

(2.121)

Выражая через , имеем . Диаметр, выраженный через гидравлический радиус, называется эквивалентным диамет- ром . Поэтому из уравнений (2.120) и (2.121) следует

(2.122)

Таким образом, исходя из формул (2.120) и (2.122), например, для трубопровода прямоугольного живого сечения со сторонами и получаем

(2.123)

Уравнение (2.123) можно представить в ином виде:

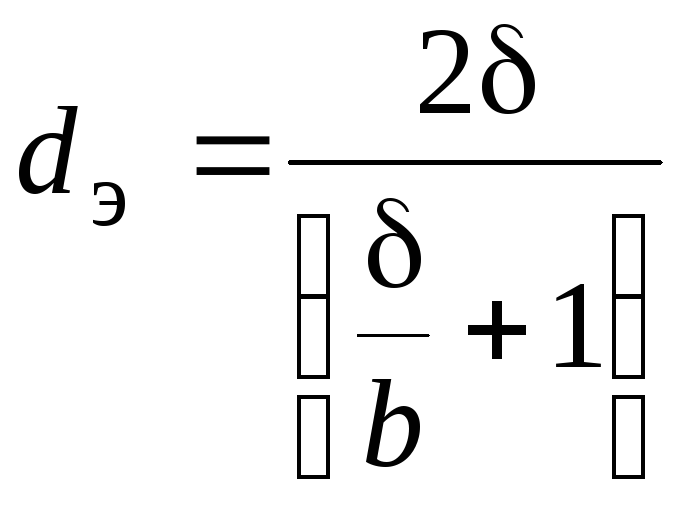. (2.124)

При ; канал, удовлетворяющий этому условию, называется каналом бесконечной ширины.

При стекании жидкости по поверхности в виде пленки толщиной площадь ее поперечного сечения . Подставив значе- ние в равенство (2.122), получим .

Можно легко доказать, что для трубопровода с круглым поперечным сечением . Таким образом, эквивалентный диаметр равен диаметру гипотетического трубопровода круглого сечения, для которого отношение площади к смоченному периметру П имеет то же значение, что и для трубопровода некруглого сечения. Введение понятий позволяет унифицировать многие расчеты в задачах движения жидкостей.

При продольном обтекании потоком тонкого профиля за характерный размер принимается его длина . За масштаб скорости при движении жидкости в каналах принимается средняя скорость , при обтекании тонких профилей − скорость набегающего потока . С учетом сказанного критерий Рейнольдса может принимать следующие виды:

; . (2.125)