2.4.6. Теорема н.Е. Жуковского о подъемной силе
Одной из важнейших
задач гидромеханики, решаемой на основе
модели потенциального течения идеальной
жидкости, является задача о силовом
взаимодействии произвольного профиля
с обтекающим его потоком. С подобными
течениями приходится сталкиваться при
обтекании жидкостями и газами лопаток
рабочих колес лопастных насосов,
гидравлических и газовых турбин, крыльев
летательных аппаратов и т. п. Решения
задач подобного рода основаны на теореме
Н.Е. Жуковского, которая формулируется
следующим образом: если поток, имеющий
в бесконечности скорость
,
обтекает контур и циркуляция
скорости по этому контуру равна Г, то
равнодействующая сила давления жидкости
на контур равна произведению скорости
потока в бесконечности, циркуляции
скорости и плотности жидкости
.
Для доказательства теоремы рассмотрим
произвольный профиль в плоском потоке,
ограниченном контрольной линией
в виде окружности (рис. 2.28). За пределами
этого контура возмущения, вносимые
профилем в поток, бесконечно малы, т. е.
радиус окружности контрольной линии
.
Рис. 2.28. Обтекание профиля потоком жидкости
Потенциал скорости представляют в виде
суммы двух потенциалов
,
где
– потенциал скорости за пределами
контура. Тогда из уравнений (2.96) следует
;
(2.109)
,
где
− потенциал скорости возмущенного
движения жидкости внутри контура.
При
имеет место
;
;
;
и 
.
Выделим на контрольной поверхности
бесконечно малую площадку
,
где
– ширина профиля цилиндрической
контрольной поверхности в плоскости,
перпендикулярной плоскости рисунка
(см. рис. 2.28). На эту элементарную площадку
действует элементарная сила
,
проекции которой на координатные оси
;
.
Массовый расход жидкости через элементарную площадку
(2.110)
Подставив в равенство (2.110) значения
и
из уравнений (2.109) и отнеся расход к
единице ширины профиля
,
запишем
. (2.111)
Во всех дальнейших выводах силы, действующие на профиль и контрольную поверхность, так же как и расход, будут отнесены к длине профиля.
Применим к контрольной поверхности
теорему об изменении количества движения,
согласно которой изменение количества
движения в единицу времени
массы жидкости, прошедшей через
контрольную поверхность в единицу
времени, равно главному вектору сил,
действующих на эту массу, т. е.
,
где
– вектор изменения количества движения;
– вектор равнодействующей силы;
– вектор силы, действующей на профиль;
– вектор силы, действующей на контрольную
поверхность со стороны потока жидкости.
В проекциях на координатные оси
;
.
С учетом уравнений (2.109)
;
.
Наша задача заключается в определении
силы
.
Найдем ее проекции на координатные оси:
(2.112)
.
Ранее мы уже доказали (см. подразд.
2.4.5), что сила сопротивления при обтекании
цилиндра потоком идеальной жидкости
.
То же самое имеет место для любого
профиля. Таким образом, нам предстоит
определить силу
.
Давление
находим из уравнения Бернулли (2.76) при
условии
:
.
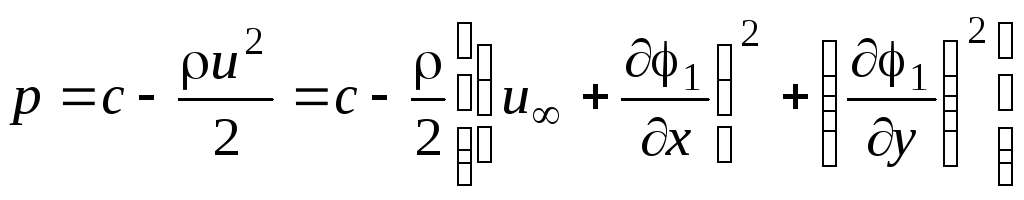Пренебрегая значениями
и
,
как величинами второго порядка малости,
запишем
. (2.113)
Подставив значение
из (2.111),
– из (2.113) в уравнение (2.112), с учетом
(2.109), получим
(2.114)
Преобразуя равенство (2.114) и помня, что
,
как величина второго порядка малости
и
,
получаем
или
Согласно уравнению (2.18), интеграл
есть
циркуляция скорости Г по контуру
,
следовательно,
. (2.115)
Вектор скорости
,
повернутый на 90о в сторону,
противоположную направлению циркуляции,
указывает направление действия подъемной
силы
.
Если вектор скорости совпадает с
направлением оси
,
циркуляция направлена по часовой стрелке
(Г < 0), тогда
положительна.
Вопросы для самоконтроля
1. Связь между какими силами устанавливает уравнение движения идеальной жидкости?
2. Напишите уравнение Бернулли для элементарной струйки для несжимаемой и сжимаемой идеальной жидкости.
3. Объясните геометрический и энергетический смысл слагаемых уравнения Бернулли.
4. В чем заключается различие в движении сжимаемого и несжимаемого газа в каналах разных форм при дозвуковом и сверхзвуковом течении?
5. Изобразите линии тока при безвихревом обтекании цилиндра потоком жидкости с циркуляцией и без циркуляции скорости.
6. В чем заключается парадокс Даламбера?
7. Сформулируйте теорему И.Е. Жуковского о подъемной силе.