
Тишин ВБ Новоселов АГ Процессы переноса в технолог аппаратах
.pdf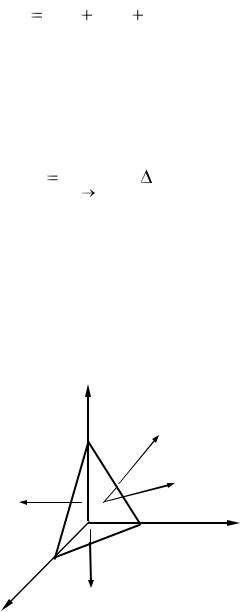
Через проекции на координатные оси вектор |
|
может быть |
|||
F |
|||||
представлен в виде |
|
|
|
|
|
|
|
|
|
|
|
F Fxi Fy j Fz k , |
|
|
|||
где i, j, k – единичные векторы.
Поверхностные силы пропорциональны площади поверхности, на которую они действуют. Напряжение сил на площадке с нормалью n определяется равенством
|
|
pn |
lim ( P/ S ). |
|
S 0 |
Рассмотрим напряжения, возникающие в элементе жидкости, в виде тетраэдра (рис. 1.4). Напряженное состояние будет определяться суммой массовых и поверхностных сил. Оценим их порядок. Массовые силы dRm ~ ρ  dV ~ ρ
dV ~ ρ  dxdydz , поверхностные −
dxdydz , поверхностные −
dP ~ dS ~ dxdy , т. е. dRm на порядок меньше dP, поэтому массовыми силами пренебрегаем.
z
p y
pn
px
х
pz
y
Рис. 1.4. Напряженное состояние элемента жидкости
Таким образом, мы будем рассматривать напряженное состоя-
ние элемента жидкости под действием только поверхностных сил. |
||
|
|
|
Напряжение этих сил pn выразим через составляющие, совпадающие |
||
|
|
|
с направлением осей координат, как px , py и |
pz . |
|
Напряженное состояние будет определяться суммой массовых и поверхностных сил. Оценим их порядок. Массовые силы
21

dRm ~ 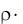 dV ~
dV ~  dxdydz , поверхностные − dP ~ dS ~ dxdy , т. е. dRm на порядок меньше dP. Поэтому массовыми силами пренебрегаем.
dxdydz , поверхностные − dP ~ dS ~ dxdy , т. е. dRm на порядок меньше dP. Поэтому массовыми силами пренебрегаем.
При произвольном расположении площадки с внешней норма- |
|||
|
|
|
|
лью n вектор pn может быть представлен в виде равенства |
|||
|
|
|
|
pn |
pnx cos(n, ^ x) |
pny cos(n, ^ y) |
pnz cos(n, ^ z), |
или в проекциях на координатные оси:
pnx |
σ xcos(n, ^ x) |
τ xycos(n, ^ y) |
τ xzcos(n, ^ z); |
pny |
τ yxcos(n, ^ x) |
σ ycos(n, ^ y) |
τ yzcos(n, ^ z); |
pnz |
τ zxcos(n, ^ x) |
τ zy cos(n, ^ y) |
σ z cos(n, ^ z) , |
где и  − нормальная и касательная компоненты напряжения.
− нормальная и касательная компоненты напряжения.
В качестве примера на рис. 1.5 показаны направления компонентов напряжений в плоскости z0x
z
z
|
|
zx |
|
|
|
|
xz |
|
|
|
|
x |
|
x |
|
xz |
|
|
|
0 |
zx |
|
x |
|
|||
|
|
||
z
Рис. 1.5. Нормальные и касательные напряжения в элементарном объеме жидкости
Таким образом, вектор напряжения pn определяется девятью скалярными величинами ( x , y , z , xy , xz , yx, yz , zx , xy ) и может быть выражен тензором напряжений
22

|
σ x τ xy τ xz |
|
|
T |
τ yx σ y τ yz |
. |
(1.12) |
|
τ zx τ zy σ z |
|
|
Между матрицами (11) и (1.12) существует прямая зависимость, выражающая закон внутреннего трения для ньютоновских жидкостей:
|
|
|
|
|
T |
2 . |
|
|
|
|
|
|
|
В проекциях на координатные оси это равенство примет вид |
|||||||||
уравнений (1.17) и (1.18). |
|
|
|
|
|
|
|||||
|
|
Примем условие симметричности тензора (1.12) относительно |
|||||||||
главной |
диагонали. |
Тогда |
xy |
yx ; |
yz |
zy ; |
zx |
xz |
|||
и |
x |
y |
z |
const. |
Таким образом, |
напряжение |
определяется |
||||
|
|
|
|
|
|
|
|
|
|||
только шестью скалярными величинами. В покоящейся жидкости, согласно уравнению (1.6), касательные напряжения равны нулю. То-
гда, |
pnx |
xcos(n, ^ x), |
pny |
ycos(n, ^ y), |
pnz |
zcos(n, ^ z), |
но |
||
pnx , |
pny , pnz |
есть проекции |
|
на соответствующие оси, т. |
е. |
||||
pn |
|||||||||
|
|
|
z . Давление в произвольной точке покоящейся сре- |
||||||
pn |
x |
y |
|||||||
ды, |
равное |
p |
pn |
x |
y |
z , не |
зависит |
от ориентации |
|
площадки в пространстве. В этом заключается важнейшее свойство гидростатического давления.
Давлением в движущейся жидкости постулируется величина
|
p |
|
1 |
( |
|
|
|
z ). |
(1.13) |
|
|
x |
y |
||||||
|
|
3 |
|
|
|
|
|
||
|
Для нормальных напряжений эта связь выражается в виде ра- |
||||||||
венства (по оси 0x ) |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
ux |
|
(1.14) |
|
|
x |
p |
2 |
|
|
div u, |
|||
|
x |
||||||||
|
|
|
|
|
|
|
|||
|
|
|
|
|
|
|
|
||
где |
и – динамические коэффициенты вязкости, причем коэффи- |
||||||||
циент |
относится только к сжимаемой жидкости. |
|
|||||||
23

Суммируя нормальные напряжения x , y , z , запишем
|
|
|
|
(1.15) |
x |
y |
z |
3 p (2 3 )div u . |
|
|
|
Для соблюдения равенства (1.13) необходимо, чтобы в уравне-
ниях (1.14) и (1.15)
2 |
. |
(1.16) |
|
3 |
|||
|
|
Тогда нормальные составляющие тензора T можно представить следующим образом:
x
y
z
|
|
|
ux |
2 |
|
|
|
p |
2 |
|
|
|
|
div u; |
|
x |
3 |
|
|||||
|
|
|
|
|
|||
|
|
|
uy |
2 |
|
(1.17) |
|
p |
2 |
|
|
|
|
div u; |
|
|
y |
3 |
|||||
|
|
|
|
|
|||
|
|
|
uz |
2 |
|
|
|
p |
2 |
|
|
|
|
div u. |
|
|
z |
3 |
|
||||
|
|
|
|
|
|||
Касательные напряжения выражаются уравнениями
xy |
|
ux |
|
|
uy |
; |
|
||
|
y |
|
x |
|
|||||
|
|
|
|
|
|||||
|
|
|
|
|
|
||||
yz |
|
uy |
|
|
uz |
|
; |
(1.18) |
|
|
z |
|
y |
|
|||||
|
|
|
|
|
|||||
|
|
|
|
|
|
||||
zx |
ux |
|
uz |
. |
z |
|
x |
||
|
|
|||
|
|
|
Уравнения (1.18) выражают обобщенный закон течения Ньютона. Они определяют поток импульса силы трения (количества движения) в единицу времени через единицу площади трущихся поверхностей. Для случая одномерного движения, приведѐнного на рис. 1.2, уравнения (1.18) приобретают вид (1.7).
24

1.2.3. Уравнение движения в напряжениях
Вывод уравнения основан на законе изменения количества движения применительно к массе жидкости, заключенной в объеме V: изменение количества движения в единицу времени равно главному вектору сил, действующих на элемент жидкости:
|
|
|
|
|
|
dK |
(1.19) |
||||
R |
Rm |
P. |
|||
|
|||||
dt |
|||||
|
|
|
|
Количество движения можно представить в виде интеграла
|
|
(1.20) |
K |
udV . |
V
Изменение количества движения связано с изменением векто-
ра скорости u во времени. Тогда из предыдущего уравнения
|
|
|
|
dK |
|
du |
dV . |
|
|
|
|
dt |
V |
dt |
|
|
|
|
|
Главный вектор поверхностных сил
|
|
|
P |
pndS |
div pndV . |
|
S |
V |
(1.21)
(1.22)
Подставляя уравнения (1.11), (1.21), (1.22) в равенство (1.19) и суммируя подынтегральные функции с учетом произвольности
объема V , получим |
|
|
|
|
|
|
|
||
|
du |
(1.23) |
||
|
|
F |
div pn . |
|
|
dt |
|||
|
|
|
|
В проекциях на координатные оси уравнение движения в напряжениях (1.23) примет вид
ρ |
dux |
ρF |
σx |
|
τxy |
|
τxz |
; |
(1.24) |
|
|
|
|
|
|
||||
|
dt |
x |
x |
|
y |
|
z |
|
|
|
|
|
|
|
|
25

ρ |
duy |
ρF |
τ yx |
|
|
σ y |
|
|
τ yz |
; |
(1.25) |
||||||
|
|
|
|
|
|
|
|
|
|
|
|
||||||
|
|
dt |
y |
x |
|
|
y |
|
|
z |
|
|
|
||||
|
|
|
|
|
|
|
|
|
|
|
|||||||
ρ |
|
duz |
ρF |
|
τzx |
|
|
τzy |
|
|
σz |
. |
|
(1.26) |
|||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||
|
|
dt |
z |
x |
|
|
y |
|
|
z |
|
|
|
||||
|
|
|
|
|
|
|
|
|
|
|
|||||||
1.2.4.Уравнения движения вязкой сплошной среды
Вобщем виде уравнения движения могут быть получены путем подстановки уравнений (1.17) и (1.18) в выражения (1.24)–(1.26).
Впроекциях на координатные оси получим
ρ |
dux |
|
|
ρFx |
|
|
|
|
p |
|
2 |
|
|
|
|
|
μ |
|
|
ux |
|
|
|
|
|
|
|
|
|
|
μ |
|
|
ux |
|
|
u y |
|
|
|||||||||||||||||||||
|
|
dt |
|
|
|
|
|
x |
|
x |
|
|
x |
|
|
|
|
|
|
|
|
|
|
|
y |
x |
|
|||||||||||||||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
y |
|
|
|
||||||||||||||||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
ux |
|
|
|
|
uz |
2 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
μ |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
( |
|
|
div u); |
|
|
|
|
|||||||||||||
|
|
|
|
|
|
|
|
z |
|
|
z |
|
|
|
|
|
x |
3 |
|
|
|
|
x |
|
|
|
(1.27) |
|||||||||||||||||||||||||||||||||
ρ |
|
du y |
|
ρFy |
|
|
|
p |
|
2 |
|
|
|
|
μ |
|
u y |
|
|
|
|
|
|
|
|
|
|
|
|
μ |
|
|
u y |
|
|
ux |
|
|||||||||||||||||||||||
|
|
dt |
|
|
|
|
y |
y |
|
y |
|
|
|
|
|
|
|
|
|
|
|
|
|
x |
y |
|
||||||||||||||||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
x |
|
|
|
||||||||||||||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
ux |
|
|
|
|
uz |
2 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
μ |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
( |
|
|
div u) ; |
(1.28) |
||||||||||||||||||||
|
|
|
|
|
|
|
|
z |
|
|
|
z |
|
|
|
|
|
x |
3 |
|
|
|
|
y |
|
|
||||||||||||||||||||||||||||||||||
|
|
|
duz |
|
ρFz |
|
|
p |
|
2 |
|
|
|
|
μ |
|
uz |
|
|
|
|
|
|
|
|
|
|
|
μ |
|
|
uz |
|
|
ux |
|
|
|||||||||||||||||||||||
|
|
|
dt |
|
|
|
z |
z |
|
z |
|
|
|
|
|
|
|
|
|
|
|
|
x |
z |
|
|||||||||||||||||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
x |
|
|
|
|||||||||||||||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
uz |
|
|
|
|
u y |
2 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
μ |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
( |
|
|
div u). |
|
|
|
(1.29) |
||||||||||||||||||||||||
|
|
|
|
|
|
|
|
y |
|
|
y |
|
|
|
|
|
z |
3 |
|
|
|
|
z |
|
|
|
|
|
||||||||||||||||||||||||||||||||
Уравнения (1.27)–(1.29) выражают баланс количества движения потока жидкости в общем виде.
26

Из уравнений (1.27)–(1.29) следует несколько частных реше- |
|||||||||||||||||
ний. Если |
const и среда несжимаема, |
|
|
|
|
0 . После деления |
|||||||||||
то div u |
|||||||||||||||||
уравнений (1.27)–(1.29) на запишем |
|
|
|
|
|
|
|||||||||||
|
|
dux |
|
F |
1 |
|
|
|
p |
ν |
2 |
u |
x |
; |
|
||
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||
|
|
dt |
|
x |
ρ |
|
x |
|
|
|
|
|
|||||
|
|
|
|
|
|
|
|
|
|
|
|||||||
|
|
duy |
|
F |
1 |
|
|
p |
ν |
2u |
|
; |
(1.30) |
||||
|
|
|
|
|
|
|
|
|
|
|
y |
||||||
|
|
|
|
|
|
|
|
|
|
|
|||||||
|
|
dt |
|
y |
|
ρ |
|
y |
|
|
|
|
|
||||
|
|
|
|
|
|
|
|
|
|
|
|
||||||
|
|
duz |
|
Fz |
1 |
|
|
|
p |
|
ν |
2 |
uz . |
|
|||
|
|
dt |
|
ρ |
|
z |
|
|
|||||||||
|
|
|
|
|
|
|
|
|
|
|
|||||||
Выразим полную производную через частные. Для краткости ограничимся одномерным потоком в направлении оси x :
|
dux |
|
|
ux |
|
ux |
|
|
ux |
|
|
u y |
|
ux |
|
uz |
ux |
|
. |
(1.31) |
|||||||||||
|
|
dt |
|
|
t |
|
|
x |
|
|
|
y |
z |
||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||||||||
В векторной форме система уравнений (1.30) примет вид |
|
||||||||||||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
2 |
|
|
||||
|
|
u |
|
|
|
|
|
|
|
|
|
1 |
|
|
|
|
|
|
|
|
|
|
|||||||||
|
|
|
|
u grad u |
|
F |
|
|
|
|
|
|
|
grad p |
ν |
u, |
|
(1.32) |
|||||||||||||
|
|
t |
|
|
|
|
|
|
ρ |
|
|||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||
где 2 – оператор Лапласа, |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||
|
|
|
|
|
|
2 |
|
|
|
2 |
|
|
|
|
|
2 |
|
|
|
2 |
|
|
|
|
|
|
|
||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
. |
|
|
|
|
(1.33) |
||
|
|
|
|
|
|
|
|
|
|
x2 |
|
|
|
y2 |
|
|
|
z2 |
|
|
|
|
|||||||||
При отсутствии сил трения из уравнения (1.32) следует урав- |
|||||||||||||||||||||||||||||||
нение движения идеальной жидкости: |
|
|
|
|
|
|
|
|
|
|
|
||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
1 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
du |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||
|
|
|
|
|
|
|
|
|
|
|
F |
|
|
|
|
|
grad p. |
|
|
|
|
(1.34) |
|||||||||
|
|
|
|
|
|
|
dt |
|
|
|
|
|
ρ |
|
|
|
|
|
|||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||
В случае статического |
равновесия u |
0 |
и уравнение (1.34) |
||||||||||||||||||||||||||||
примет вид |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||
|
|
|
|
|
|
|
|
|
|
1 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||
|
|
|
|
|
|
|
|
F |
|
|
|
grad p . |
|
|
|
|
(1.35) |
||||||||||||||
|
|
|
|
|
|
|
|
|
|
ρ |
|
|
|
|
|||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
27 |
|
|
|
|
|
|
|
|
|
|
|
|
||

Уравнения движения идеальной жидкости гидростатики (1.34) и (1.35) носят имя Эйлера.
Уравнение (1.32), называемое уравнением Навье–Стокса, по сути своей выражает второй закон Ньютона и устанавливает связь между массовыми и поверхностными силами, отнесѐнными к единице массы жидкости. Слагаемые в нем имеют размерность ускорения
и характеризуют величину сил, действующих в потоке жидкости.
Первое слагаемое левой части du/dt представляет собой уско-
рение элемента жидкости, вызванное изменением скорости во времени; второе – ускорение, вызванное изменением скорости элемента жидкости в пространстве при перемещении его из одной точки пространства в другую и называемое конвективным ускорением. Оба
слагаемых определяют величину сил инерции. |
|
|
|
|
||
|
Слагаемые в правой |
части равенства |
(1.32) выражают: |
|||
|
– силы давления; |
ν |
2 |
|
– силы вязко- |
|
F – массовые силы; 1/ grad p |
|
u |
||||
го трения.
При решении задач гидрогазодинамики с использованием уравнения Навье–Стокса необходимо задание краевых условий, из которых отметим два:
1) нормальная к твердой поверхности составляющая скорости
un 0;
2) касательная составляющая скорости равна скорости движения самой поверхности.
Уравнения Навье–Стокса (1.27)–(1.29) не являются замкнутой системой, поэтому к ним необходимо добавить уравнения зависимости плотности и вязкости от температуры и уравнение неразрывности потока (1.4). Уравнения Навье–Стокса понадобятся нам при решении целого ряда задач, связанных с динамикой движения жидких сред.
Однако, прежде чем переходить к решению частных задач, основанных на уравнении Навье–Стокса, необходимо познакомиться с законом сохранения энергии применительно к движущейся жидкости.
1.3. Уравнение энергии
При движении жидкости соблюдается закон сохранения и пре-
вращения энергии, который может быть сфоpмулиpован следующим
образом: изменение во времени полной энергии E в объеме среды
28

равно сумме мощности N всех внешних сил, приложенных к объему, и теплового потока Qт , т. е.
|
|
|
|
dE |
N Qт . |
(1.36) |
|
|
|||
dt |
|||
|
|
Полная энергия складывается из кинетической и потенциальной (внутренней) энергий. Для гомогенной жидкости, без изменения агрегатного состояния,
|
ρu |
2 |
|
E |
|
dV c TρdV ; |
|
|
|
||
|
2 |
|
v |
V |
|
V |
|
|
|
|
|
|
|
|
u2 |
|
dE |
|
d |
ρ |
ρc T dV . |
||
|
|
|
|
|
||
dt |
|
dt V |
|
2 |
v |
|
|
|
|
||||
Мощность внешних сил
N Nm NS ,
где Nm и NS – мощность массовых и поверхностных сил, причем
Nm
NS uPS
|
|
|
|
uRm |
uFρdV ; |
|
|
|
V |
|
|
|
|
|
|
upndS |
|
div ( pnu)dV . |
|
S |
V |
|
|
В общем случае подведенная теплота складывается из конвективного и радиационного потоков:
Qт Qк Qр ,
где
Q |
dT |
dS ( grad T ) |
|
dS |
div ( grad T )dV ; |
|
n |
||||
к |
dn |
|
|
|
|
S |
S |
|
|
V |
|
|
|
|
|||
|
|
29 |
|
|
|

Qр  qрdV ,
qрdV ,
V
здесь qр – плотность радиационного теплового потока. Суммируя Qк и Qр , получим
Qт div( grad T )dV |
qрdV . |
V |
V |
Подставим значения полученных величин в уравнение (1.36). Отнеся значения энергий к единице объѐма элемента жидкости и суммируя подынтегральные функции, имея в виду, что при отсутствии изменения агрегатного состояния теплоѐмкость при постоянном объѐме равна теплоѐмкости при постоянном давлении (cV = cp), запишем
|
d |
|
u2 |
|
|
(1.37) |
||
ρ |
|
|
|
c pT |
ρuF |
div( pu) div(λ grad T ) ρqр , |
||
dt |
2 |
|||||||
|
|
|
|
|
||||
где c p – удельная теплоемкость при постоянном давлении.
При отсутствии теплообмена с окружающей средой слагаемые div( grad T) и qp равны нулю. В этом случае из уравнения (1.37)
следует
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||
|
|
|
d |
|
|
|
|
du |
|
|
|
(upx ) |
(upy ) |
|
(upz ) |
|
|
|
|
|
|
|||||||||||||||||||||||
|
|
ρ |
|
(c pT ) uFρ |
|
ρu |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||
|
|
dt |
|
dt |
|
|
|
|
x |
|
|
|
|
|
y |
|
|
|
|
|
|
z |
|
|
|
|
|
|
||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||||||
|
|
|
du |
|
|
p |
|
p |
|
p |
|
|
|
u |
|
|
|
u |
|
|
u |
|
|
|
||||||||||||||||||||
|
|
|
uFρ ρu |
|
|
|
|
u |
|
|
|
u |
|
|
|
|
|
u |
|
|
|
|
|
px |
|
|
|
|
py |
|
|
|
|
pz |
|
. |
|
|
||||||
|
|
|
dt |
|
|
x |
|
y |
|
z |
|
x |
|
y |
z |
|
|
|||||||||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||||||||||||
|
|
После перегруппировки слагаемых запишем |
|
|
|
|
|
|
|
|
|
|
||||||||||||||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||||
|
d |
|
|
|
u |
|
|
px |
|
|
|
|
py |
|
|
|
|
pz |
|
|
|
|
u |
|
|
|
|
u |
|
|
u |
|
||||||||||||
ρ |
|
(c pT ) |
u ρ |
|
|
|
ρF |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
px |
|
|
|
py |
|
|
pz |
|
. |
||||||||||
dt |
|
t |
|
|
x |
|
|
|
|
y |
|
|
|
|
z |
|
x |
|
y |
z |
||||||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||||||||
30
