Тишин ВБ Новоселов АГ Процессы переноса в технолог аппаратах

не менее жаркая дискуссия, чем при выборе явного вида функции / ( ) .

Остановимся кратко на работах, связанных с исследованиями по нахождению турбулентных чисел Прандтля, и выясним, насколько обоснованно применение аналогии при решении задач тепло- и массообмена в турбулентных средах.

Пожалуй, наиболее полные сведения собраны и систематизированы в работе S. Sideman и W. Pinczewski [32], согласно которой численные значения Prt лежат в пределах от 0,1 до 2,5. Правда, данные различных авторов, приведѐнные в этой работе, в основном относятся к жидким металлам и газам, у которых Pr 1. Что касается жидкостей, то здесь следует обратить внимание на результаты исследований Говена и Смитта, установивших, что для жидкостей с чис-

лами Pr 5,7 143 Prt 0,8 0,9 .

С.С. Кутателадзе с сотрудниками [4], изучая влияние полимерных добавок на гидравлические потери и теплообмен, определили значения Prt по изменению профиля температур по сечению турбулентного потока. В результате было установлено, что по мере удаления от стенки Prt снижается от 1,6 до 0,9.

Несомненный интерес представляют работы Р.З. Адинберга, Дильмана и М. Jusclie [9], в которых приводятся уравнения для расчѐта Prt .

В первом случае турбулентное число Прандтля зависит только от числа Pr :

1

во втором случае – не только от Pr , но и от критерия Рейнольдса:

Анализ представленных работ показывает близость результатов различных авторов и позволяет сделать вывод о том, что значения Prt близки к единице, поэтому нет никаких оснований отвергать

аналогию, как и метод решения задач тепло- и массообмена. Хотя следует признать, что полной аналогии, конечно, нет. Но этот недостаток компенсируется тем, что решения задач на основе аналогии носят полуэмпирический характер и требуют эмпирического определения коэффициентов пропорциональностей, которые и нивелируют допущенные упрощения.

Таким образом, учитывая всѐ сказанное выше, мы имеем полное право при решении различных задач тепло- и массообмена принять турбулентное число Прандтля равным единице.

До сих пор разговор шѐл о тепло- и массообмене между твѐрдой стенкой и движущимся вдоль неѐ турбулентным потоком. При тепло- и массообмене между турбулентной средой и находящимися в ней газовыми пузырьками или каплями жидкости их поверхность может деформироваться под действием турбулентных пульсаций и являться дополнительным источником турбулентности, характеризуемым параметром межфазной турбулентности f в уравнении (4.40). В дальнейшем будем рассматривать в основном газожидкостные потоки, основные понятия и определения которых даны в подразд. 2.6.

142

5. РЕШЕНИЕ ЗАДАЧ ТЕПЛО- И МАССООБМЕНА НА ОСНОВЕ АНАЛОГИИ МЕЖДУ ПЕРЕНОСОМ КОЛИЧЕСТВА ДВИЖЕНИЯ И ТЕПЛОТЫ И МАССЫ

Решение рассматриваемых задач будет сводиться к получению уравнений для расчѐта коэффициентов тепло- и массообмена на ос-

нове уравнений (4.37), (4.38), (4.40).

При расчѐте тепло- и массообменных аппаратов используют средние значения коэффициентов переноса. Они могут быть получены из уравнений (4.32) и (4.33). После их преобразования получим

Уравнения (5.1) и (5.2) можно представить в привычном безразмерном виде, выбрав предварительно характерный (определяющий) размер.

В случае теплообмена между теплопередающей поверхностью теплообменных элементов и омывающей еѐ средой в качестве характерного размера выбирают диаметр аппарата da . Уравнение (5.1) можно записать в безразмерном виде:

пропорциональный радиусу аппарата, т. е.

и сплошной фазами за характерный размер рекомендуется принимать линейное значение масштаба турбулентности элемента дисперсной

143

фазы Lt . Каждый автор по-своему подходит к выбору характерного

размера. Одни авторы чаще всего прибегают к наиболее простому варианту, принимая за характерный линейный размер масштаба турбулентности усреднѐнное значение диаметра дисперсной фазы dд .

В этом случае уравнение для вычисления безразмерного максимального масштаба турбулентности будет выглядеть аналогично уравне-

нию (5.4):

Другие авторы для расчѐта характерного размера предлагают пользоваться уравнениями, в которые, кроме размера дисперсной фазы, входят еще и гидродинамические параметры. Для определения характерного размера дисперсной фазы в системе газ–жидкость в литературе встречаются уравнения вида (2.125). В таком случае максимальный масштаб турбулентности при исследовании тепло- и массообмена между культуральной средой и элементами дисперсной фазы в безразмерном виде можно выразить зависимостью

ется различием гидродинамических условий взаимодействия между дисперсной и сплошной фазами.

Ранее уже говорилось, что поверхность пузырей может деформироваться (колебаться) под действием турбулентных пульсаций. Причѐм линейный масштаб турбулентных пульсаций, деформирующих поверхность, будет тем больше, чем больше расстояние между пузырями. С увеличением газосодержания расстояние между пузырями уменьшается, в связи с чем снижается и вероятность деформации поверхности. Можно сказать, что отношение (1 г ) / г в равен-

144

стве (5.6) характеризует условия стесненности пузырей в турбулентной среде.

С клетками дело обстоит несколько иначе. Во-первых, поверхность клетки, в отличие от пузыря, не испытывает деформаций.

ше газосодержания. Поэтому условия стесненности не сказываются на скорости теплообмена и массообмена между клеткой и культуральной жидкостью.

С учѐтом предыдущих рассуждений запишем уравнения для определения тепловых и диффузионных критериев Нуссельта:

– при обмене между пузырѐм и жидкостью

– при обмене между клеткой и средой

Максимальный масштаб турбулентности для пузырей рассчитываем по уравнению (5.6), для клеток – по уравнению

Средние безразмерные разности температур и концентраций

иm можно вычислить как средние интегральные величины:

145

Подставив зависимость (5.16) в уравнение (5.3), получим

Уравнения (5.16) и (5.17) пригодны для расчѐта коэффициентов теплообмена при движении как однофазных, так и многофазных потоков в любых аппаратах, так как они получены на основе общих положений полуэмпирической теории турбулентного переноса.

Попытаемся решить ряд конкретных задач, связанных с конвективным переносом теплоты в различных теплообменных аппаратах, с помощью математической модели, полученной на основе аналогии.

5.1. Теплообмен между потоком однофазной жидкости и гладкой теплопередающей поверхностью

5.1.1. Теплообмен в каналах с различной формой поперечного сечения

Теплообмен в трубах с круглым поперечным сечением. Ре-

шение задачи конвективного теплообмена между турбулентным потоком жидкости и теплопередающей поверхностью трубчатых теплообменников на основе аналогии между переносом импульса и теплоты, наиболее простое.

Обработка экспериментальных данных по теплообмену при движении в трубах однофазных [9, 10] и многофазных потоков позволила установить численные значения коэффициентов пропорциональности и показателей степеней в уравнениях (5.16) и (5.17).

Основным источником турбулентности в трубах является стенка, а величина турбулентных пульсаций будет определяться касательными напряжениями на стенке, которые рассчитываются по уравнению

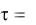
w8 2 . (5.19)

Значение динамической скорости найдѐм из уравнения (2.68)

известным в гидравлике формулам. Считая трубы гидравлически гладкими, запишем

Таким образом, мы установили связь между максимальным масштабом турбулентности и критерием Re. Если принять за границу перехода от турбулентного режима течения к ламинарному значе-

148

ленных турбулентными пульсациями, и сил вязкости не только в однофазных потоках, но и многофазных. Только при mкр < 87 говорить

следует не о ламинарном течении, а о вязкостно-турбулентном, в котором силы вязкости играют первостепенную роль в формировании профиля скорости по сечению потока.

В дальнейшем будем полагать, что в многофазных потоках изменение турбулентных пульсаций подчиняется тем же законам, что и в однофазных.

После подстановки уравнения (5.23) в уравнение (5.18) полу-

чим

Уравнение (5.25) по виду схоже с уравнением Михеева (4.3). Примерно такого же вида уравнения можно найти в работе [8]. Строго говоря, показатель степени при Pr величина переменная и зависит

Следует обратить внимание на отсутствие в уравнении (5.25) параметра, учитывающего направление теплового потока, как это сделано в уравнении (4.3) и др. Это связано с тем, что выбор или расчѐт физических свойств жидкостей производится при температуре стенки. Кроме того, при турбулентном режиме движения среды, с чем мы и будем в дальнейшем иметь дело, отношение средней вязкости к вязкости у стенки близко к единице и ею можно пренебречь

5.1.2.Теплообмен при движении жидкостей

вгофрированных каналах пластинчатых аппаратов

Данная задача несколько сложнее предыдущей. Однако она представляет несомненный интерес, так как пластинчатые аппараты широко распространены в различных отраслях микробиологической и пищевой промышленности. Их расчеты сводятся к определению поверхности теплообмена и гидравлических сопротивлений, для чего используются эмпирические уравнения, позволяющие рассчитать коэффициенты теплообмена и гидравлического сопротивления у .

Множество типов пластин предопределило и соответствующее количество эмпирических зависимостей для расчета и у .

149

Наиболее полные сведения по таким зависимостям можно найти в работе [27], изданной более тридцати лет тому назад. Однако к настоящему времени различными фирмами выпущены теплообменники, скомпонованные из пластин c иными формами гофр, но ка- ких-либо сведений об уравнениях, необходимых для их расчетов, в литературе нет.

Провести экспериментальные исследования по теплообмену для получения необходимых зависимостей непосредственно на предприятиях, эксплуатирующих такие аппараты, практически невозможно, но измерить гидравлическое сопротивление вполне доступно. В связи с указанными обстоятельствами представляет интерес вывод уравнения, которое позволяло бы рассчитывать коэффициенты в каналах с любыми формами гофр, или, по крайней мере, для пластин сетчато-поточного типа в «елку», наиболее часто встречающихся на пищевых предприятиях, имея для этого лишь данные по исследованию гидродинамики.

Следует сказать, что сама по себе эта идея не нова. Подобные решения можно найти в работах [4, 30], однако непосредственно об уравнениях, пригодных для расчета пластинчатых аппаратов, в них речь не идет.

В своем решении будем опираться на работу [30], в которой обобщены результаты исследований по теплообмену в аппаратах, различающихся по конструкции и принципам действия. Решение задачи основано на уравнении (5.3).

Уравнение (5.3) приводится, применительно к пластинчатым аппаратам, к следующему виду:

ный диаметр канала.

Безразмерное расстояние от стенки до оси канала (максимальный масштаб турбулентности)

150