А27848 Тишин ВБ Процессы переноса в технол аппаратах

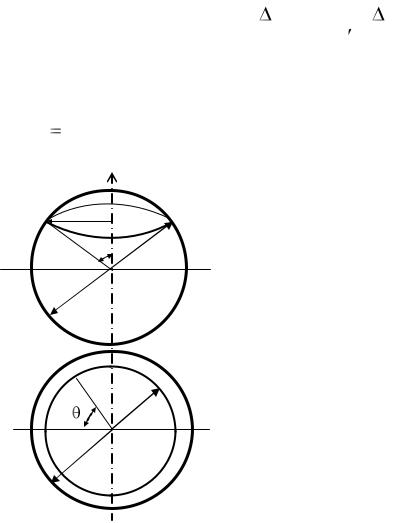
Другие два автора также используют основные положения теории турбулентности, но решение их основано на дифференциальном уравнении колебания поверхности пузыря под действием турбулентных пульсаций жидкости и является более строгим. Поэтому его и рассмотрим.

2.6.5. Определение параметра межфазной турбулентности

Рассмотрим поток газожидкостной смеси при пузырьковом режиме течения. Допустим, что объѐм жидкости V массой m движется в турбулентной среде с пульсационной скоростью u , ударяется в поверхность пузыря и деформирует ее до тех пор, пока кинетическая энергия жидкости станет равной нулю, а потенциальная − максимальной. В этом положении участок деформируемой части ПКФ будет иметь размеры r R (рис. 2.10).

y

R

α

dп

r

R

Рис. 2.10. Скорость пульсаций поверхностей пузыря

Далее под действием сил поверхностного натяжения поверхность пузыря стремится принять прежнюю форму. Однако сила инерции жидкости вновь приводит ПКФ в движение, и процесс по-

81

вторяется. Возникшие колебания поверхности будут затухать под действием вязких сил. Можно предположить, что дробление пузыря произойдет в момент достижения амплитуды колебаний некой максимальной величины. Таким образом, задачу можно свести к решению дифференциального уравнения колебаний круглой мембраны в вязкой среде [11]:

Уравнение (2.100) устанавливает связь между силами, действующими на пузырь, отнесенными к единице массы жидкости. Применительно к конкретно решаемой задаче слагаемое в левой части характеризует силы инерции, возникающие в результате изменения направления вектора скорости, связанного с колебанием поверхности пузыря. В правой части равенства слагаемое в скобках определяется упругими свойствами поверхности раздела фаз и характеризует силы поверхностного натяжения, а слагаемое с отрицательным знаком – силу вязкого трения.

Задаваясь граничными и начальными условиями

из уравнения (2.100) получим

82

Численные значения ak и bk найдем согласно начальным условиям. При колебании неподвижными (узловыми) являются точки,

Уравнение (2.102) дает нам значение амплитуды колебания (пульсаций) точек, лежащих на поверхности пузыря, ограниченной радиусом R :

Из уравнений (2.102) и (2.103) можно получить безразмерное значение амплитуды в виде зависимости

Величина f есть параметр межфазной турбулентности, и уравнения (2.104) и (2.105) определяют закон его изменения во времени.

При изучении процессов массопереноса, как правило, определяют средние значения диаметров пузырей и коэффициентов массообмена, поэтому необходимо найти среднее значение параметра

до t tт и от r 0 до r R . Величина tт характеризует время, кото-

рое проходит между двумя воздействиями на ПКФ турбулентных пульсаций (или время пребывания вихря у ПКФ), и может быть найдена как

83

Для вычисления интеграла функции Бесселя воспользуемся формулами Ньютона–Котеса. В результате получим

Проинтегрировав (2.116) с учетом (2.114), (2.115), (2.117),

находим

Сумма экспонентных функций в круглых скобках выражения (2.118) есть сумма членов геометрической прогрессии со знаменателем, поэтому запишем

где q1 − частота собственных колебаний ПКФ.

86

Вывод уравнения (2.120) приведѐн в сокращѐнном виде. Желающие получить более подробную информацию о решении представленной задачи могут обратиться к работе [9].

Частота собственных колебаний ПКФ

Скорость распространения волн по поверхности пузыря A определяется ее упругими свойствами, зависящими от поверхностного натяжения и плотности жидкости. Тогда из условий размерности следует записать

где c1 sin / c − коэффициент, определяемый экспериментально. Строго говоря, эта величина переменная, так как угол 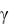зави-

сит от силы воздействия турбулентных пульсаций на поверхность пузыря, поэтому при решении каждой конкретной задачи должен быть определен отдельно.

Согласно работам [12, 13], пульсационную скорость можно выразить в виде зависимости

87

В вопросе о выборе масштаба турбулентности единого мнения нет. Нами при решении данной задачи, для расчѐта масштаба турбулентности, принято уравнение, представленное в работе [9] (там же дана ссылка на первоисточник), так как оно в конечном итоге обеспечило наилучшую сходимость с опытными данными:

Подставляя уравнение (2.125) в (2.124), получим зависимость для определения пульсационной скорости:

Силу сопротивления среды колебанию ПКФ и частоту δ определим по данным работы [13]:

В уравнении (2.100) слагаемое, характеризующее силу сопротивления, представим в виде пропорциональности

В таком случае из (2.127) и (2.128) следует

где с2 − коэффициент пропорциональности.

Подставив уравнения (2.121)−(2.129) в равенство (2.120) и пренебрегая для маловязких жидкостей влиянием сил трения, получим выражение для определения осреднѐнной величины межфазной турбулентности в виде зависимости

88

2.6.6. Определение диаметра пузырей

Значение диаметра пузыря, образующегося после дробления, найдѐм из следующих соображений. Предположим, что дробление пузырей происходит под воздействием динамического напора турбулентных пульсаций. При этом величина у в уравнении (2.102) достигает максимального значения, равного диаметру на момент дробления пузыря.

Величину ymax определим, исследовав уравнение (2.102) на максимум. Приравняв к нулю выражение (2.105), получим значе-

Анализ уравнения (2.132) показал, что изменение коэффициента с2 в широком интервале не влияет на значение dп . По данным ра-

боты [13] рекомендуется с2 = 30. Исходя из этого влиянием экспоненты можно пренебречь; равенство (2.132) с учетом (2.121), (2.126) и (2.129) примет вид

В уравнении (2.133) значение коэффициента с1 определялось на основе экспериментальных данных по измерению среднего диа-

89

метра пузырей в аппаратах с различными системами аэрации [9]. В барботажных аппаратах колонного типа за основу определения с1 в уравнении (2.133) были взяты данные из работ [14, 15]. Этот выбор диктовался тем, что авторы K. Akita и F. Ioshida провели исследования по измерению размеров пузырей в барботажной колонне методом фотографирования в различных жидкостях в широком диапазоне изменения их физических свойств. Кроме того, одновременно измеря-

Этими же авторами было предложено уравнение для расчѐта диаметра пузырей:

Вычисленные по уравнению (2.135) значения диаметра пузырей подставляли в уравнение (2.133), откуда затем определяли коэффициент c1 . Входящую в уравнение (2.133) величину Е найдем из

уравнения (5.43) – см. разд. 5.

В результате обработки экспериментальных данных указанных работ было установлено, что коэффициент c1 не является величиной

постоянной и несколько зависит от размеров аппарата и физических свойств жидкости, слабо – от газосодержания. Для согласования опытных данных и уравнения (2.133) потребовалась необходимость представления c1 в виде зависимости

Отсутствие в уравнении (2.133) вязкости жидкости и появление еѐ в полученном равенстве вполне понятно, так как при его выводе мы ею пренебрегли. Однако причиной появления в нѐм значи-

90