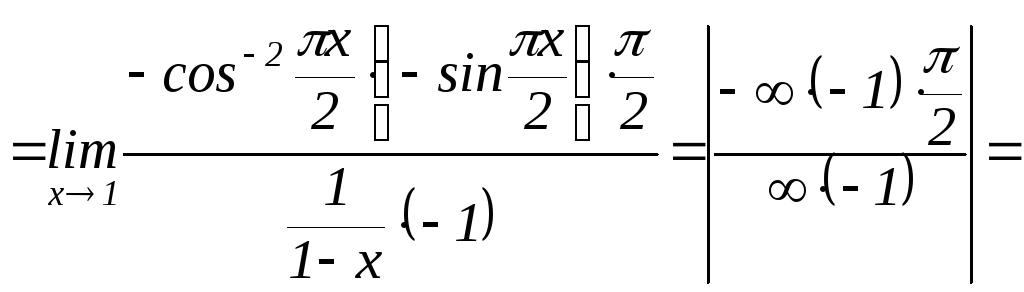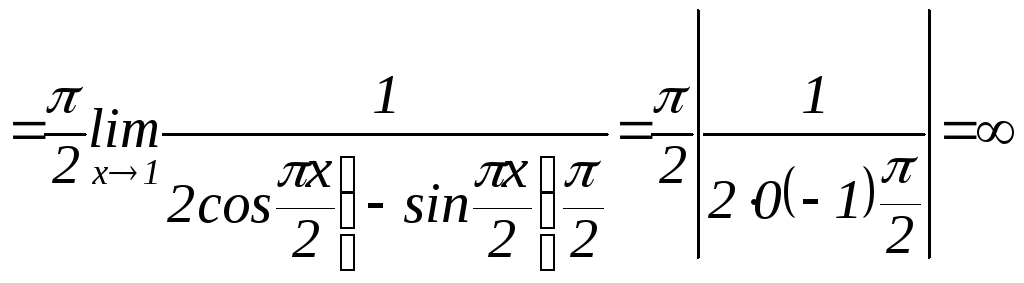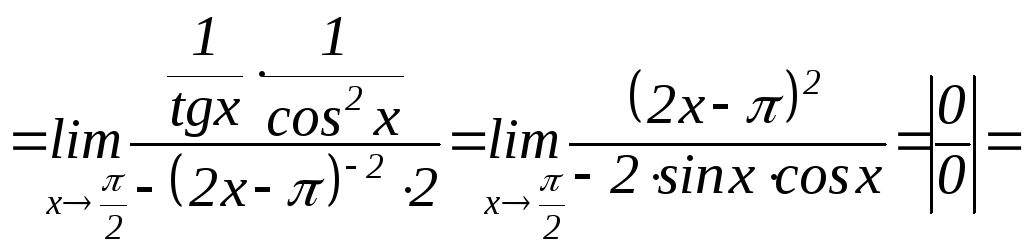Вычисление пределов по правилу Лопиталя

- Правило Лопиталя для вычисления пределов с неопределенными выражениями видаилиможно сформулировать в виде теоремы.

 - Теорема. Пусть однозначные функции идифференцируемы в некоторой окрестности точки, причем. Тогда, если существует предел (конечный или бесконечный) отношения производных этих функций, то существует равный ему предел отношения самих функций.

 - Обратите внимание: именно существование предела отношений производных гарантирует существование предела отношения функций, но не наоборот! Предел отношения функций может существовать и при отсутствии предела отношения производных.

Однако на практике это правило применяют в обратном порядке: предел отношения функций приравнивают пределу отношения производных.

Пример – иллюстрирует случай неприменимости правила Лопиталя.

Пусть , найдем пределы отношения функций: ;

и их производных: - не существует.

Правило Лопиталя применять нельзя.

 - и

• Правило Лопиталя можно применять несколько раз подряд, если неопределенность после очередного применения не раскрыта.

• Неопределенные выражения вида 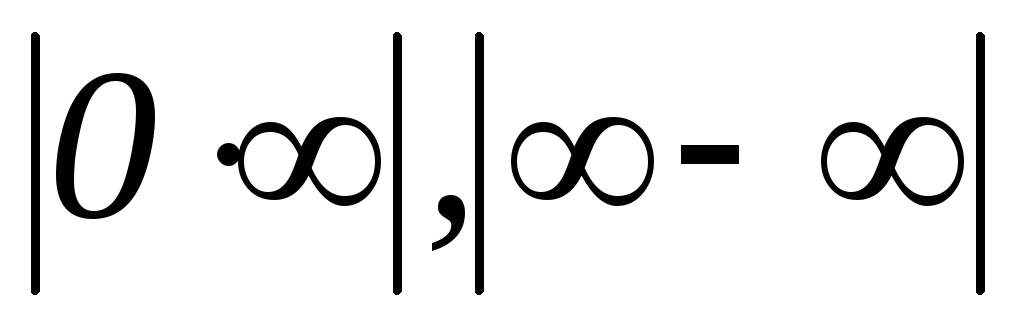с помощью тождественных преобразований приводят к видуи применяют правило Лопиталя.

• Желательно совмещать применение правила Лопиталя с применением эквивалентных бесконечно малых величин. При этом следует строго придерживаться теоремы: заменять эквивалентными можно только в произведении (частном) !

• После каждого применения правила Лопиталя следует проверять, сохранилось ли неопределенное выражение. Если при проверке находятся сомножители, предел которых конечен и не равен нулю (равен числу, отличному от нуля),их сразу заменяют соответствующими пределами.

Примеры

Вычислить пределы по правилу Лопиталя.

	Применять эквивалентные бесконечно малые величины нельзя, т.к. , а не к0.
=	Первое применение правила Лопиталя дает конечный предел.  

	Применять эквивалентные бесконечно малые величины нельзя, выполним тождественные
=	преобразования, чтобы можно было применить правило Лопиталя. Первое применение правила Лопиталя не устраняет неопределенное выражение,
	но проверка пределов сомножителей показывает, что некоторые из них имеют конечные пределы, которыми они и заменяются.
	Еще раз применяется правило Лопиталя.
	Полученный в результате предел бесконечен. 

 - При вычислении пределов сомножителей используются известные величины:

- Раскрытие степенных неопределенных выражений вида

.

Допустим, существует конечный или бесконечный предел степенно-показательной функции (см. раздел о логарифмическом дифференцировании, тема 5). Обозначим его

.

Прологарифмируем данное выражение и применим правило предельного перехода под знаком непрерывной функции (см. раздел о непрерывности функции, тема 4).

		Логарифмируем по основанию е.
		Используем свойства логарифмов (см. приложение) и правило предельного перехода.
	Степень числа е вычисляется как предел.
, где			Окончательно получим формулы, по которым можно вычислять пределы степенно-показательных функций.

 - Часто при вычислении А применяют правило Лопиталя, поэтому полученные формулы для раскрытия степенно-показательной неопределенности иногда называют вторым правилом Лопиталя.

ПРИМЕР

Вычислить предел по второму правилу Лопиталя.

	Допустим нужный предел существует и обозначим его .
	Теперь вычислим показатель степени А. Преобразуем выражение под знаком предела, чтобы можно было применить правило Лопиталя.
	Берем производные от числителя и знаменателя (отдельно!).
		Преобразуем полученное выражение и проверяем неопределенность. Она не устранена.
			Заменяем и снова применяем правило Лопиталя.
			Окончательный ответ. 

Еще примеры вычисления пределов по правилу Лопиталя приведены в разделе "Примеры выполнения обязательных заданий по теме 5".

57