36. Теорема о циркуляции для магнитного поля в веществе

Циркуляция магнитного поля постоянных токов по всякому замкнутому контуру пропорциональна сумме сил токов, пронизывающих контур циркуляции.

Математическая формулировка

В математической формулировке для магнитостатики теорема имеет следующий вид

Здесь  — вектор магнитной индукции,  — плотность тока; интегрирование слева производится по произвольному замкнутому контуру, справа — по произвольной поверхности, натянутой на этот контур. Данная форма носит название интегральной, поскольку в явном виде содержит интегрирование. Теорема может быть также представлена в дифференциальной форме

Эквивалентность интегральной и дифференциальной форм следует из теоремы Стокса.

Приведённая выше форма справедлива для вакуума. В случае применения её в среде (веществе), она будет корректна только в случае, если под j понимать вообще все токи, то есть учитывать и «микроскопические» токи, текущие в веществе, включая «микроскопические» токи, текущие в областях размерами порядка размера молекулы и магнитные моменты микрочастиц.

Поэтому в веществе, если не пренебрегать его магнитными свойствами, часто удобно из полного тока выделить ток намагничения, выразив его через величину намагниченности  и введя вектор напряжённости магнитного поля

Тогда теорема о циркуляции запишется в форме

где под  (в отличие от  в формуле выше) имеются в виду т. н. свободные токи, в которых ток намагничения исключен (что бывает удобно практически, поскольку  — это обычно уже в сущности макроскопические токи, которые не связаны с намагничением вещества и которые в принципе нетрудно непосредственно измерить).

В динамическом случае — то есть в общем случае классической электродинамики — когда поля меняются во времени (а в средах при этом меняется и их поляризация) — и речь тогда идет об обобщенной теореме, включающей  , — всё сказанное выше относится и к микроскопическим токам, связанным с изменениями поляризации диэлектрика. Эта часть токов тогда учитывается в члене  .

Практическое значение

Теорема о циркуляции играет в магнитостатике приблизительно ту же роль, что и теорема Гаусса в электростатике. В частности, при наличии определённой симметрии задачи, она позволяет просто находить величину магнитного поля во всём пространстве по заданным токам. Например, для вычисления магнитного поля от бесконечного прямолинейного проводника с током по закону Био — Савара — Лапласа потребуется вычислить неочевидный интеграл, в то время как теорема о циркуляции (с учётом осевой симметрии задачи) позволяет дать мгновенный ответ:

Если кратко: Циркуляция вектора Н по произвольному замкнутому контуру равна алгебраической сумме токов проводимости, охватываемых этим конутором.

37. Электромагнитная индукция.

38. Ток смещения.

Ток смещения, или абсорбционный ток, — величина, прямо пропорциональная скорости изменения электрической индукции. Это понятие используется в классической электродинамике. Введено Дж. К. Максвеллом при построении теории электромагнитного поля.

Если всякое переменное магнитное поле возбуждает в окружающем пространстве вихревое электрическое поле, то (по Максвеллу), должно существовать и обратное явление: всякое изменение электрического поля должно вызывать появление в окружающем пространстве вихревого магнитного поля.

Для установления количественных соотношений между изменяющимся ЭП и порождаемым им МП Максвелл ввел в рассмотрение ток смещения.

Рассмотрим цепь переменного тока, содержащего конденсатор. Между обкладками заряжающегося и разряжающегося конденсатора существует переменное ЭП. По гипотезе Максвелла через конденсатор “протекают“ токи смещения на тех участках, где отсутствуют проводники.

Переменное ЭП в конденсаторе ( по Максвеллу) в каждый момент времени создает такое МП, как если бы между обкладками существовал бы ток смещения – , равный току в подводящих проводах.

.

(60.1)

По определению

,

(60.2)

где s- поверхностная плотность заряда на обкладках конденсатора. Но мы показывали, что , где D- электрическое смещение в конденсаторе, тогда:

.

(60.3)

С учетом того, что  взаимно параллельны, для общего случая:

.

(60.4)

По определению

,

(60.5)

тогда (60.2) и (60.5) 

.

(60.6)

Следовательно, направление j и j_см., совпадают с направлением вектора .

Выражение (60.6) Максвелл называл плотностью тока смещения.

Подчеркнем, что из всех свойств, присущих току проводимости, Максвелл приписал току смещения лишь одно – способность создавать в окружающем пространстве МП.

В диэлектриках ток смещения состоит из двух слагаемых:

,

(60.7)

где  - напряженность электростатического поля, а - поляризованность, то плотность тока смещения будет равна:

Подставим (60.7) в (60.6), получим:

,

(60.8)

где

(60.9)

плотность тока смещения в вакууме,

(60.10)

плотность тока поляризации, т.е. тока, обусловленного упорядоченным движением электрических зарядов в диэлектрике (смещение зарядов).

Следовательно

.

(60.11)

Название «ток смещения» является условным, по сути это изменяющеесясо временем электрическое поле.

Ток смещения существует не только в вакууме или диэлектрике, но и внутри проводников, по которым проходит переменный ток. Но в проводниках он пренебрежимо мал по сравнению током проводимости.

Максвелл ввел понятие полного тока, равного сумме тока проводимости и тока смещения:

.

(60.12)

Следовательно плотность полного тока равна:

.

(60.13)

Максвелл пришел к тому, что полный ток в цепях переменного тока всегда замкнут, т.е. на концах проводника обрывается лишь ток проводимости, а в диэлектрике (вакууме) между концами проводника существует ток смещения, замыкающий ток проводимости.
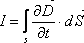