26. Магнитное поле прямого тока

Линии, вдоль которых в магнитном поле располагаются оси маленьких магнитных стрелок, называют магнитными линиями магнитного поля.

Направление, которое указывает северный полюс магнитной стрелки в каждой точке поля, принято за направление магнитной линии магнитного поля.

Цепочки, которые образуют в магнитном поле железные опилки, показывают форму магнитных линий магнитного поля

Если прямой проводник пропустить сквозь лист картона, на который насыпан тонкий слой железных опилок, включить ток и опилки слегка встряхнуть, то под действием магнитного поля тока железные опилки расположатся вокруг проводника не беспорядочно, а по концентрическим окружностям

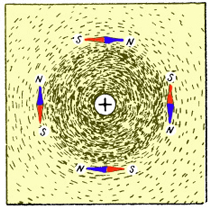
На рисунке показано расположение магнитных стрелок вокруг проводника с током, расположенного перпендикулярно плоскости чертежа, ток в нём направлен от нас, что условно обозначено кружком с крестиком. Оси этих стрелок устанавливаются вдоль магнитных линий магнитного поля прямого тока (рис. а).

При изменении направления тока в проводнике на противоположное (к нам), что условно обозначено кружком с точкой, все магнитные стрелки поворачиваются на 180° (рис. б).

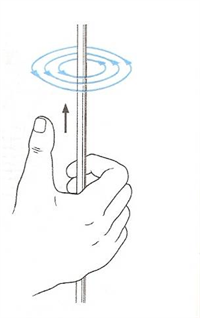
Направление линий магнитного поля можно определить с помощью правила правой руки:

если обхватить проводник с током ладонью правой руки так, чтобы отставленный большой палец был сонаправлен с током, то согнутые четыре пальца укажут направление линий магнитного поля.

27. Магнитное поле кругового тока

Определим магнитную индукцию на оси проводника с током на расстоянии х от плоскости кругового тока. Векторы   перпендикулярны плоскостям, проходящим через соответствующие   и  . Следовательно, они образуют симметричный конический веер. Из соображения симметрии видно, что результирующий вектор   направлен вдоль оси кругового тока. Каждый из векторов   вносит вклад равный , а   взаимно уничтожаются. Но , , а т.к. угол между   и   α – прямой, то   тогда получим

 Подставив   и, проинтегрировав по всему контуру , получим выражение для нахождения магнитной индукции кругового тока:

При , получим магнитную индукцию в центре кругового тока:

 Заметим, что в числителе     – магнитный момент контура. Тогда, на большом расстоянии от контура, при , магнитную индукцию можно рассчитать по формуле:

28. Теорема о циркуляции вектора b

Интеграл вида - циркуляция вектора B→ по замкнутому контуру L.

Циркуляция B равна сумме токов, проходящих через площадь, ограниченную контуром l:

 Вначале рассмотрим случай, когда контур лежит в плоскости перпендикулярно потоку (ток I направлен за чертеж). В каждой точке контура вектор   направлен по касательной к окружности, проходящей через эту точку (линии   прямого тока – окружности).

      Воспользуемся свойствами скалярного произведения векторов.

         где   – проекция dl на вектор  ,  но  , где R – расстояние от прямой тока I до dl.

 .

      Отсюда

 теорема о циркуляции вектора  :  циркуляция вектора магнитной индукции равна току, охваченному контуром, умноженному на магнитную постоянную.

 Итак, циркуляция вектора магнитной индукции   отлична от нуля, если контур охватывает ток.

Такие поля, называются вихревыми или соленоидальными.