21.Основы классической электронной теории электропроводности металлов

 Исходя из представлений о свободных электронах, Друде разработал классическую теорию электропроводности металлов, которая затем была усовершенствована Лоренцем. Друде предположил, что электроны проводимости в металле ведут себя подобно молекулам идеального газа. В промежутках между соударениями они движутся совершено свободно, пробегая в среднем некоторый путь . Правда в отличие от молекул газа , пробег которых определяется соударениями молекул друг с другом, электроны сталкиваются преимущественно не между собой, а с ионами, образующими кристаллическую решетку металла. Эти столкновения приводят к установлению теплового равновесия между электронным газом и кристаллической решеткой. Полагая, что на электронный газ могут быть распространены результаты кинетической теории газов, оценку средней скорости теплового движения электронов можно произвести по формуле . Для комнатной температуры ( 300К) вычисление по этой формуле приводит к следующему значению: . При включении поля на хаотическое тепловое движение, происходящее, со скоростью , накладывается упорядоченное движение электронов с некоторой средней скоростью . Величину этой скорости легко оценить, исходя из формулы, связывающей плотность тока j с числом n носителей в единице объема, их зарядом е и средней скоростью :

Предельная допустимая техническими нормами плотность тока для медных проводов составляет около 10 А/мм2 = 107 А/м2. Взяв для n=1029 м-3, получим Таким образом, даже при больших плотностях тока средняя скорость упорядоченного движения зарядов в 10^8 раз меньше средней скорости теплового движения .

Согласно классической теории средняя длина свободного пробега не зависит от температуры и равна среднему межатомному расстоянию в кристалле. Поэтому, согласно формулe температурная зависимость сопротивления определяется температурной зависимостью скорости теплового движения . Тогда удельное сопротивление согласно классической теории определяется выражением . Однако, экспериментальные данные показывают, что для металлов сопротивление в широком интервале растет линейно с ростом температуры .

основное допущение этой теории – рассмотрение свободных электронов металла как частиц идеального газа, подчиняющихся статистике Максвелла-Больцмана, является неправильным.

22. Закон Ома в дифференциальной форме

Закон Ома в интегральной форме для однородного участка цепи (сила тока на участке, не содержащем ЭДС прямо пропорциональна напряжению)

Для однородного линейного проводника выразим R через ρ:

 

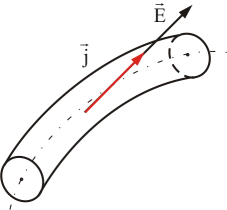
Найдем связь между  и  в бесконечно малом объеме проводника.  В изотропном проводнике (в данном случае с постоянным сопротивлением) носители зарядов движутся в направлении действия силы, т.е. вектор плотности тока  и вектор напряженности поля  коллинеарны.  

Исходя из закона Ома (7.6.1), имеем:

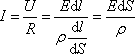
А мы знаем, что  или . Отсюда можно записать

 это запись закона Ома в дифференциальной форме.

Здесь  – удельная электропроводность. Размерность σ – [].