Контрольное задание по курсу "теория вероятностей и

МАТЕМАТИЧЕСКАЯ СТАТИСТИКА", 2007 г., ФУБ

Вариант 4

1. Какова вероятность того, что в январе случайно выбранного года будет четыре воскресенья?

2. Девять водителей гаража в течении дня могут заправляться на 3-х АЗС случайным образом. Найти вероятность того, что на первой заправке заправятся 4 водителя, на второй – два, на третьей – три.

3. В группе из 25 студентов 10 выучили все 30 вопросов для экзамена, 7 - выучили по 20 вопросов, 5 - выучили по 15 вопросов и 3 - по 10. Найти вероятность того, что взятый на удачу студент получит в билете на экзамене три выученных вопроса.

4. В лотерее 20 билетов, из которых 5 выигрышных. Какова вероятность выиграть, имея 4 билета? (Подумайте, что значит выиграть.)

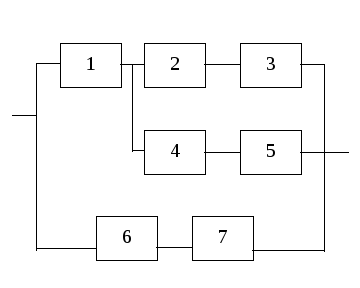
5. Найти вероятность отказа системы элементов, если вероятность работы каждого равна р.

6. В партии из 10 изделий 6 прошло контрольную проверку. На удачу отобрано 3 изделия. Составить закон распределения случайной величины Х- число изделий прошедших контроль среди отобранных и найти ее математическое ожидание, дисперсию.

7. Производится взвешивание некоторого вещества. Случайные ошибки взвешивания подчинены нормальному закону со средним квадратичным отклонением  = 30 г и математическим ожиданием а = 0 г. Оценить вероятность того, что при пятикратном взвешивании хотя бы два раза абсолютная величина ошибки будет менее 20 г.

8. Случайная величина Х распределена равномерно в интервале [10;14]. Проведено 100 измерений, причем удачным считается такое, когда величина Х по абсолютному значению отклонится от математического ожидания меньше, чем на 1. Найти вероятность того, что будет проведено 50 удачных опытов.

9. Для системы, заданной законом распределения, построить безусловные законы распределения составляющих системы и распереление У при Х=6; найти М_х, М_у, D_x, D_y,, r_xy.

Хі \ Yj	10	20	30
2	0.1	0.05	0.1
4	0.15	0.1	0.07
6	0.05	0.1	0.1
8	0.0	0.03	0.15

10. Известны результаты наблюдений: 23, 18, 17, 15, 16, 18, 17, 19, 18, 21, 15, 16, 19, 20, 18, 15, 20, 16, 20, 21, 22, 20, 19, 15, 19, 16, 19, 15, 22, 21, 22, 20, 21, 18, 18, 17, 16, 19, 16, 17, 16, 18, 18, 20, 22, 16, 20, 19, 17, 18, 18, 21, 17, 19, 17, 21, 17, 16, 18, 19,18,21,17,16, 17, 22, 19, 17, 19, 16, 18, 15, 20, 21, 18, 19, 15, 17, 21, 17, 22, 20. Представить результаты наблюдения в виде простого статистического ряда (дискретный вариационный ряд), найти выборочное среднее, выборочную моду, выборочную медиану и выборочную дисперсию. Построить полигон относительных частот. Найти доверительный интервал для оценки математического ожидания и среднего квадратического отклонения наблюдаемой случайной величины с надежностью 0.95.

11. На основе метода наименьших квадратов построить наивероятнейшую статистическую зависимость между переменными, представленными результатами наблюдений:

Хi	-8	-6	-4	-3	-2	-2	1	2
Yi	-3	-2	1	1	2	3	6	6

Построить график кривой и проставить экспериментальные точки.

ЛИТЕРАТУРА:

1. Венцель Е.С. Теория вероятностей. – М., Наука, 1998.

2. Гмурман В.Е. Теория вероятностей и математическая статистика. - М., ВШ, 1998.

3. Гмурман В.Е. Руководство к решению задач по теории вероятностей и математической статистике. – М., ВШ, 1998.

4. Сборник задач по теории вероятностей, математической статистике и теории случайных функций. / Под редакцией А.А. Свешникова. - М., Наука, 1970.

5. Теория вероятностей и математическая статистика. Учебное пособие. / Под редакцией Л.С.Тимченко. – Харьков: НТУ «ХПИ», 1999.