4.5 Расчет позиционного интегрально-дифференцирующего контроллера(pid)

PID – контроллеры, используемые для астатической стабилизации траекторного движения.

Статические системы обладают ошибкой 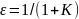,которая зависит от коэффициентов усиления К системы управления.

Астатические системы содержат интегрирующие звенья в передаточной функции W или в передаточной функции цепи обратной связи(ОС).

Рис. Схема системы с позиционно-интегральной дифференцирующей обратной связью(РID- контроллер)

Используется закон управления:

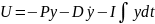
Статическая ошибка системы равна 0

PID- контроллер используется для стабилизации высоты полета лайнера и в системах наведения перехватчиков и управляемых ракет.

Для реализации PID- контроллера требуется измерять координаты на выходе.

На вход системы управления следует подавать разность между значением текущей координаты и ее заданным значением для стабилизации с нулевой ошибкой.

Особенности интеграторов состоят в наличии ошибок выставки и скорости ухода интегратора(накопление ошибки по времени).

Рис. Схема системы управления с тремя вложенными контурами

Решение задачи с использованием системы MATLAB с учетом контура интегрирования координаты по отклонению:

MATLAB :

Margin(r3)→A3

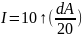
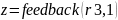
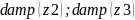
Ltiview

step z2,z3

После выбора коэффициентов усиления для замкнутой системы, с помощью программы damp определяются частоты и коэффициенты демпфирования по формам движения и характеристики переходных процессов для контуров демпфирования, стабилизации и изодромного контура.

5. Синтез корректирующих звеньев в прямой цепи

На пилотажных стендах необходимо обеспечить подобие динамических характеристик базового самолета. В этом случае пилотажный стенд должен обладать такой же полосой пропускания и АФЧХ, как и базовый самолет.

АФЧХ являются желаемыми для настройки пилотажного стенда. В общем случае желаемые АФЧХ определяются показателями:

1. Желаемый коэффициент усиления на малых и средних частотах

2. Свойства минимальной фазовости на малых и средних частотах

3. Статические/ астатические свойства на малых и средних частотах

Изменение АФЧХ реализуется использованием фильтров малых, средних и больших частот

Методика включает использование схемы соединения неизменяемой части системы и фильтра , который является аналоговым или цифровым

Рис. Схема установки корректирующего звена в прямой цепи

W_нч – неизменяемая часть

W_кор – корректирующее устройство

Рис. Логарифмическая амплитудно-частотная характеристика неизменяемой части системы

Рис. Выбор частоты начала коррекции фильтром низких частот

Рис. Выбор частот начала и окончания коррекции фильтром средних частот

Рис. Выбор частот начала и окончания коррекции фильтром высоких частот

Система называется минимально-фазовой , если ее логарифмическая амплитудная частотная характеристика пересекает ось частот под углом

Для минимально-фазовой системы системы можно использовать большие коэффициенты усиления , что обеспечивает большую полосу пропусания.

У неминимально-фазовых систем допустимые коэффициенты усиления ограничены допустимым запасом устойчивости по фазе.

Рис. Запасы устойчивости по фазе для апериодической системы

Колебательное звено:

Рис. Запасы устойчивости по фазе для колебательной системы