4.3 Выбор коэффициентов усиления к в прямой и обратной цепи по заданному запасу устойчивости.

Структура системы управления с коэффициентом усиления в прямой цепи:

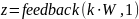
Структура системы управления с коэффициентом усиления в обратной цепи:

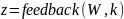
Рис. Схемы систем управления с коэффициентом усиления в прямой и обратной цепи

Рассмотрим замкнутую систему уравнений с неизвестными коэффициентами усиления в прямой/обратной цепи. Требуется найти К по желаемому запасу устойчивости, который может составлять 6;8 или 12дБ

MATLAB : W= tf(…)

margin(W)

A_z = A

φ_z = Б

Рис. Определение запасов устойчивости по логарифмической амплитудно-фазовой характеристике

Увеличение запаса устойчивости приводит к опусканию вниз логарифмической амплитудной характеристики, и полоса пропускания системы опускается.

При уменьшении запаса по амплитуде A_z логарифмическая амплитудная характеристика поднимается вверх, полоса пропускания поднимается, что позволяет эксплуатировать систему в большом диапазоне частот ω.

Рис. Логарифмическая амплитудно-частотная характеристика разомкнутой системы La и логарифмические амплитудные частотные характеристики замкнутой системы отклонению L_y и по ошибке L_ε

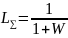
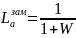
Требуемая

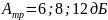
Рекомендуется вычислить значение передаточной функции после коррекции и с использованием программы margin проверить запасы A_z и φ_z.

Ошибки вычисления могут привести к ошибкам выбора коэффициента усиления, которые не создадут требуемого запаса устойчивости по амплитуде и по фазе.

Фазовая характеристика не учитывается при выборе К, поэтому следует проверить наличие запаса устойчивости по фазе φ_z 40 .

4.4 Метод наращивания устойчивых контуров. Выбор коэффициентов усиления позиционно-дифференцирующего и позиционно-интегрально-дифференцирующего контроллера

Позиционный Р- контроллер с жесткой обратной связью:

MATLAB : margin(W)

A_зап = А

dA= A-A_тр

P= 10↑(dA/20)

z= feedback(W,P)

Рис. Схема системы с жесткой обратной связью(Р- контроллер)

Закон управления:

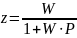
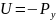
Р-контроллер является жесткой обратной связью и применяется, если исходная разомкнутая система устойчива и не имеет неустойчивых положительных и нулевых вещественных частей корня.

В этом случае жесткая обратная связь позволяет увеличить запас устойчивости до требуемого уровня и обеспечивает нужные значения частоты среза, полосы пропускания и запаса устойчивости по вещественной части корня.

Позиционно-дифференцирующий P-D-контроллер: гибкая обратная связь(ОС)

Структурная схема системы управления с гибкой обратной связью:

Преобразование структурной схемы к системе с двумя контурами:

Рис. Схема системы с гибкой обратной связью(РD- контроллер)

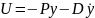
D – контур демпфирования

P-D- контроллер является гибкой ОС по координате и ее производной

Умножая и деля передаточную функцию W в прямой цепи на оператор Лапласа S, получаем двухконтурную систему, включающую внутренний контур и внешний контур стабилизации.

P-D-контроллер используется в системе улучшения устойчивости и управляемости самолета по заданным для пилотирования характеристикам и, включает контуры демпфирования тангажа, крена и рыскания с использованием датчиков угловой скорости. И контуры стабилизации крена , тангажа, нормальной и боковой перегрузок.