4. Частотные критерии анализа устойчивости и синтеза систем уравнения

Частотные критерии используют амплитудно-фазовые частотные характеристики систем уравнения.

Частотные методы включают частотный критерий Михайлова и его приложение для систем управления с единичной отрицательной обратной связью - критерий Найквиста-Михайлова.

4.1 Метод частотного анализа устойчивости Михайлова

Рассматривается передаточная функция системы следующего вида:

X

Y

Характеристическое уравнение Михайлова:

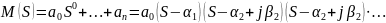
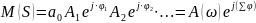
Годограф Михайлова:

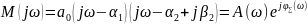
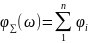
Михайлов предложил рассматривать свойства фазовых частотных характеристик для устойчивых и неустойчивых корней характеристического уравнения.

k - неустойчивость

Рис. Поворот вектора для устойчивой системы и неустойчивого корня

а) Устойчивый вещественный корень

б) Неустойчивый вещественный корень

Для устойчивой системы:

Если система имеет k неустойчивых корней :

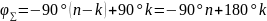
Система устойчива:

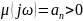
Рис. Годограф Михайлова для устойчивой системы третьего порядка

Критерий устойчивости Михайлова:

Михайлов предложил вычислять значение годографа

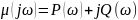
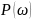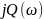- вещественная часть

- мнимая часть

Для значений ω от 0 до достаточно больших величин

Для устойчивости динамической системы необходимо и достаточно выполнение условий:

1. Годограф Михайлова равен свободному члену a_n при частоте ω =0 и должен начинаться на вещественной положительной полуоси

2. При увеличении частоты, движение конца вектора, проведенного из начала координат к годографу, должно проходить против часовой стрелки

3. Угол поворота годографа при увеличении частоты должен быть равен 90 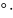n и пересекать n квадрант, где n- степень полинома Михайлова

Система неустойчива:

Рис. Начало годографа на мнимой оси

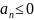
Рис. Годограф Михайлова для неустойчивой системы порядка

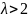
Рис. Годограф Михайлова для неустойчивой системы

Данный метод применим для динамической системы с заданной передаточной функцией. Проблемы в использовании метода связаны с вычислением годографа Михайлова для больших значений ω и большом значении n(8…10)

4.2 Критерий устойчивости Найквиста-Михайлова и запасы устойчивости по амплитуде и по фазе для систем с единичной отрицательной обратной связью

Рассматривается устойчивость замкнутой системы управления с обратной связью. В качестве стандартного формата рассматривается передаточная функция с положительным коэффициентом усиления и единичной отрицательной обратной связью.

Рис. Схемы систем с единичной и неединичной отрицательной обратной связью

Рассмотрим передаточную функцию прямой цепи для устойчивой прямой системы:

,

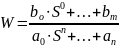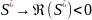
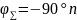
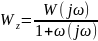
Критическая точка:

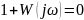
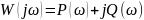
Допускаем ,что замкнутая система с единичной отрицательной обратной связью устойчива. В этом случае S_z^* имеет вещественную часть меньше нуля.

Угол поворота относительно критической точки:

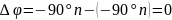
Критерий Найквиста-Михайлова для систем устойчивых в разномкнутом состоянии:

Рис. Годограф Найквиста для устойчивой системы

Если система имеет n устойчивых корней с отрицательной вещественной частью, то будет устойчива и замкнутая система с единичной отрицательной обратной связью если годограф передаточной функции разомкнутой системы не охватывает критическую точку (-1;j₀)

Годограф системы, неустойчивой в замкнутом состоянии:

Рис. Годограф Найквиста для устойчивой системы в разомкнутом состоянии и неустойчивой в замкнутом состоянии

Достоинство данного критерия состоит в том, что об устойчивости замкнутой системы можно судить по годографу разомкнутой системы.

Расположение годографа разомкнутой системы может измениться при отказах автоматики, что приведет к изменению годографа по амплитуде и по фазе.

Запасы устойчивости по амплитуде и по фазе :

По амплитуде показывают на какую величину может увеличиться годограф разомкнутой системы до пересечения критической точки (-1;j₀)

Этот запас равен расстоянию от критической точки разомкнутой системы до годографа вдоль вещественной оси Р

Для системы с резервированием желаемое значение запаса =0,5

Запас по фазе равен угловому расстоянию от P_кр до годографа разомкнутой системы по окружности единичного радиуса

Желаемое значение при запаздывании равном постоянной времени первой формы составляет 60

Пунктирной линией (- - - - -) обозначена единичная окружность

Рис. Годограф с неопределенным запасом устойчивости по фазе системы с амплитудной характеристикой

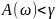
Рис. Определение запасов устойчивости по фазе системы с амплитудной характеристикой

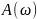
Запасы устойчивости по амплитуде и по фазе в системе MATLAB определяются по логарифмическим амплитудно-фазовым характеристикам.

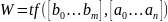
margin(ω)

Запас по амплитуде = 7дБ(ω₁)

Запас по фазе = 47 (ω_β = …)

Рис. Определение запасов устойчивости по амплитуде и по фазе по логарифмическим амплитудно-фазовым характеристикам

Запас устойчивости по амплитуде определяется в точке пересечения фазовой характеристикой уровня - 180

Логарифмическая амплитудная характеристика для устойчивости замкнутой системы должна проходить ниже оси частот и желаемое значение запаса устойчивости по амплитуде состояния 6 Децибел для системы с резервированием и 8-12дБ для систем с трех и четырехкратным резервированием.

Запас устойчивости по фазе определяется в точке пересечения оси частот логарифмической амплитудной характеристикой разомкнутой системы уровня 0.

Запас устойчивости по фазе равен разности частот и уровня 180 . Для резервированной системы желаемое значение составляет 60 .