2.6.4 Анализ характеристик замкнутой системы управления
Модель пространства состояний:
,
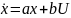
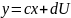где
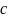– матрица измерений,
– матрица влияния управления.
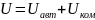
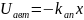
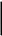
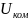
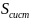x
-
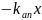
Рис. Схема системы управления
Определяем матрицу динамических коэффициентов замкнутой системы:
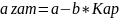
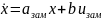
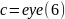
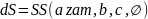
ltivies (step, impulse, bode)
MatLab позволяет скопировать разработанную программу в документ Word и туда же вставить полученные рисунки, опции и копируемые фигуры для отчета о синтезе и анализе результата.
2.7 Аналитическое конструирование оптимального регулятора (акор)
АКОР – представляет собой выбор оптимальных коэффициентов усиления для линейной стационарной системы по квадратичному критерию качества.
В основе метода АКОР лежит применение теоремы Ляпунова об устойчивости для линейных систем, удовлетворяющих условию: положительной определенной квадратичной форме при отрицательном значении ее производной.
Рассматривается линейная система:
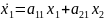
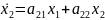
Функция
Ляпунова:
-
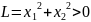
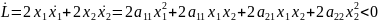
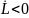система устойчива.
Если
для линейной системы существует
положительно-определенная
– функция Ляпунова и ее производная
,
то линейно-динамическая система
устойчива. Интерпретация метода Ляпунова.
Если функция Ляпунова равна квадрату
расстояния до положения равновесия и
это величина убывает, то система стремится
к положению равновесия, следовательно,
движение к положению равновесия
устойчиво.
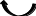
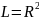
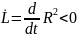
Рис. Интерпретация метода Ляпунова
Пример.
Если
,
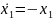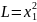
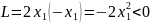– система
устойчива.
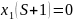, оператор
Лапласа
,
Корень
характеристического уравнения
.
Пример.
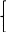
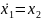
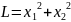
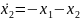
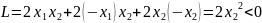– система
устойчива.
Для систем третьего и более высокого порядка сложно подобрать функцию Ляпунова для проверки устойчивости. Для выбора функции Ляпунова на основе метода динамического программирования решена задача о выборе функции Ляпунова методом АКОР.
Для линейной стационарной системы:
…
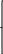
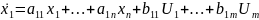
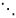
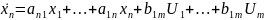
Описываемой векторным уравнением:
Задается квадратичный критерий качества:
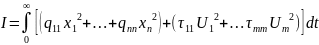
Критерий качества в матричной форме:
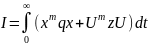
Определяется
оптимально уравнение
из условия минимума квадратичного
критерия. Оптимальным решением является
линейный регулятор
,
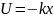где
,
.
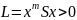Матрица
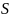определяется из уравнения Риккати:
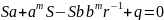
Это уравнение позволяет найти четыре значения для матрицы Сильвестра , из которых два комплексных решения, одно – неустойчивое и только одно устойчивое решение. Это решение определяет оптимальные коэффициенты усиления для задачи аналогичного конструирования.
Для
решения задачи АКОР необходимо ввести
матрицу динамических коэффициентов,
матрицу коэффициентов управления,
матрицы весовых коэффициентов
и
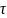и записать обращение к стандартной
программе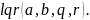
В результате будут вычислены матрицы
оптимальных коэффициентов K,
матрица Сильвестра S
и матрица собственных значений системы
E.
Пример.
I
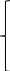
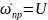
0
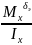0
0
= 1 0 0 0 + 0 U
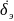0 0 0 1
0
0 0 0 0 1
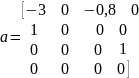
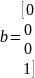
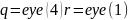
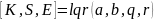
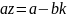
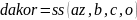
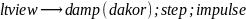
При
выборе весовых коэффициентов
и
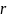можно использовать метод Беллмана:
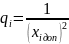
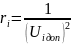
Полученное решение является оптимальным управлением с отрицательной обратной связью по координатам состояния.
Общее число измеряемых координат намного меньше числа координат состояния, поэтому решается задача аналитического конструирования управления только по измеряемым координатам.
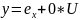
привод
самолет
S
1/S
-
-
Ky
Ky
Рис. Схема управления по измеряемым координатам
MatLab:
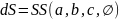
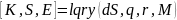
Матрица перекрестных связей:
или
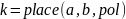
Синтез системы в пространстве состояний основан на описании уравнений движения в математической форме с использованием матрицы динамических коэффициентов а, матрицы управления b, матрицы измерений с и матрицы коэффициентов влияния управления на измерениях d.
Метод размещения измерений матрицы динамических коэффициентов замкнутой системы требует ввода технического задания на значение частот и коэффициентов относительного демпфирования исполнительных устройств, короткопериодического движения самолета и траекторного движения.
Программа place позволяет найти необходимые коэффициенты усиления
.
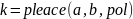Метод АКОР требует задать весовые коэффициенты для квадратов допустимых отклонений координат и управления. В этом случае получается оптимальным по точности система с собственными частотами и коэффициентами демпфирования, которые зависят от выбранных весовых коэффициентов.