
- •Введение
- •Использование преобразование Лапласа для исследования динамических систем
- •Раздел 1. Элементарные звенья систем управления
- •Понятие звена
- •Усилительное звено
- •1.3. Интегрирующее звено
- •1.4. Апериодическое звено
- •1.5. Колебательное звено
- •1.6. Дифференцирующее звено
- •1.7. Звено запаздывания
- •1.8. Частотные характеристики типовых звеньев
- •1.8.1. Частотные характеристики усилительного звена
- •1.8.2. Частотные характеристики интегрирующего звена
- •1.8.3. Частотные характеристики апериодического звена
- •1.8.4. Частотные характеристики колебательного звена
- •1.8.5. Частотные характеристики дифференцирующего звена
- •1.8.6. Частотные характеристики звена запаздывания
- •1.9. Характеристики элементарных звеньев в табличной форме
- •Раздел 2. Линейный анализ и синтез систем управления с использованием математической лаборатории matlab
- •2.1 Анализ и синтез динамической системы в пространстве состояний
- •2.2 Устойчивость систем 1го, 2го порядка и более высокий порядок
- •2.3 Инерционная динамическая система 2-го порядка
- •2.4 Синтез инерционных систем первого и второго порядка
- •2.4.1 Выбор коэффициента усиления в инерционной системе I порядка.
- •2.4.2 Выбор коэффициентов усиления и гибкой обратной связи для инерционной системы второго порядка.
- •2.4.3 Применение методов аналитического синтеза для структуризации систем управления.
- •2.5 Исследование устойчивости для систем порядка n
- •2.5.1 Корневой анализ системы порядка n
- •2.6 Метод синтеза системы управления по желаемому значению частот и коэффициентов относительного демпфирования форм движения изолированной системы
- •2.6.1 Требование к распределению частот и относительных коэффициентов демпфирования изолированных форм движения
- •2.6.2 Выбор коэффициентов усиления по заданным требованиям к собственным значениям, частотам и коэффициентам относительного демпфирования в замкнутой системе
- •2.6.3 Математическая модель в пространстве состояний
- •2.6.4 Анализ характеристик замкнутой системы управления
- •2.7 Аналитическое конструирование оптимального регулятора (акор)
- •3. Алгебраические критерии устойчивости Рауса и Гурвица.
- •4. Частотные критерии анализа устойчивости и синтеза систем уравнения
- •4.1 Метод частотного анализа устойчивости Михайлова
- •4.2 Критерий устойчивости Найквиста-Михайлова и запасы устойчивости по амплитуде и по фазе для систем с единичной отрицательной обратной связью
- •4.3 Выбор коэффициентов усиления к в прямой и обратной цепи по заданному запасу устойчивости.
- •4.4 Метод наращивания устойчивых контуров. Выбор коэффициентов усиления позиционно-дифференцирующего и позиционно-интегрально-дифференцирующего контроллера
- •4.5 Расчет позиционного интегрально-дифференцирующего контроллера(pid)
- •5. Синтез корректирующих звеньев в прямой цепи
- •5.1 Расчет параметров передаточной функции фильтра средних частот (фсч)
- •5.2 Расчет параметров фильтра низких частот (фнч)
- •5.3 Расчет параметров фильтра высоких частот (фвч)
- •6. Синтез корректирующего звена в цепи обратной связи.
- •Процедура улучшения решения за счёт выбора параметров во втором приближении.
- •Раздел 7. Аналитический обзор методов исследования устойчивости систем автоматического управления
- •7.1. Критерии устойчивости [1, 7, 11, 12].
- •7.2. Частотные критерии устойчивости [7, 8, 11].
- •7.3. Запас устойчивости систем [7].
- •7.4. Точность систем [8].
- •7.5. Качество систем [1, 2, 8, 12].
- •7.6. Случайные процессы в системах [8].
- •Литература
2.5 Исследование устойчивости для систем порядка n
Рассматривается линейная стационарная система, движение которой описывается системой n дифференциальных уравнений в форме Коши, разрешенных относительно производных
=
Элементы матрицы динамических коэффициентов А не зависят от времени:
A
=

С использованием программы damp вычисляем собственные значения матрицы динамических коэффициентов А
damp (A)
Собственные значения матрицы динамических коэффициентов А могут быть вещественного либо комплексного типа
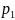 =
=
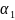
 =
j
=
j
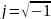
2.5.1 Корневой анализ системы порядка n
Динамическая система имеет n-корней, из которых k – число вещественных корней и n-k – число комплексно сопряженных корней. Если все корни имеют вещественную отрицательную часть, то динамическая система устойчива. Если хотя бы один корень положительный, то система неустойчива.
x
=
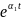 +
+
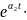 sin(
)
sin(
)
число колебательных форм движения
L
=
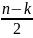
 =
k + L
=
k + L
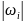 =
=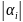 ,
=
,
=
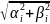
Система
порядка n
имеет
k
апериодических форм движения с частотой
среза
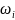 =
=
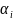 ,
равной модулю вещественной части корня,
и L
=
колебательных форм движения с частотой
среза
,
равной модулю вещественной части корня,
и L
=
колебательных форм движения с частотой
среза
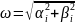
Все формы ранжируются в порядке возрастания частоты от минимальной до максимальной. Главной является 1-я форма с минимальной частотой. Если этой частоте соответствует вещественный корень, то 1-я форма есть апериодическое движение, а если собственное значение – комплексно-сопряженная величина, то 1-я форма представляет собой колебательное движение.


Рис. Варианты первой формы движения апериодического и колебательного типа.
Результатом частотного анализа собственных значений является:
Устойчивость системы, если все вещественные части корней – отрицательны.
Определение 1-ой формы движения по величине минимального по модулю собственного значения частоты (где форма движения может быть апериодической или колебательной в зависимости от того, каким является минимальный по модулю корень (вещественным или комплексно-сопряженным))
Определение числа апериодических форм движения k и колебательных форм движения L
Для каждой формы колебательного движения определяются значения частоты и коэффициента относительного демпфирования.
Для систем с автоматикой требуется, чтобы коэффициент относительного демпфирования составлял
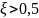 для истребителей,
для истребителей,
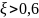 для пассажирских самолетов и не превышал
для пассажирских самолетов и не превышал
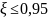 для самолетов всех типов.
для самолетов всех типов.
Пример:
Угловое движение по крену самолета с приводом элеронов.
=
a
+ b
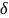
=
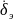 =
=

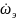 =
-
=
-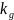 –
–
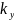
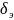 +
+
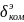 ,
– командный сигнал
,
– командный сигнал


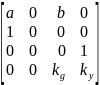
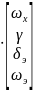 +
+
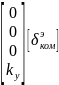
A
=

damp (A)
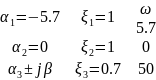
После линейного анализа на устойчивость разомкнутой системы решается задача синтеза системы управления по заданным техническим характеристикам и критериям устойчивости.
2.6 Метод синтеза системы управления по желаемому значению частот и коэффициентов относительного демпфирования форм движения изолированной системы
При исследовании системы из n-дифференциальных уравнений она обладает числами n-вещественных корней и числами l-комплексно-сопряженных корней
n = m + 2l
k = m + l - число форм движения
Для устойчивости замкнутой динамической системы все вещественные части корней должны быть отрицательными, а требования к частотам и коэффициентам относительного демпфирования определяются по заданным техническим требованиям.
Характеристиками
управляемости являются время срабатывания
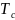 ,
время регулирования
,
время регулирования
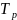 и относительное перерегулирование.
и относительное перерегулирование.
При выборе желаемого коэффициента относительного демпфирования необходимо обеспечить компромисс между быстродействием по времени срабатывания и точностью управления по величине перерегулирования.
Для
приводов выбор коэффициентов обратной
связи по линейному/угловому перемещению
и скорости должен обеспечить коэффициент
относительного демпфирования в диапазоне
0,5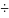 0,7.
0,7.
Для самолетов истребительной авиации минимальное значение коэффициента относительного демпфирования не менее 0,5, а для неманевренных не менее 0,6.
Для
тяжелых самолетов допускается точность
управления с перерегулированием не
более
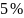 ,
что обеспечивает коэффициент относительного
демпфирования
,
что обеспечивает коэффициент относительного
демпфирования
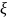 =
=
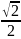 = 0,707.
= 0,707.
На участках точного пилотирования требование к точности отработки командных сигналов достигают 1 2%, что обеспечивает коэффициент относительного демпфирования = 0,95
