2.4.1 Выбор коэффициента усиления в инерционной системе I порядка.

Рассматривается инерционная система первого порядка, передаточная функция которой имеет вид:

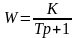или ;

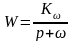где

.

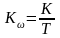Резонансная частота (частота среза при К=1) .

;

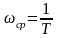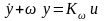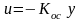
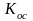
Рис. Схема инерционной системы управления первого порядка с жесткой обратной связью

Рассмотрим уравнение движения системы с обратной связью по отклонению:

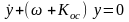
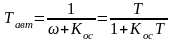
Когда заданы Т и Т_авт , то: , .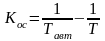

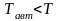Выбор коэффициента усиления жесткой обратной связи для инерционной системы первого порядка выполняется на основании сравнения постоянных времени для исходной системы и желаемого значения.

Для решения задачи выбора демпфера крена следует учитывать ограничения на коэффициент усиления автомата крена (≤ 5).

Пример.

Рис. Схема инерционной системы управления первого порядка, описываемой интегрирующим звеном, с жесткой обратной связью

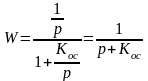
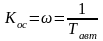
2.4.2 Выбор коэффициентов усиления и гибкой обратной связи для инерционной системы второго порядка.

Рассматривается уравнения движения модели в аэродинамической трубе:

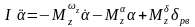
демпфирующий восстанавливающий

момент момент

Для модели в аэродинамической трубе

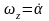
Угол отклонения руля высоты

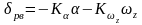
Рис. Схема инерционной системы управления второго порядка с гибкой обратной связью

;

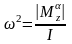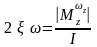
Производные продольного момента вычисляются по формулам:

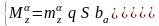
В общем случае движение инерционной системы второго порядка с гибкой обратной связью описывается дифференциальным уравнением:

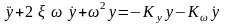
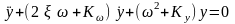
Для настройки автомата устойчивости вычисляет требуемый коэффициент усиления:

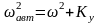
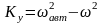
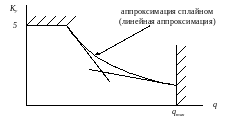
Рис. Зависимость коэффициента усиления автомата устойчивости от скоростного напора

Для автомата демпфирования:

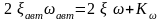
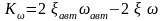
Рис. Зависимость коэффициента усиления автомата демпфирования от скоростного напора

Синтез систем II порядка выполняется на основании желаемых частот и коэффициентов усиления замкнутой системы с гибкой обратной связью и исходной системы.

Выполнение расчетов по скоростному напору q для разных высот Н полета позволяет найти зависимость требуемых коэффициентов от q и аппроксимировать её с использованием линейной интерполяции кусочно-линейной функцией.

Программа настройки автоматов устойчивости и демпфирования ограничена значением q_max (или максимальным значением приборной скорости V_{пр max}) и максимально допустимым коэффициентом усиления.

2.4.3 Применение методов аналитического синтеза для структуризации систем управления.

Структуризация систем управления представляет собой выделение независимых подсистем, которые функционируют самостоятельно на различных режимах. В этом случае систему можно рассматривать как многоконтурную с вложенными контурами. Каждый внутренний контур имеет быстродействие на порядок больше внешнего контура. В этом случае время переходного процесса во внутреннем контуре на порядок меньше времени регулирования во внешнем контуре.

Рис. Переходные процессы в короткопериодическом внутреннем и длиннопериодическом внешнем контурах структуризованной системы

На современных самолетах используются режимы автоматического, полуавтоматического и ручного управления.

Рассмотрим электрический привод, описываемый уравнением:

, где 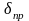– угол поворота вала привода.

Закон управления приводом:

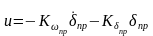
Собственное возмущенное движение привода с гибкой обратной связью описывается уравнением:

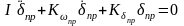
В этом случае привод с гибкой обратной связью обладает собственной частотой и коэффициентом относительного демпфирования:

;

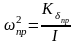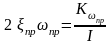
Обычно выбирают ;

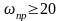Для управления короткопериодическим угловым движением самолета используется соотношение между желаемой частотой привода и частотой короткопериодического углового движения самолета с автоматикой 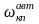в соответствии с неравенством:

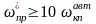
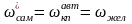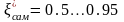; (2 контур)

Для траекторного контура желаемая частота длиннопериодического колебательного движения выбирается на один – два порядка меньше частоты короткопериодического углового движения самолета

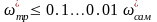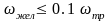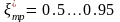; ; (3 контур)

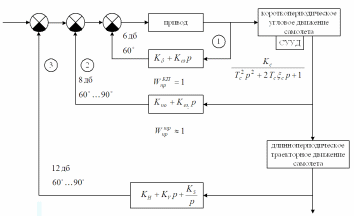
Рис. Схема системы управления самолета с вложенными контурами управления следящим электрическим приводом, системой улучшения устойчивости и управляемости углового движения и астатической системы стабилизации высоты

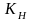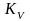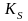При синтезе траекторного контура передаточной функции привода и самолета в угловом движении считаются идеальными. Выполняется расчет управляющего устройства (контролера), который включает в закон управления позиционный сигнал по высоте , коэффициент усиления по скорости набора высоты v_y и изодромный интегральный сигнал от ошибки регулирования высоты с коэффициентом усиления , позволяющий создать астатизм и обеспечить нулевую среднюю ошибку стабилизации.