
EMM_dlya_EKZ-31_51 / Лекции_ЭММ / Теми_9,10
.pdf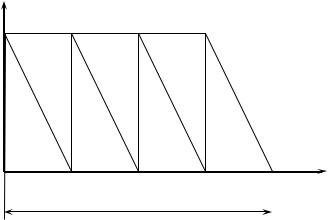
ТЕМА 9. СТАТИЧНА ДЕТЕРМІНОВАНА БЕЗДЕФІЦИТНА ЗАДАЧА УПРАВЛІННЯ ЗАПАСАМИ
9.1. Оптимізація запасу продукту одного виду
Задачі управління запасами складають один із великих розділів економічних задач дослідження операцій. Правильне та своєчасне визначення оптимальної стратегії управління запасами, а також оптимального рівня запасів дозволяє звільнити значні обігові кошти, заморожені у вигляді запасів при одночасному забезпеченні безперебійного функціонування підприємств виробничої сфери чи сфери обслуговування.
Введемо поняття інтенсивності витрати запасу b(t), яку також називають попитом на продукт, що запасається. В залежності від того b(t) приймається детермінованою чи вірогіднісною моделі управління запасами поділяють на детерміновані та стохастичні. В рамках даного розділу розглянемо детерміновану модель управління запасами. В статичній детермінованій бездефіцитній моделі управління запасами (яку в іноземній літературі називають класичною задачею економічного розміру замовлення [1]) приймаються наступні припущення:
-однаковий розмір n кожного із замовлень;
-недопустимість дефіциту на продукт, що запасається;
-миттєве поповнення запасу.
Загальне споживання продукту за певний час τ позначимо, через N. Припустимо, що інтенсивність витрат запасу визначається залежністю:
b = |
N . |
(9.1) |
|
τ |
|
Поповнення замовлення здійснюється миттєво партіями однакового розміру n , тому функція постачання a(t) не є безперервною: a(t) = 0 при усіх t , окрім моментів постачання продукту, коли a(t) = n . Так як інтенсивність витрат запасу постійна b = const , то уся партія буде використовуватись за період часу:
T = n . |
(9.2) |
b |
|
Графік залежності кількості запасів від часу показаний на рис. 9.1, при побудові якого за початок відліку брався момент постачання першої партії. Для зручності загальний час τ приймаємо кратним періоду T.
n
b |
b |
b |
b |
0 |
T |
|
2T |
|
|
3T |
|
4T |
t |
|
|
τ |
|
|
|
||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||
|
|
|
|
|
|
|
|
|
|
Рисунок 9.1 – Графік залежності кількості запасів від часу
Кількість партій необхідних для забезпечення потреб протягом періоду часу τ дорівнює:
k = |
N |
= |
τ |
. |
(9.3) |
n |
|
||||
|
|
T |
|
||
Таким чином наша задача управління запасами полягає у визначенні такого об’єму партії n , при котрому сумарні витрати C на створення Cст. та
зберігання Cзб. запасів були б мінімальними:
С(n) =Сст. (n) +Сзб. (n) → min. |
(9.4) |
Очевидно, що тут у якості критерію оптимальності будуть виступати витрати на створення та зберігання запасу, які мінімізуються. У якості КЗ буде виступати об’єм партії n.
Витрати на створення запасу однієї партії продукту позначимо через сст. , тоді загальні витрати на створення запасів протягом часу τ:
Cст. (n) = сст. k = cст. |
N |
= cст. |
τ |
. |
(9.5) |
n |
|
||||
|
|
T |
|
||
Під витратами сст. на створення запасу продукту розуміють витрати на
завантаження-розвантаження транспортних засобів, транспортування продукту, оформлення необхідних паперів, наприклад митних.

Витрати на зберігання одиниці продукції позначимо через сзб.. Середній запас за проміжок часу [0;T ] дорівнює n2T . Таким чином витрати на
зберігання усього запасу при лінійній по часу його витраті дорівнюють витратам на зберігання середнього запасу:
Сзб. (n) = сзб. |
n T |
k = сзб. |
n T |
|
N |
= cзб. |
T N |
= cзб. |
n τ |
. |
(9.6) |
|
|
n |
|
|
|||||||
2 |
2 |
|
2 |
2 |
|
|
|||||
Враховуючі залежності (9.5) та (9.6) сумарні затрати (9.4) визначаються залежністю, яка є ЦФ детермінованої бездефіцитної задачі управління запасами:
С(n) = cст. |
N |
+cзб. |
n τ |
→ min . |
(9.7) |
n |
|
||||
|
2 |
|
|
||
Графіки функції витрат на створення та зберігання запасів, а також загальних витрат представлені на рис. 10.2.
Рисунок 10.2 – Графік функції витрат на створення та зберігання запасів
Як видно із рис. 9.2 залежність сумарних витрат від об’єму партії n є унімодальною функцією, причому її мінімум досягається при
′ |
cст. N |
|
cзб. |
τ |
|
|
C (n) = − |
|
+ |
|
|
=0 |
(9.8) |
n2 |
2 |
|
Із (9.8) отримаємо:
nopt = |
2 |
cст. N |
. |
(9.9) |
|
cзб. τ |
|||
|
|
|
|
Враховуючі (9.1) формулу (9.9) можна переписати у вигляді
nopt = |
2 |
cст. b |
. |
(9.10) |
|
cзб. |
|||
|
|
|
|
Залежність (9.10) отримала назву формули Уілсона, який запропонував її у 1927 році. Отримання формули (9.10) було здійснено класичними методами диференціального числення. ЦФ є унімодальною із явно вираженим мінімумом, тобто вона допускає безумовну оптимізацію.
9.2. Узагальнення класичної детермінованої бездефіцитної задачі на випадок умовної оптимізації кількості запасів декількох видів продуктів
Припустимо, що перед нами стоїть задача мінімізації витрат на створення та зберігання не одного, а декількох видів продуктів j =1...m. В такому
випадку у нас буде m КЗ (n1 ,..., nm ), економічним сенсом яких будуть кількості продуків, що запасаються. Тоді ЦФ (9.7) можна записати у вигляді:
|
|
|
|
m |
|
|
|
Ni |
|
|
|
ni τ |
|
|
|
С(n |
,...,n |
m |
) = |
|
c |
ст.i |
|
+c |
зб.i |
|
|
→ min . |
(9.11) |
||
|
|
|
|||||||||||||
1 |
|
|
∑ |
|
ni |
2 |
|
|
|
||||||
|
|
|
|
i=1 |
|
|
|
|
|
|
|
||||
Функція (9.11) є адитивною, тобто оптимізацію можна проводити по кожній КЗ ni окремо за формулою Уілсона (9.10).
Адитивність – властивість величини, яка полягає у тому, що значення цієї величини, яке відповідає цілому об'єкту, дорівнює сумі значень величин, що відповідають його частинам. Найбільш простим прикладом адитивної величини в економіці є гроші.
В процесі створення та зберігання запасів можуть виникати певні обмеження на значення КЗ – розмірів запасів кожного із продуктів.
При запасанні продукту необхідні не тільки витрати на його створення та зберігання, але і на його придбання. Очевидно, що запаси заморожують обігові кошти, тому бюджет на покупку продуктів в запас B може бути обмежений:
m |
|
∑cод.i ni ≤ B |
(9.12) |
i=1
де cод.i – ціна одиниці продукту, що запасається.
Загальна кількість запасу займає певний об’єм складу, який також може бути обмежений:
m |
|
∑vi ni ≤W |
(9.13) |
i=1
де vi – об’єм, що займає одиниця продукції на складі; W – корисний об’єм складу.
Обмеження можуть бути пов’язані із мінімально необхідною кількістю певного виду запасу Mi . , яка може бути більшою ніж оптимальне його значення отримане за формулою Уілсона ni ≥ Mi.
Також транспортування замовленої продукції може здійснюватись декількома транспортними засобами, які доцільно завантажувати повністю. Це може призвести до необхідності накладення обмежень дискретності на об’єми закупівель продукції в запас.
Накладання обмежень на значення ni . скоріше за все призведе до погіршення результату порівняно із оптимізацією за формулою Уілсона. Також необхідно відмітити, що умовну оптимізацію розмірів запасів доцільно проводити градієнтними методами або методом множників Лагранжу, оскільки при наявності обмежень оптимальні рішення можуть лежати не в стаціонарній точці функції (9.11), а на границі її області визначення.
Список використаної літератури
1.Таха, Хемди А. Введение в исследование операций / Таха, А. Хемди, 7-е изд.; пер. с англ. – М.: Издательский дом "Вильяме", 2005. – 912 с.
2.Исследование операций в экономике : учеб. пособие для вузов / Н.Ш. Кремер, Б.А. Путко, И.М. Тришин, М.Н. Фридман; под ред. проф. Н.Ш Кремера. – М.: ЮНИТИ, 2002. – 407 с.
3.Кузьмичов А.І., Медведєв М.Г. Математичне програмування в Excel: Навч. посіб. – К. Вид-во Європ. Ун-ту, 2005. – 320 с.
4.Скворчевський О.Є., Попенко А.О., Неупокоєва А.О. Особливості оптимізації запасів підприємства засобами MathCAD за формулою Уілсона при додаткових обмеженнях // Моделювання та прогнозування економічних процесів: Матеріали ІV Міжнародної науково-практичної конференції. – К.:
НТУУ «КПІ», 2010. – С. 46-47.
ТЕМА 10. ДИНАМІЧНЕ ПРОГРАМУВАННЯ
10.1. Сутність динамічного програмування
В економіці та менеджменті зустрічаються задачі у яких процес прийняття управлінських рішень носить багатокрокову структуру наприклад оптимальне по деякому критерію розподілення капіталовкладень у підприємство чи декілька пов’язаних підприємств протягом декількох років, задачі планування діяльності економічного об’єкта (підприємства, галузі, тощо) із урахуванням змін у часі потреб у продукції, що виробляється. Хоча слово «динамічне» вказує на присутність фактора часу (причому час, як правило, приймається дискретним) у задачах, тим не менш динамічне програмування може бути застосовано і до «статичних» задач, як наприклад деякі задачі розподілення ресурсів.
Основи динамічного програмування були запропоновані американським математиком Річардом Белманом у 40-50-х роках ХХ ст.
Динамічне програмування – розділ прикладної математики, що розробляє теорію та методи знаходження оптимальних по деякому критерію багатокрокових керуючих впливів.
10.2 Постановка задачі динамічного програмування
Для вирішення задачі динамічного програмування використовуються наступні позначення:
N – число кроків;
xk =(x1k , x2k ,...., xnk ) – вектор, що описує стан системи на k-му кроці; x0 – початковий стан на першому кроці;
xN – кінцевий стан на останньому N-му кроці; Хk – область допустимих станів на k-му кроці;
uk = (u1k ,u2k ,...,umk ) – вектор керуючих впливів на k-му кроці, що забезпечує перехід системи із стану xk −1 у стан xk ;
Uk – область допустимих керуючих впливів на k-му кроці;
Wk – величина виграшу, отриманого у результаті реалізації k-го кроку; S – загальний виграш за N кроків;
u * = (u1* , u2* ,..., uN* ) – матриця оптимальної стратегії керування або оптимальний керуючий вплив за N кроків.
Sk +1 (xk ) – максимальний виграш, отриманий при переході із будь-якого стану xk у кінцевий стан xN при оптимальній стратегії керування починаючи із (k +1) -го кроку.
S1 (x0 ) – максимальний виграш, отриманий за N кроків при переході системи із початкового стану x0 у кінцевий стан xN при реалізації оптимальної стратегії
© Скворчевський О.Є., 2012 |
керування u * . |
|
Метод динамічного програмування спирається на умову відсутності наслідків та |
|
умову адитивності цільової функції. |

Умова відсутності наслідків полягає у тому, що стан xk , у котрий перейшла система за один k-й крок, залежить від попереднього стану системи xk −1 і вибраного керуючого впливу uk , але не залежить від того, яким чином система перейшла із стану xk −1 у стан xk , тобто:
xk = fk (xk −1,uk ). |
(10.1) |
Рівняння (10.1) часто називають рівнянням стану системи.
Аналогічно величина виграшу Wk залежить від попереднього стану системи xk −1 і вибраного керуючого впливу uk , тобто:
Wk = zk (xk −1,uk ). |
(10.2) |
Величину виграшу Wk також називають цільовою функцією k-го кроку.
Умова адитивності цільової функції задачі полягає у тому, що загальний виграш S за N кроків розраховується за формулою:
|
N |
N |
,uk ) . |
|
S = |
∑Wk |
= ∑zk (xk −1 |
(10.3) |
|
|
k =1 |
k =1 |
|
|
Оптимальною стратегією керування u * називається сукупність керуючих впливів u1* , u2* ,..., uN* у результаті реалізації яких система за N кроків переходить із початкового стану x0 у кінцевий стан xk і при цьому загальний виграш S приймає найбільше значення.
Примітка 1: адитивність – властивість величини, яка полягає у тому, що значення цієї величини, яке відповідає цілому об'єкту, дорівнює сумі значень величин, що відповідають його частинам. Найбільш простим прикладом адитивної величини в економіці є гроші.
Траєкторія системи – послідовність станів x1, x2 ,...., xN .
Умова відсутності наслідків дозволяє сформулювати принцип оптимальності Белмана.
Принцип оптимальності Белмана полягає у тому, що яким би не був допустимий стан системи xk −1 Хk −1 перед черговим і-м кроком, потрібно обирати такий
допустимий керуючий вплив uk Uk на цьому кроці так, щоб виграш Wk на k-му кроці плюс виграш на усіх наступних кроках був максимальним:
Sk (xk −1 ) = max{Wk +Sk +1(xk )}. |
(10.4) |
uk |
|
Sk (xk −1 ) = max{zk (xk −1,uk ) + Sk +1(xk )}. |
(10.4´) |
uk |
|
Рівняння (10.4) отримало назву основного рекурентного співвідношення Белмана,
також його називають основним функціональним рівнянням динамічного програмування.
Обчислення в динамічному програмуванні виконуються рекурентно в тому сенсі, що вихідна задача розбивається на декілька більш простих підзадач. Потім оптимальне рішення однієї підзадачі використовується у якості вихідних даних для наступної підзадачі. Вирішивши останню підзадачу, ми отримуємо оптимальне рішення вихідної задачі [1].
Примітка 2: Рекурентним співвідношенням називають співвідношення за допомогою яких нові значення змінних знаходять через попередні значення цих та інших змінних знайдених на одній чи декількох попередніх ітераціях. Система рекурентних співвідношень має бути повною, тобто вказувати процедури обчислення усіх змінних за допомогою лише їх попередніх значень, даних задачі та констант. Рекурентні співвідношення можуть визначати умови формування скалярних величин, векторів, матриць, а також будь яких математичних об’єктів, наприклад множин [3].
Важливо відмітити, що максимальний виграш отриманий при переході із передостаннього xN −1 у кінцевий стан xN буде визначатися залежністю:
SN (xN −1 ) = max{zN (xN −1,uN )}. |
(10.5) |
uN |
|
Рівняння (9.5) означає, що керуючий вплив uN на останньому кроці визначається
лише за максимальним виграшем на цьому кроці.
Оптимально спланував останній крок N можна перейти до оптимального планування передостаннього N −1 кроку, потім до кроку N −2 і т.д., поки не буде знайдена величина S1 (x0 ) максимального виграшу, отриманого за N кроків при
переході системи із початкового стану x0 у кінцевий стан xN при реалізації
оптимальної стратегії керування u * . Тому на першому етапі процес динамічного програмування розгортається від кінця до початку.
Однак для визначення максимального виграшу на останньому кроці необхідно знати вектор стану системи на ( N −1)-му кроці xN −1 , який на першому етапі рішення нам не відомий. Очевидно, що потрібно розглянути усю область допустимих станів ХN −1 на ( N −1)-му кроці та визначити такий стан при якому виграш на N -му кроці буде максимальним. Таким чином вибір оптимального керуючого впливу uN буде
залежати від x . Величина u * (x − )
N −1 N N 1
керуючого впливу на N -му кроці.
Визначивши uN* (xN −1 ) можна перейти до
u * − (x − ) за залежністю:
N 1 N 2
отримала назву умовно оптимального
( N −1 )-го кроку на якому визначити
SN* −1 |
(xN −2 ) = max{z*N −1(xN −2 ,uN* |
−1 ) +uN* |
(xN −1 )}. |
|
* |
|
|
|
uN −1 |
|
|
У загальному випадку умовно оптимальний керуючий вплив u * (x − )
k k 1
визначається за залежністю:
S* (x − ) = max{z* (x − , u * ) + S*+ (x )}.
k k 1 uk* k k 1 k k 1 k
Таким чином у результаті першого етапу рішення задачі програмування отримують дві послідовності функцій:
1. |
Умовні екстремуми (максимуми) Sk* (xk −1) ; |
2. |
Умовно оптимальні керуючі впливи uk* (xk −1 ) . |
(10.6)
на k-му кроці
(10.7)
динамічного
Зазначені функції у безперервних моделях отримують аналітично, а дискретних задачах (більшість задач динамічного програмування) – у табличній формі.
Після виконання першого етапу – визначення умовно оптимальних по заданому критерію керуючих впливів переходять до другого етапу – визначенню безумовно оптимальних керуючих впливів.
При визначеному початковому стані x0 на першому кроці визначають максимальний виграш S1(x0 ) :
S1(x0 ) = max{z1(x0 , u1 ) + S2 (x1 )}. |
(10.8) |
u1 |
|
Потім безумовний оптимальний керуючий вплив по ланці: |
|
x0 → u1 → x1 → u2 →... → xN −1 → uN → xN . |
(10.9) |
Таким чином із двох етапів рішення задач динамічного програмування найбільш важливим та трудомістким є перший етап. На другому етапі фактично залишається лише визначити вектор оптимальної стратегії керування за N кроків
u * = (u1* , u2* ,..., uN* ) по прорахованих на першому етапі варіантів.
9.3. Загальна схема застосування методу динамічного програмування
Побудова моделі та застосування методу динамічного програмування для рішення задачі може бути розділено на наступні етапи [2]:
1.Обрання способу ділення процесу управління на кроки.
2.Обрання параметрів вектору x(k −1) = (x1(k −1) , x2(k −1) ,...., xn(k −1) ) , що описує стан
системи на k-ум кроці, а також вектору uk = (u1k ,u2k ,...,umk ) керуючих впливів на k- му кроці.
3.Записують рівняння стану (9.1) для конкретної задачі виходячи із її економічного сенсу.
4.Вводять цільові функції k-го кроку (функції виграшів на k-му кроці) та сумарну цільову функцію задачі.
5. |
Вводять умовний екстремум Sk* (xk −1 ) та умовно оптимальний керуючий |
|
вплив uk* (xk −1 ) на k-му кроці. |
|
|
6. |
Записують рівняння Белмана для останнього |
SN* (xN −1 ) та інших Sk* (xk −1 ) |
кроків. |
|
|
7. |
Послідовно вирішують рівняння Белмана (умовна оптимізація) та отримують |
|
дві послідовності функцій: Sk* (xk −1 ) та uk* (xk −1 ) . |
|
|
8. |
Після виконання умовної оптимізації отримують оптимальне рішення для |
|
конкретного початкового стану x0 Smax = S1* ( x0 ) |
та далі по ланцюжку (10.9) |
|
матрицю оптимальної стратегії керування.
Окрім розглянутого вище методу «зворотної прогонки», також існує метод «прямої прогонки» [1].
10.4. Задача оптимального розподілення інвестицій між підприємствами протягом N років [2].
Задача. Інвестиційний фонд планує вкласти кошти в загальному обсязі х0 =10000 у.о. в два підприємства на 4 роки. Кошти u вкладені у 1-е підприємство на початку року, дають у кінці року прибуток у розмірі f1 (u) = 0,6 u та повертаються у розмірі
q1 (u) = 0,7 u ; |
аналогічно |
для 2-го підприємства функція прибутку дорівнює |
f2 (u) = 0,5 u , |
а функція |
повернення коштів q2 (u) = 0,8 u. В кінці року усі |
повернені кошти заново перерозподіляються між 1-м та 2-м підприємством, нові кошти не надходять, а отриманий прибуток у виробництво не вкладається. Потрібно розподілити кошти х0 =10000 у.о. між двома підприємствами на 4 роки таким чином, щоб сумарний прибуток від обох підприємств протягом 4-х років був максимальним.
Рішення.
1.Процес розподілення коштів між двома підприємствами розгортається в часі протягом 4-х років. Управлінські рішення приймаються на початку кожного року. Відповідно кількість кроків буде 4, а їх номер буде співпадати із номером року на який приймається рішення про розподілення коштів між двома підприємствами.
2.Керована система – два підприємства, а процес керування полягає розподіленні коштів між підприємствами у кожному з років. В даному випадку стан системи характеризує не вектор, а лише одна скалярна величина x(k −1) – кількість
коштів, що підлягають розподілу між підприємствами на початку k-го року.
На перший погляд вектор керуючих впливів на k-му кроці складається із двох елементів:
uk = (u1k , u2k ) . |
(10.10) |
де u1k – кількість коштів виділених 1-му підприємству на початку k-го року; u2k – кількість коштів виділених 2-му підприємству на початку k-го року.
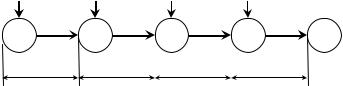
Однак усі кошти x(k −1) підлягають розподіленню між двома підприємствами, тому u2k = x(k −1) −u1k . Тоді керуючий вплив на k-му кроці потрібно характеризувати не вектором (9.10), а скалярною величиною u1k , яку далі будемо називати просто uk .
u1 |
u2 |
|
u3 |
|
u4 |
|
х1 |
х2 |
|
х3 |
|
х4 |
х5 |
|
|
|||||
1-й крок |
2-й крок |
|
3-й крок |
|
4-й крок |
|
|
|
|
|
|
|
|
Рис. 10.1. – Схема процесу керування системою із 2-х підприємств протягом 4-х років
3. |
Рівняння стану системи в даному випадку матиме вигляд: |
|
|
xk = q1(uk ) +q2 (x(k −1) −uk ) |
(10.11) |
або |
|
|
|
xk = 0,7 uk +0,8 (x(k −1) −uk ) = 0,8 x(k −1) −0,1 uk . |
(10.11´) |
Рівняння характеризує повернення коштів наприкінці k-го кроку. |
|
|
4. |
Цільова функція k-го кроку матиме вигляд: |
|
|
Wk = f1 (uk ) + f2 ( x(k −1) −uk ) |
(10.12) |
або |
|
|
|
Wk = 0,6 uk +0,5 ( x(k −1) −uk ) = 0,1 uk +0,5 x(k −1) . |
(10.12´) |
Тоді, виходячи із умови адитивності, сумарну цільову функцію задачі можна записати у вигляді:
|
4 |
4 |
uk +0,5 |
x(k −1) ) . |
|
S = |
∑Wk |
= ∑(0,1 |
(10.13) |
||
|
k =1 |
k =1 |
|
|
|
Економічним сенсом цільової функції (9.13) буде сумарний прибуток за 4 роки.
5. Нехай S* (x − ) умовно оптимальний прибуток за (N −(k +1)) років,
k (k 1)
починаючи із k-го року включно, при умові, що наявні на початок k-го року кошти x(k −1) в подальшому будуть розподілені оптимально.
6. Рекурентні співвідношення Белмана почнемо записувати із останнього кроку, тобто для 4-го року:
|
|
S4 (x3 ) = max(0,1 u4 +0,5 x3 ). |
(10.14) |
Для 3-го кроку: |
|
u4 |
|
|
|
|
|
S3 (x2 ) = max[(0,1 u3 +0,5 x2 ) + S4 (x3 )]. |
(10.15) |
||
|
|
u3 |
|
Для 2-го кроку: |
|
|
|
S2 |
(x1 ) = max[(0,1 u2 +0,5 x1 ) + S3 (x2 )]. |
(10.16) |
|
|
|
u2 |
|
Для 1-го кроку: |
|
|
|
S1 |
(x0 ) = max[(0,1 u1 +0,5 x0 ) + S2 (x1 )]. |
(10.17) |
|
|
|
u1 |
|
7. Проведемо умовну оптимізацію послідовно вирішивши рівняння Белмана починаючі із останнього 4-го кроку. Враховуючі, що 0 ≤ u4 ≤ x3 максимальне
значення рівняння (10.14) може бути досягнуто при u4 = x3. Тоді рівняння (10.14) матиме вигляд:
S4 (x3 ) = 0,6 x3. |
(10.18) |
Враховуючі формулу (10.18) рекурентне співвідношення Белмана (10.15) для 3-го кроку можна переписати у вигляді:
|
S3 (x2 ) = max[(0,1 u3 +0,5 x2 ) +0,6 x3 ]. |
(10.19) |
|
u3 |
|
Рівняння (10.11′) стану системи на початку 4-го кроку: |
|
|
|
x3 = 0,8 x2 −0,1 u3. |
(10.20) |
Тоді співвідношення (10.19) перепишемо у вигляді: |
|
|
S3 |
(x2 ) = max[0,1 u3 +0,5 x2 +0,6 (0,8 x2 −0,1 u3 )]. |
(10.21) |
|
u3 |
|
S3(x2 ) = max[0,98 x2 +0,04 u3 ]. |
(10.21′) |
|
|
u3 |
|
Область допустимих значень |
u3 має вигляд 0 ≤ u3 ≤ x2 , тоді (10.21′) |
прийме |
найбільше значення при u3 = x2 |
: |
|
|
S3 (x2 ) =1,02 x2 |
(10.22) |
Підставивши (10.22) в (10.16) отримаємо рекурентне рівняння Белмана для 2-го кроку:
|
S2 (x1 ) = max[0,1 u2 +0,5 x1 +1,02 x2 ]. |
(10.23) |
|
u2 |
|
Рівняння (10.11′) стану системи на початку 3-го кроку: |
|
|
|
x2 = 0,8 x1 −0,1 u2 . |
(10.24) |
Тоді |
(x1 ) = max[0,1 u2 +0,5 x1 +1,02 (0,8 x1 −0,1 u2 )]. |
|
S2 |
(10.25) |
|
|
u2 |
|
|
S2 (x1 ) = max[1,316 x1 −0,002 u2 ]. |
(10.25′) |
|
u2 |
|
Враховуючі те, що u2 |
може змінюватись в межах 0 ≤ u2 ≤ x1, максимальне значення |
|
(10.25′) буде досягатися при u2 = 0, тобто |
|
|
|
S2 (x1 ) =1,316 x1. |
(10.26) |
Аналогічно попереднім розрахункам рекурентне рівняння Белмана для 1-го кроку можна представити у вигляді:
S1 (x0 ) = max[(0,1 u1 +0,5 x0 ) +1,316 x1 ]. |
(10.27) |
u1 |
|
Рівняння стану на початку 2-го кроку: |
|
x1 = 0,8 x0 −0,1 u1. |
(10.28) |
Тоді (10.27) матиме вигляд: |
|
S1 |
(x0 ) = max[(0,1 u1 +0,5 x0 ) +1,316 (0,8 x0 −0,1 u1 )]. |
(10.27) |
|
u1 |
|
|
S1 (x0 ) = max[1,5528 x0 −0,0316 u1 ]. |
(10.27′) |
|
u1 |
|
Враховуючі те, що u1 може змінюватись в межах 0 ≤ u1 ≤ x0 , максимальне значення (10.25′) буде досягатися при u1 = 0, тобто
S1 ( x0 ) =1,5528 x0 . |
(10.28) |
На цьому етапі умовна оптимізація закінчується.
8. Максимальний прибуток, отриманий від двох підприємств за 4 роки при початково вкладених коштах у розмірі 10000 у.о., буде складати 15528 у.о. При умові, що розподілення коштів по роках буде таким, як наведено в табл. 9.1.
Таблиця 10.1. Оптимальне розподілення коштів між двома підприємствами, протягом 4-х років
Підприємство |
|
|
Рік (крок) |
|
|
1 |
2 |
|
3 |
4 |
|
|
|
||||
1 |
0 |
0 |
|
6400 |
4480 |
2 |
10000 |
8000 |
|
0 |
0 |
Таблиця 10.1 є матрицею оптимальної стратегії керування. Для більш складних задач ніж розглянута таку матрицю доцільно будувати за допомогою комп’ютера.
Використана література:
1.Таха Хемди А. Введение в исследование операций, 7-е издание.: Пер. с англ. – М.: Издательский дом «Вильямс», 2005. – 219 с.
2.Исследование операций в экономике: Учеб. пособие для вузов /Н.Ш. Кремер, Б. А. Путко, И.М. Тришин, М.Н. Фридман; Под ред. проф. Н.Ш. Кремера. – М:
ЮНИТИ, 2002. – 407 с.
3.Математика и кибернетика в экономике. Словарь-справочник. Изд. 2-е, перераб. и доп. М., «Экономика», 1975. – 700 с.
4.Беллман Р. Динамическое программирование. Перевод с англ. – М.: Издательство иностранной литературы, 1960. – 401 с.
5.Беллман Р., Дрейфус С. Прикладные задачи динамического программирования. Перевод с англ. – М.: Наука, 1965. – 459 с.
©Скворчевський О.Є., 2011
