18

Лабораторна робота 5 елементи математичної статистики. Нелінійна регресія і кореляція

1. Мета роботи

1. Вивчити основні поняття математичної статистики

2. Вивчити основні поняття кореляційно-регресійного аналізу

3. Освоїти методи вибору виду залежності і оцінки якості отриманого рівняння

4. Навчитися використовувати MS Excel при побудові і аналізі регресійних моделей.

відносних частот.

3. Знайти емпіричну функцію розподілу і побудувати її графік.

4. Обчислити вибіркове середнє значення і незміщену оцінку дисперсії . Висунути гіпотезу про можливий закон розподілу.

5. Знайти частоти закону розподілу і перевірити справедливість гіпотези про закон розподілу за допомогою критерію Пірсона при рівні значущості .

6. Знайти довірчий інтервал для математичного сподівання

2. Короткі теоретичні відомості

2.1. Основні формули математичної статистики

1. Оцінка для математичного сподівання (вибіркова середня)

.

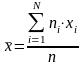2. Незміщена та зміщена оцінки дисперсії

.

3. Для нормального розподілу інтервал довіри для математичного сподівання (вибіркової середньої) при невідомому значенні середньоквадратичного відхилення та при відомому вибірковому має вигляд:

,

де число знаходимо за таблицями розподілу Стьюдента (дивись додатки) за заданою надійністю і числом ступенів свободи .

4. Для нормального розподілу справедлива формула для границь довірчого інтервалу для дисперсії при довірчій ймовірності (надійності) :

де – значення випадкової величини, що має розподіл (хі квадрат Пірсона) з числом ступенів свободи при рівні значущості , де

- значення випадкової величини, що має розподіл з числом ступенів свободи при рівні значущості .

Вивчивши цей розділ, студент повинен знати поняття вибірки, статистичного розподілу, означення незміщеної, ефективної і спроможної оцінок параметрів розподілу, поняття довірчого інтервалу та статистичної перевірки гіпотез. Він повинен вміти побудувати статистичний розподіл, полігон частот (відносних частот), емпіричну функцію розподілу F*(x), знайти оцінки для математичного сподівання (вибіркову середню), визначити незміщену та зміщену оцінку дисперсії, знайти границі довірчого інтервалу для математичного сподівання та дисперсії при довірчій ймовірності (надійності) , побудувати інтервальний статистичний розподіл вибірки, збудувати гістограму відносних частот.

Студент повинен вміти застосовувати на практиці ці знання для знаходження оцінки статистичних характеристик та параметрів генеральної сукупності, яка розподілена нормально (або має статистичний розподіл, близький до показникового розподілу, біноміального розподілу або розподілу Пуассона) за даними досліджень.

Оцінки, що визначаються одним числом, звуться точковими. Наприклад, вибіркова (статистична) середня (математичне сподівання), вибіркова (статистична ) дисперсія – точкові оцінки. У випадку малого числа спроб ці оцінки можуть привести до суттєвих помилок. У такому разі застосовуються інтервальні оцінки, що визначаються двома числами – границями інтервалу (що містить величину, яка оцінюється з заданою ймовірністю). Таким чином, задача зводиться до визначення такого інтервалу (його називають надійним або довірчим інтервалом), який з заданою ймовірністю (її називають надійністю) охоплює параметр, що оцінюється. Найчастіше надійність приймають рівною =0,95 або =0,99.

Розв’язання задач математичної статистики потребує великого обсягу обробки даних та обчислень. Відзначимо що потужним інструментарієм статистичної обробки даних володіють електронні таблиці Microsoft Excel. Дуже корисним і простим є використання й інших програм, наприклад: NUMERI, MATLAB, Mathcad, STATISTIKA, STATGRAFHICS.