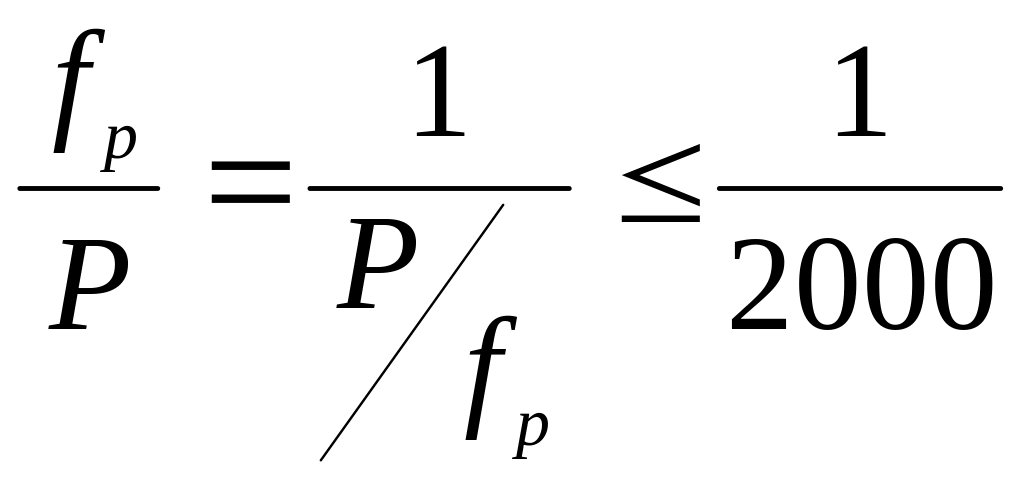Вычисление дирекционных углов сторон хода и приращений координат
1. Дирекционные углы линий вычисляют по правилу: дирекционный угол последующей стороны равен дирекционному углу предыдущей стороны плюс/минус 180°, минус горизонтальный угол справа по ходу лежащий, таким образом:
αΠΠ8-I = α0 + 180° − βΠΠ8 + 360°;
αI-II = αПП8-I − 180° − βI ;
αII-ПП19 = αI-II + 180° − βII .
2. Проконтролировать правильность вычисления дирекционных углов по конечному дирекционному углу αп, по дирекционному углу αII-ΠП19 последней стороны хода и уравненному углу βΠП19 при точке ПП19
αп = αII-ΠП19 + 180° - βΠП19
Вычисленное значение αп должно совпадать с заданным его значением по варианту.
3. Вычислить приращения координат между пунктами хода по формулам:
Δx = S · cosα;
Δy = S · sinα.
Горизонтальное проложение стороны хода ПП8 – I было вычислено при выполнении Задания № 1.
К заданию 2 Таблица 2
Ведомость вычисления координат точек теодолитно-высотного хода
|
||||||||||||||
Номер точки хода |
Измеренные углы β |
Уравненные углы βур |
Дирекцион-ные углы α |
Горизонтальное проложение S, м |
Приращения координат, м |
Координаты, м |
Номер точки хода |
|||||||
вычисленные |
уравненные |
х |
у |
|||||||||||
° |
′ |
° |
′ |
° |
′ |
∆х |
∆у |
∆хур |
∆уур |
|||||
1 |
2 |
3 |
4 |
5 |
6 |
7 |
8 |
9 |
10 |
11 |
12 |
|||
ПП7 |
- |
- |
- |
- |
|
|
- |
- |
- |
- |
- |
- |
- |
ПП7 |
ПП8 |
275 |
25,2 |
|
|
00,00 |
00,00 |
ПП8 |
|||||||
|
|
|
|
|
|
|
||||||||
|
|
|
|
|
|
|
|
|||||||
I |
69 |
32,5 |
|
|
|
|
170,82 |
|
|
|
|
|
|
I |
|
|
|
|
|
|
|
|
|||||||
II |
100 |
28,3 |
|
|
|
|
178,44 |
|
|
|
|
|
|
II |
|
|
|
|
|
|
|
|
|||||||
ПП19 |
135 |
21,6 |
|
|
|
|
- |
∑∆хв = |
∑∆ув = |
|
|
|
|
ПП19 |
ПП20 |
- |
- |
- |
- |
|
|
|
|
|
- |
- |
ПП20 |
||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
∑βизм |
|
|
|
|
Р = ∑S =
α0 – αп + 180° · п = |
∑∆хт = |
∑∆у т = |
|
|
|
||||
∑βт |
|
|
∑βт = |
|
|
|
|
XПП19 – XПП8 = |
||||||
ƒβ |
|
|
|
|
ƒх =
|
ƒу =
|
|
|
|
|||||
ƒβ доп |
|
|
ƒβ
доп = 1′ |
ƒр
=
|
|
|
YПП19 – YПП8 = |
|||||||
|
|
|
||||||||||||
|
|
|
|
|
|
|
||||||||
=
