
- •1 Растяжение стержня собственным весом
- •2 Кручение стержня
- •2.1 Ссылка: Феодосьев в. И. Сопротивление материалов. М., Наука, 1986, стр. 98, 106.
- •2.5 Данные для расчета.
- •2.6 Результаты расчета.
- •3 Изгиб консоли сосредоточенной силой
- •3.1 Ссылка: Феодосьев в. И. Сопротивление материалов. М., Наука, 1986, стр. 150, 159, 167.
- •3.5 Данные для расчета.
- •3.6 Результаты расчета.
- •4 Трехмерная задача теории упругости. Изгиб консоли
- •5 Изгиб двухопорной балки равномерно распределенной нагрузкой
- •6 Нагружение кругового стержня малой кривизны перпендикулярно его плоскости
- •7 Изгиб бруса большой кривизны
- •8 Изгиб круглой пластины равномерно распределенной нагрузкой
- •9 Изгиб прямоугольной пластины равномерно распределенной нагрузкой
- •10 Цилиндрическая оболочка под действием внутреннего давления
- •11 Коническая оболочка под действием внутреннего давления
- •12 Циллиндрическая оболочка с заделанными краями под действием внутреннего давления
- •13 Тонкостенный цилиндрический сосуд с полусферическими днищами под действием внутреннего давления
- •14 Растяжение стержня собственным весом
- •15 Трехмерная задача теории упругости. Изгиб консоли
- •16 Растяжение стержня собственным весом
- •17 Кручение стержня
- •18 Изгиб консоли сосредоточенной силой
- •19 Трехмерная задача теории упругости. Изгиб консоли
- •20 Изгиб двухопорной балки равномерно распределенной нагрузкой
- •21 Нагружение кругового стержня малой кривизны перпендикулярно его плоскости
- •22 Изгиб бруса большой кривизны
- •23 Изгиб круглой пластины равномерно распределенной нагрузкой
- •24 Изгиб прямоугольной пластины равномерно распределенной нагрузкой
- •25 Цилиндрическая оболочка под действием внутреннего давления
- •26 Коническая оболочка под действием внутреннего давления
- •27 Циллиндрическая оболочка с заделанными краями под действием внутреннего давления
- •28 Тонкостенный цилиндрический сосуд с полусферическими днищами под действием внутреннего давления
- •29 Растяжение стержня собственным весом
- •30 Трехмерная задача теории упругости. Изгиб консоли
- •31 Растяжение стержня собственным весом
- •32 Кручение стержня
- •33 Изгиб консоли сосредоточенной силой
- •34 Трехмерная задача теории упругости. Изгиб консоли
- •35 Изгиб двухопорной балки равномерно распределенной нагрузкой
- •36 Нагружение кругового стержня малой кривизны перпендикулярно его плоскости
- •37 Изгиб бруса большой кривизны
- •38 Изгиб круглой пластины равномерно распределенной нагрузкой
- •39 Изгиб прямоугольной пластины равномерно распределенной нагрузкой
- •40 Цилиндрическая оболочка под действием внутреннего давления
- •41 Коническая оболочка под действием внутреннего давления
- •42 Циллиндрическая оболочка с заделанными краями под действием внутреннего давления
- •43 Тонкостенный цилиндрический сосуд с полусферическими днищами под действием внутреннего давления
- •44 Растяжение стержня собственным весом
- •45 Трехмерная задача теории упругости. Изгиб консоли
- •46 Растяжение стержня собственным весом
- •47 Кручение стержня
- •48 Изгиб консоли сосредоточенной силой
- •49 Трехмерная задача теории упругости. Изгиб консоли
- •50 Изгиб двухопорной балки равномерно распределенной нагрузкой
- •51 Нагружение кругового стержня малой кривизны перпендикулярно его плоскости
- •52 Изгиб бруса большой кривизны
- •53 Изгиб круглой пластины равномерно распределенной нагрузкой
- •54 Изгиб прямоугольной пластины равномерно распределенной нагрузкой
L Задачи по курсу “Информационные технологии в разработке новой техники ” |
1 Растяжение стержня собственным весом
1.1 Ссылка: Феодосьев В. И. Сопротивление материалов. М., Наука, 1986, стр. 40.
1.2 Тип анализа: линейный статический анализ.
1.3 Типы конечных элементов: CROD, CBAR, CBEAM.
1.4 Постановка
задачи.
Определить растягивающее напряжение у заделки и перемещение свободного конца подвешенного цилиндрического стержня, нагруженного силами собственного веса (рис. 1). Длина стержня l, диаметр 500 мм.
1.5 Данные для расчета.
М
Рис. 1
одуль упругости материала E = 2105 МПа, коэффициент Пуассона = 0,3, плотность материала = 7850 кг/м3, ускорение свободного падения g = 9,81 м/с2, l = 100 м.1.6 Результаты расчета.
Величина |
Значение |
, МПа |
? |
u, мм |
? |
2 Кручение стержня
2.1 Ссылка: Феодосьев в. И. Сопротивление материалов. М., Наука, 1986, стр. 98, 106.
2.2 Тип анализа: линейный статический анализ.
2.3 Тип конечного элемента: CROD, CBAR, CBEAM.
2.4 Постановка задачи.
С
Рис. 2
тержень длиною l подвергается воздействию крутящего момента Mк, как показано на рис. 2 а. Форма поперечного сечения стержня – прямоугольник со сторонами a и b (рис. 2 б). Определить наибольшее касательное напряжение в стержне и угол поворота его сечения в месте приложения момента Mк.2.5 Данные для расчета.
Модуль упругости материала E = 2105 МПа, коэффициент Пуассона = 0,3, l = 1 м, a = 20 мм, b = 10 мм, Mк = 50 Нм.
2.6 Результаты расчета.
Величина |
Значение |
|
? |
|
? |
3 Изгиб консоли сосредоточенной силой
3.1 Ссылка: Феодосьев в. И. Сопротивление материалов. М., Наука, 1986, стр. 150, 159, 167.
3.2 Тип анализа: линейный статический анализ.
3.3 Типы конечных элементов: CBAR, CBEAM.
3 .4 Постановка
задачи.
.4 Постановка
задачи.
Консольная балка нагружена сосредоточенной силой P (рис. 3 а). Балка имеет длину l и поперечное сечение в форме стандартного швеллера № 10У (рис. 3 б). Сила P приложена в точке центра изгиба. Определить наибольшие (нормальное и касательное) напряжения в балке, а также прогиб в точке приложения силы P без учета сдвига продольных слоев.
3.5 Данные для расчета.
М
Рис. 3
одуль упругости материала E = 2105 МПа, l = 1м, P = 2 кН. Для швеллера № 10У h = 100 мм, b = 46 мм, s = 4,5 мм, t = 7,6 мм.3.6 Результаты расчета.
Величина |
Значение |
|
? |
, МПа |
? |
y, мм |
? |
4 Трехмерная задача теории упругости. Изгиб консоли
4.1 Ссылка: Тимошенко С. П., Гудьер Дж. Теория упругости. М., Наука, 1975, стр. 358.
4.2 Тип анализа: линейный статический анализ.
4.3 Типы конечных элементов: CTETRA4, CTETRA10, CHEXA8, CHEXA20.
4 .4 Постановка
задачи.
.4 Постановка
задачи.
К
Рис. 4
онсольная балка длиной l прямоугольного поперечного сечения нагружена сосредоточенной силой P (рис. 4). Определить наибольшие (нормальное и касательное) напряжения в балке.4.5 Данные для расчета.
Модуль упругости материала E = 2105 МПа, коэффициент Пуассона = 0,3, l = 1м, a = 10 мм, b = 20 мм, P = 2 кН.
4.6 Результаты расчета.
Величина |
Значение |
|
? |
|
? |
5 Изгиб двухопорной балки равномерно распределенной нагрузкой
5.1 Ссылка: Тимошенко С. П. Сопротивление материалов, т. 1. М., Наука, 1965, стр. 78, 152.
5.2 Тип анализа: линейный статический анализ.
5.3 Типы конечных элементов: CBAR, CBEAM.
5 .4 Постановка
задачи.
.4 Постановка
задачи.
Балка длиной l свободно оперта на концах и изгибается равномерно распределенной нагрузкой интенсивности q (рис. 5 а). Балка имеет поперечное сечение в форме стандартного двутавра № 12 (рис. 5 б). Определить наибольшее нормальное напряжение в балке, а также ее наибольший прогиб с учетом сдвига продольных слоев.
5.5 Данные для расчета.
М
Рис. 5
одуль упругости материала E = 2105 МПа, коэффициент Пуассона = 0,3, l = 700 мм, q = 50 кН/м. Для двутавра № 12 h = 120 мм, b = 64 мм, s = 4,8 мм, t = 7,3 мм.5.6 Результаты расчета.
Величина |
Значение |
, МПа |
? |
f, мм |
? |

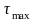 ,
МПа
,
МПа ,
рад
,
рад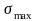 ,
МПа
,
МПа ,
МПа
,
МПа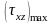 ,
МПа
,
МПа