MATHCAD_ИНОСТР_НОВАЯ2
.pdf
Пояснение
Если значения аргумента не указать, то MATHCAD создает график функции в пределах значений аргумента, по умолчанию принятых равными от –10 до 10.
Листинг 3.3. Построение нескольких зависимостей на одном графике
21
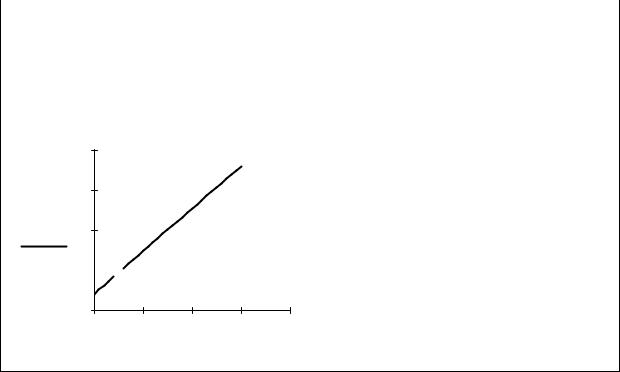
Пояснение
На одном графике может быть отложено до 16 различных зависимостей. Для этого в местозаполнитель по оси Y вводятся имена функций через запятую (y(x) , z(x) ).
3.2. Задачи для выполнения лабораторных работ
Листинг 3.4. Построить |
график |
функции y 2x lg(x) 0,5 в интервале |
2 x 5 с шагом h 0,1 |
|
|
|
|
|
|
|
|
x : 2,2.1 .. 5 |
Задание диапазона изменения переменной |
|
y(x) : 2 x log(x) |
0.5 |
Задание функции для построения |
графика |
||
12
10
y(x) 8
6
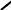
4
2 3 4 5 6
x
Варианты задач (часть1) представлены в табл.3.1.
Таблица 3.1. Варианты задач
№ |
Функция |
Диапазон изменения |
Шаг |
вар. |
|
переменной |
|
1 |
2 |
3 |
4 |
1 |
y sin(x) cos(x) |
x |
h 0,1 |
2 |
y x2 4 sin(x) |
x |
h 0,1 |
3 |
y x cos(x) 1 |
7 x 4,5 |
h 0,1 |
4 |
y 2 x cos(x) 7 |
x |
h 0,1 |
22
Окончание табл.3.1
1 |
2 |
3 |
4 |
5 |
y x lg(x 1) 3 |
0 x 15 |
h 0,1 |
6 |
y 2 ln(x) x 2 1 |
1 x 50 |
h 0,1 |
7 |
y x cos(x) 2 |
1,7 x 4,5 |
h 0,1 |
8 |
y x2 4 sin(x) |
x |
h 0,1 |
9 |
y x (x 4)2 9 |
0,5 x 7 |
h 0,1 |
10 |
y x4 x3 2 x2 3 x 52 |
0 x 6 |
h 0,1 |
11 |
y arctg(x) x3 |
5 x 10 |
h 0,1 |
12 |
y x sin(3x) 1 |
0 x 6 |
h 0,1 |
Варианты задач (часть 2)
1. Построить график зависимости скорости реакции по уравнению
K 78,56 e 0,1037 ; |
1 25; |
1 |
2. Построить график зависимости содержания влаги, x (в % от веса сухого остатка) от времени t (мин.) по уравнению
x 101,4568 0,00938t; |
0 t 100; |
t 5 |
3. Построить график зависимости между количеством раствора y – (в %), уносимого из выпарного аппарата, и его производительностью x – (в кг
ч) по уравнению:
y 5,789x2,071 10 7 0,048; |
250 x 2000; |
x 100 |
4. Построить график зависимости между атмосферным давлением p (в мм.рт.ст.) и барометрической высотой h (в км) по уравнению
p 760 10 0,0531h; |
0 h 6; |
h 0,2 |
5. Построить график зависимости между атмосферным давлением p (в мм.рт.ст.) и барометрической высотой h (в км) по уравнению
p 760 10 0,0531h; |
0 h 6; |
h 0,2 |
6. Построить график зависимости содержания влаги, x (в % от веса сухого остатка ) от времени t (мин) по уравнению
23
x 101,4568 0,00938t; |
0 t 100; |
t 5 |
7. Построить график изменения температуры воздуха в сушилке T в течение суток по уравнению
T 80 14,99cos(15 37) 18cos(30 353),
где – часы |
0 24 |
8. Построить график зависимости растворимости натриевой соли хлорноватистой кислоты в воде x (в г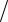
100г воды) от температуры t (в ºС) по уравнению
x 7,894e0,1939t 4,82; |
0 t 60; |
t 2 |
9. Построить график зависимости коэффициента трения в трубах от значения критерия Re
|
0,398 |
; |
3000 Re 16000; |
Re 1000 |
|
Re0,254 |
|||||
|
|
|
|
10. Построить график зависимости объема воздуха, содержащегося в воде (в мл. измеренный при t ºC и 760 мм.рт.ст.) от температуры t ºC по уравнению
(t 5) |
( 1,386 0,0375t) 25,68; |
0 t 25; |
t 1 |
Трехмерные графики
Рассмотрим на простом примере функции z(x,y) технику построения трехмерных графиков (рис.3.2, 3.3).
Чтобы создать трехмерный график, требуется нажать кнопку с изображением любого из типов трехмерных графиков на панели инструментов Graph (График). В результате появится пустая область графика с тремя осями (рис. 3.2) и единственным местозаполнителем в нижнем левом углу. В этот местозаполнитель следует ввести имя z функции z(x,y) двух переменных для быстрого построения трехмерного графика (рис. 3.3)
24
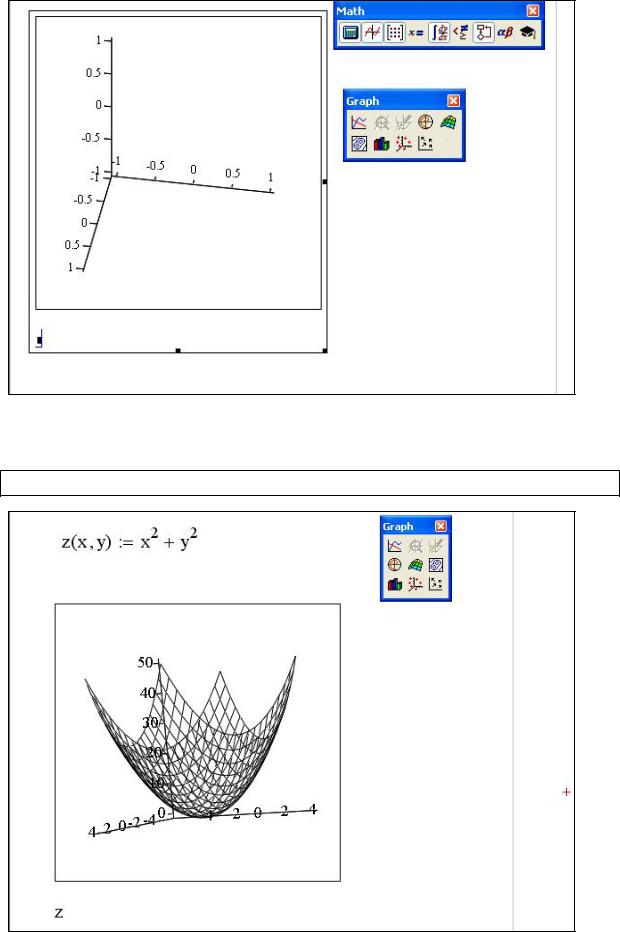
Рис. 3.2. Создание трехмерного графика
Листинг 3.5. Построение трехмерного графика
25
Листинг 3.6. Построение трехмерного графика
Листинг 3.7. Построение трехмерного графика
26
ТЕМА 4 Вычислительные операторы. Численное вычисление производных и
определенных интегралов. Символьные вычисления.
4.1. Краткие теоретические сведения
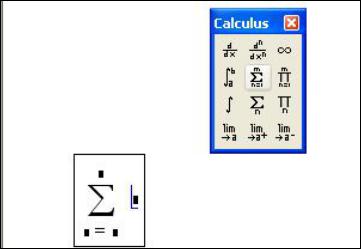
Вычислительные операторы вставляются в документы при помощи панели инструментов Calculus (Вычисления) (рис. 4.1). При нажатии любой из кнопок в документе появляется символ соответствующего математического действия, снабженный несколькими местозаполнителями. Количество и расположение местозаполнителей определяется типом оператора и в точности соответствует их общепринятой математической записи. Например, при вставке оператора суммы (см. рис. 4.1) необходимо задать четыре величины: переменную, по которой надо произвести суммирование, нижний и верхний пределы, а также само выражение, которое будет стоять под знаком суммы.
Для того чтобы вычислить неопределенный интеграл, следует заполнить два местозаполнителя: подынтегрального выражения и переменной интегрирования и т. д.
После ввода какого-либо вычислительного оператора имеется возможность вычислить его значение либо численно, нажатием клавиши <=>, либо аналитически, с помощью оператора символьного вывода < → >.
Рис. 4.1. Вставка оператора суммирования
27
Листинг 4.1. Вычислить значение выражения
4.2. Задачи для выполнения лабораторных работ
Листинг 4.2. Для приведенной функции y(x)=(x2 1) sin(x 0.5)
на заданном отрезке [–1, 1] вычислить:
значения дифференциала в точках, разбивающих отрезок с шагом 0.5;
интеграл функции на отрезке.
|
x : 1, 0.5 .. 1 |
|
Задание начальной, конечной и |
|||
|
|
промежуточных точек отрезка |
||||
|
|
|
|
|
|
|
|
y(x) : x2 1 sin(x 0.5) |
Задание функции |
||||
|
d |
y(x) |
Вычисление производной |
|||
|
|
|||||
|
dx |
|
|
в заданных точках |
||
|
2.136 |
|
|
|
|
|
|
|
|
|
|
|
|
|
1.517 |
|
|
|
|
|
|
|
|
|
|
|
|
|
0.878 |
|
|
|
|
|
|
|
|
|
|
|
|
|
1.25 |
|
|
|
|
|
|
|
|
|
|
|
|
|
2.714 |
|
|
|
|
|
|
|
|
|
|
|
|
|
1 |
y(x) dx 1.036 |
Вычисление значения интеграла |
|||
|
|
|||||
|
|
|
|
на заданном отрезке |
||
|
1 |
|
|
|||
Варианты задач представлены в табл.4.1.
28
Таблица 4.1. Варианты задач
Вариант |
|
|
F(x) |
Интервал |
|||
1 |
|
0.37esin(x) |
[0, 2] |
||||
2 |
0.5x xlg(x) |
[1, 3] |
|||||
3 |
1 |
|
|
|
[1, 3] |
||
|
|
x ln(x 2) |
|
|
|||
4 |
(x 1.9) sin(x 3) |
[0, 3] |
|||||
5 |
|
|
3 cos(x) |
[1, 3] |
|||
|
|
|
2x |
|
|
||
6 |
|
|
2x |
[–2, 0] |
|||
|
|
|
cos(x 2) |
|
|
||
7 |
2.6x2 ln(x) |
[1, 3] |
|||||
8 |
|
x2 cos(x 4) |
[2, 4] |
||||
9 |
|
3x ln(x) |
[1, 4] |
||||
10 |
|
x2tg(x 2) |
[1, 3] |
||||
11 |
1.3x2 lg(x) |
[1, 3] |
|||||
12 |
(x 4) sin(x 0.1) |
[1, 3] |
|||||
29
Листинг 4.3. Символьное вычисление неопределенного интеграла.
Рисунок 4.2. Символьное вычисление неопределенного интеграла
Пояснение:
Для того чтобы найти неопределенный интеграл, щелкните по свободному месту в рабочем документе, затем в панели Calculus (Вычисления) по кнопке , введите с клавиатуры в помеченных
позициях выражение для функции и имя переменной интегрирования, заключите все выражение в выделяющую рамку и щелкните по символу <→> панели математики Symbolic Keyword Toolbar (Панель символики) или по символу <→> панели Evaluation (Выражения).
30