Задача 2. Зразок розрахунку просторового брусу

Дано:

Побудова епюр внутрішніх силових факторів

• ділянка DK.

Вважаємо, що ділянка DK жорстко закріплена в точці D.

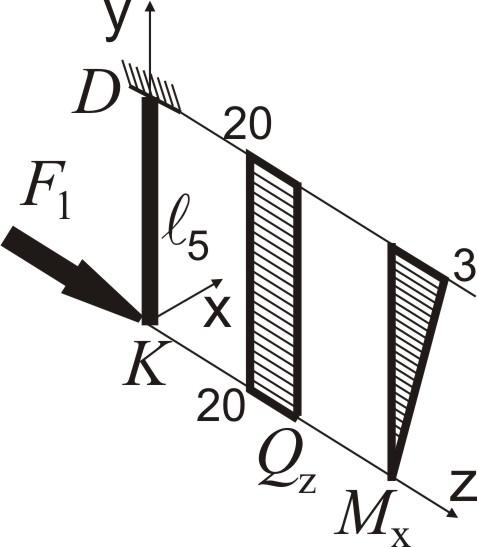
Вирази для внутрішніх силових факторів:

• згинальний момент:

Епюра згинального моменту будується в площині (YOZ), на стислих волокнах.

• поперечна сила:

• ділянка СD.

Вважаємо, що ділянка СD жорстко закріплена в точці С. Силу приводимо до точкиD з додатковим моментом в площині .

Вирази для внутрішніх силових факторів:

• згинальні моменти:

Епюри згинальних моментів будуються у відповідних площинах, на стислих волокнах.

• поперечні сили:

• крутний момент:

• ділянка BC.

Вважаємо, що ділянка BC жорстко закріплена в точці B. Всі навантаження з точки D приводимо до точки С. При цьому виникають додаткові моменти в площині від дії сили та в площині від дії сили . Момент переноситься вздовж осі без змін.

Вирази для внутрішніх силових факторів:

• згинальні моменти:

Епюри згинальних моментів будуються у відповідних площинах, на стислих волокнах.

• поперечні сили:

• поздовжня сила:

• крутний момент:

• ділянка LB.

Вважаємо, що ділянка LB жорстко закріплена в точці B.

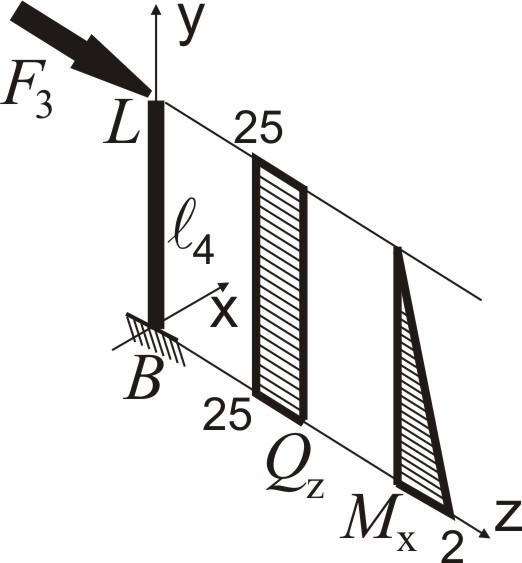
Вирази для внутрішніх силових факторів:

• згинальний момент:

Епюра згинального моменту будується в площині (YOZ) на стислих волокнах.

• поперечна сила:

• ділянка OB.

Ділянка OB жорстко закріплена в точці O. Всі навантаження переносимо в точку B з точок С та L.

Силу приводимо до точкиB з додатковим моментом в площині .

Сила приводиться до точкиB з додатковим моментом в площині .

При приведенні сили до точкиB виникає додатковий момент в площині .

Моменти , , та сила переносяться вздовж осіZ без змін.

Моменти, що лежать в одній площині алгебраїчно сумуються:

в площині ;

в площині .

Сума сил тапозначається як.

Вирази для внутрішніх силових факторів:

• згинальні моменти:

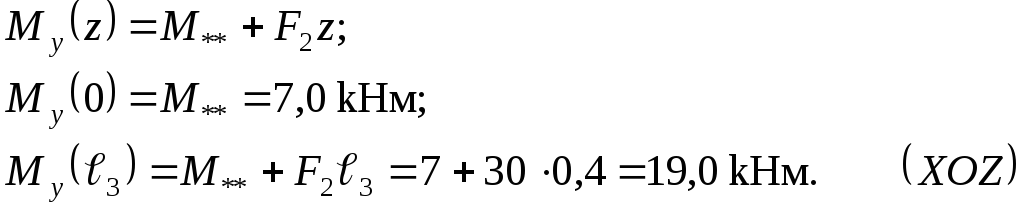
Епюри згинальних моментів будуються у відповідних площинах, на стислих волокнах.

• поперечні сили:

• поздовжня сила:

• крутний момент:

Сумарні епюри внутрішніх силових факторів просторового бруса:

• згинальний момент

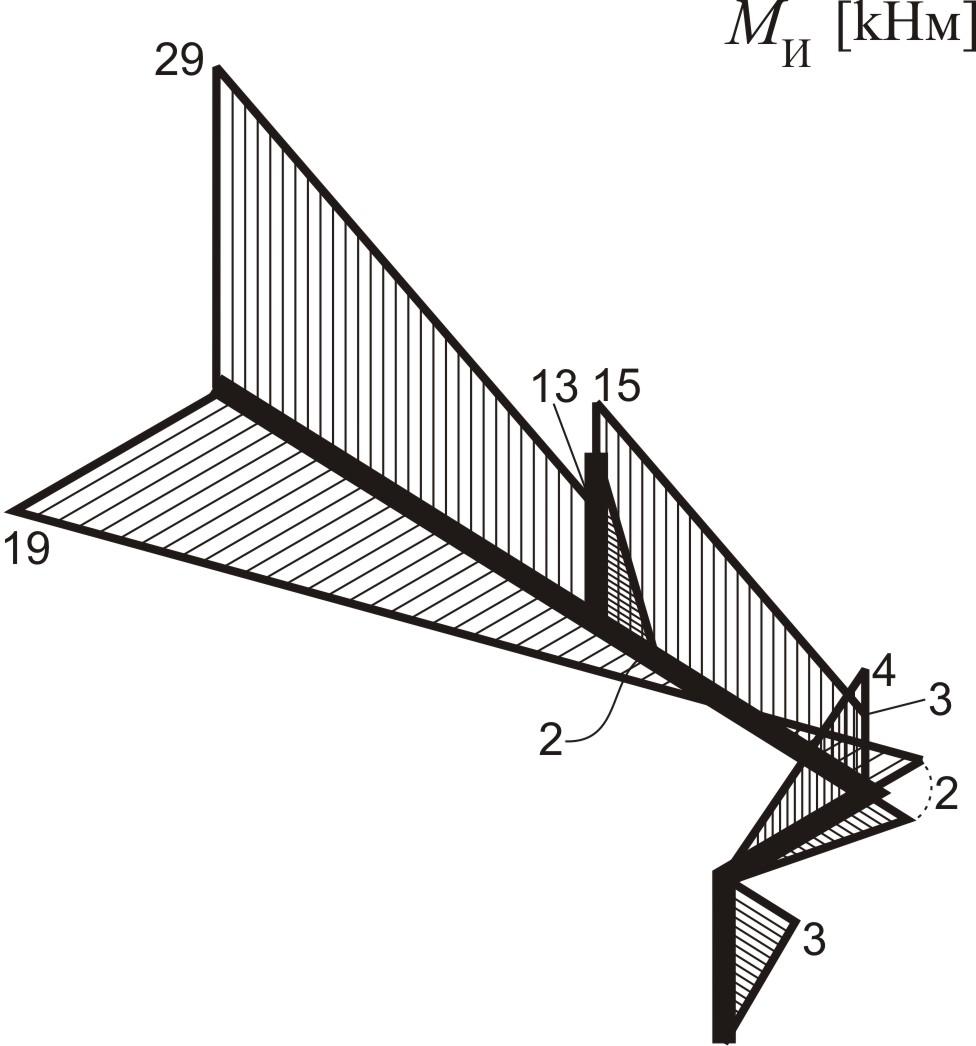
• поперечна сила

• крутний момент

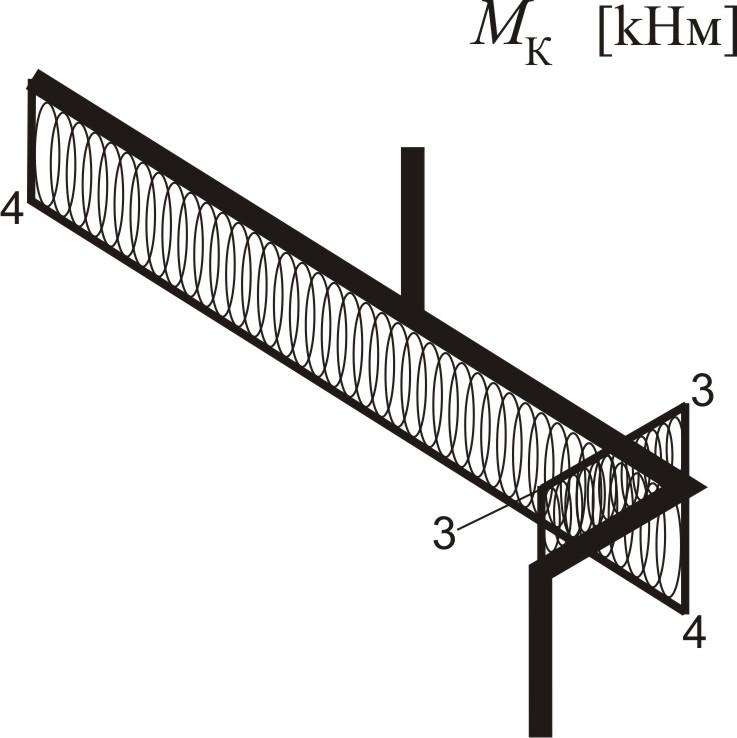
• поздовжня сила

Внутрішні зусилля в перерізі ОО:

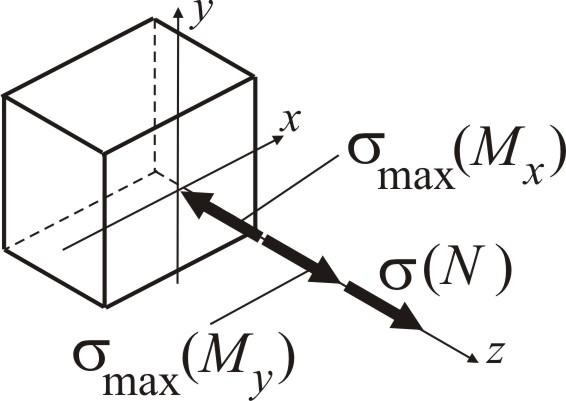
Визначення геометричних характеристик поперечного перерізу

Визначення максимальних значень компонент напружень

Побудова епюр напружень в поперечному перерізі

Визначення найнебезпечнішої точки поперечного перерізу

Точка 1

Напружений стан – лінійний (одновісний)

Точка 2

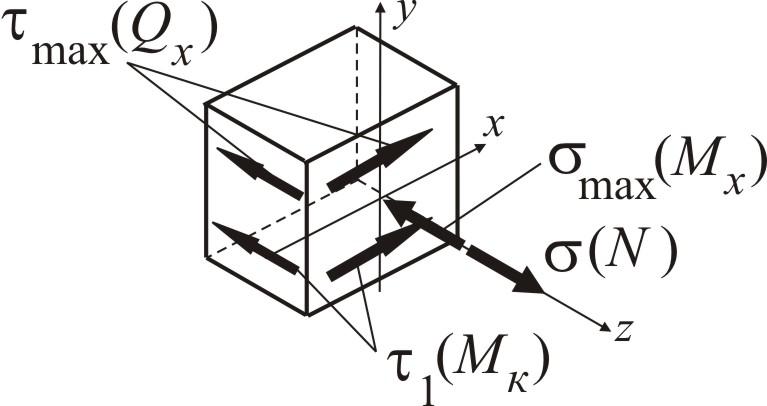
Напружений стан – плоский (двовісний).

Точка 3

Напружений стан – лінійний (одновісний)

Точка 4

Напружений стан – плоский (двовісний).

Точка 5

Напружений стан – лінійний (одновісний)

Точка 6

Напружений стан – плоский (двовісний).

Точка 7

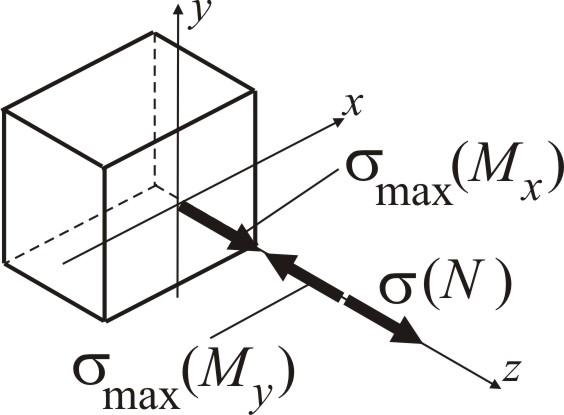
Напружений стан – лінійний (одновісний)

Точка 8

Напружений стан – плоский (двовісний).

Визначення коефіцієнта запасу

–умова міцності виконується.