Особенности расчета за пределами упругости.
1) За пределами
упругости неприменим принцип независимости
действия сил. Рассмотрим простой пример.
Стержень подвергается действию сил,
приложенных по его оси. Направление сил
разное.
.
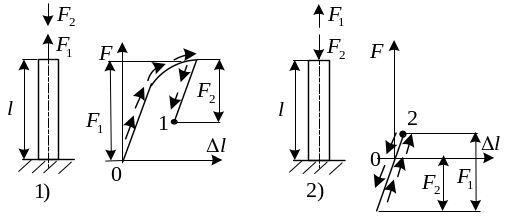
В первом случае
вначале прикладывается сила
,
а затем
.
Во втором случае наоборот. Мы видим, что
состояние системы в этих случаях
совершенно различно, т.е. порядок
приложения сил существенен.
2) Загружая конструкцию таким образом, чтобы материал ее работал за пределами упругости, и разгружая затем ее, мы приходим к такому положению, что напряжения и деформации не исчезают после снятия нагрузки. Появляются остаточные напряжения и остаточные деформации.
Эти величины во многих случаях представляют интерес. Они могут быть определены с помощью закона об упругой разгрузке.
Закон упругой разгрузки - для того, чтобы определить остаточные напряжения (деформации, перемещения), возникающие в упруго-пластической системе после снятия нагрузки необходимо из фактических напряжений (деформаций, перемещений) имеющих место при данной нагрузке вычесть величины напряжений (деформаций, перемещений) вычисленные для данной силы в предположении что система работает упруго.
Предельное состояние системы, работающей на растяжение.
Состояние системы станет предельным в том случае, если в
ней потечет столько элементов, что система станет кинематически
изменяемой.
Н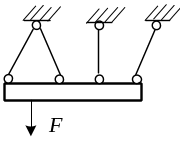
апример,
система, изображенная на рисунке перейдет
в предельное состояние в том случае,
если в ней потекут любые три стержня.
Разумеется, сто истинное предельное
состояние будет соответствовать
наименьшему значению силы, приводящей
систему в предельное состояние.
Значение нагрузки, отвечающей предельному состоянию, называют
предельной нагрузкой. Пример.
Лекция V Геометрические характеристики поперечных сечений.
При расчетах элементов инженерных конструкций приходится сталкиваться с необходимостью вычисления различных геометрических характеристик. Мы видим, что сила, которую может выдержать стержень на растяжение, пропорциональна площади поперечного сечения. Однако, площадь поперечного сечения не является исчерпывающей характеристикой. Сечения разной конфигурации могут иметь одинаковую площадь, но их поведение при изгибе или кручении будет различным. Простейший пример: полоса металла или бумаги, будучи согнутой (угловое сечение) приобретает способность сопротивляться изгибу в гораздо большей мере, чем такая же плоская полоса.
Для того, чтобы охарактеризовать геометрические свойства поперечных сечений стержней при таких нагружениях как изгиб, кручение и их комбинации, необходимо ввести более сложные характеристики – моменты площадей.
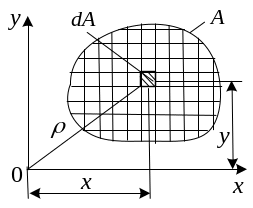
Рассмотрим
произвольное поперечное сечение с
площадью А. Выберем пока что
произвольную систему координат и любым
способом разобьем площадь сечения на
элементы. Если площадь произвольного
элемента
умножить
на его координату
то
мы получим элементарный момент первого
порядка.
Суммируя элементарные моменты по площади сечения А, и беря предел полученной интегральной суммы, получаем:
- статический
момент площади А относительно оси
x.
Аналогично можно ввести статический момент относительно оси y:
.
Подобным же путем можно получить еще
три момента второго порядка
;
;
Первые две величины называют осевыми моментами инерции соответственно относительно осей x и y.
- центробежный
момент инерции относительно осей х
и у.
Составим еще один
интеграл
,
который называ-
ется полярным
моментом инерции. Очевидно, что, т.к.
то
,
т.е. полярный момент инерции равен сумме
осевых.
Обратим
внимание на очевидный факт: осевые
моменты инерции
и полярный момент инерции
всегда положительны, а статические
моменты и центробежный момент инерции
могут принимать как положительные, так
и отрицательные значения.
Отметим еще некоторые свойства моментов:
1) момент (любой из моментов) составной площади равен сумме моментов ее частей.
2
)
Если фигура ограничена двумя замкнутыми
контурами, то ее момент можно вычислить,
вычитая из момента площади, ограниченной
внешним контуром, момент площади
ограниченной внутренним контуром.
3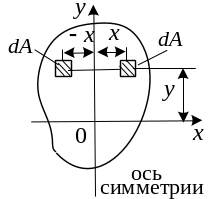
)
Если хотя бы одна из осей является осью
симметрии, то центробежный момент
инерции относительно данных осей
равняется нулю.
Это очевидно, т.к. фигуру можно представить как множество пар элементарных площадок, имеющих равными одну из координат и равными по величине и противоположными по знаку другую.