Лекция XV Расчет статически неопределимых балок.
Степень статической неопределимости балок легко подсчитывается. Она равняется (если балка неразрезная):
,
где
число опорных стержней.
Например:
Однако, еще проще убедиться в том, отбросив три опорных стержня. Если число пролетов балки невелико, особенно, если балка является однопролетной, то выбирать основную систему можно путем отбрасывания опор.
Пример.
В случае если балка многопролетная, то выбор основной системы путем отбрасывания опор себя не оправдывает.
Н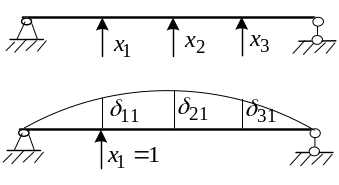
и
один из побочных коэффициентов в нуль
не обращается. Матрица коэффициентов
получается опорной и не содержит ни
одного нулевого элемента. Такая основная
система была исторически первой и хуже
ее придумать нельзя.
Уравнение 3-х моментов.
Выберем основную систему таким образом, чтобы неразрезная балка обратилась в совокупность однопролетных шарнирных опертых балок. Для этого разрежем сечения над опорами и вставим в разрезы шарниры. Т.к. врезав над опорами шарниры, мы устраним связь препятствующую взаимному повороту сечений в шарнире, то, понятно, что основные неизвестные у нас будут являться изгибающими моментами в опорных сечениях – опорными моментами.
Рассмотрим произвольную балку:
Пусть
- номера следующих друг за другом
произвольных опор, а
и
- пролеты, заключенные между данными
опорами. Составим каноническое уравнение
для
опоры:
Нетрудно заметить,
что только три коэффициента:
отличны от нуля, а остальные обращаются
в нуль.
Вычислим коэффициенты и свободные члены:
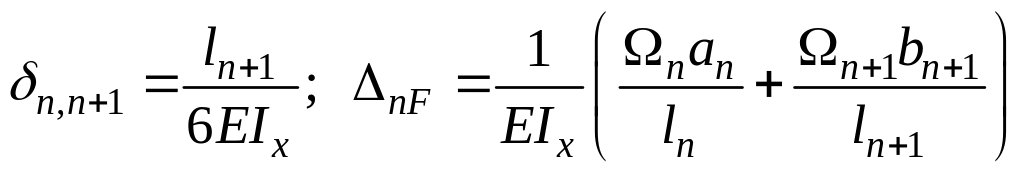
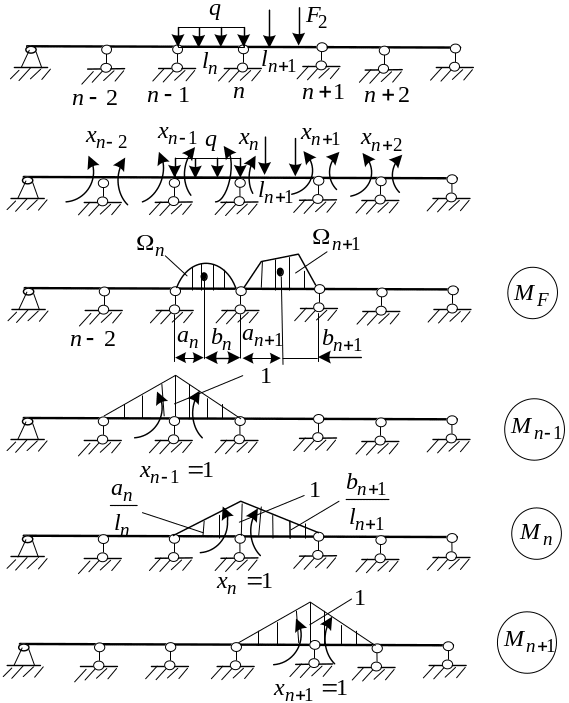
Подставим эти выражения в (1), умножим уравнение на 6 и
обозначим:
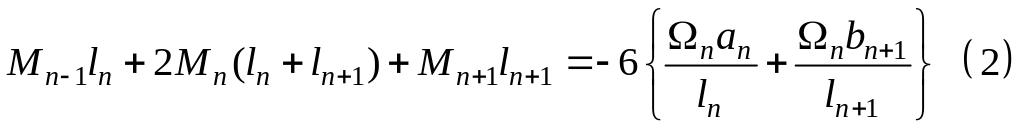Полученное
уравнение носит название “уравнение
трех моментов”,
и
- площади эпюр моментов в основной
системе следует рассматривать как
величины алгебраические и приписывать
им знак плюс в случае, если моменты
положительны, и знак минус в случае
отрицательных моментов.
С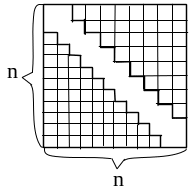
истема
канонических уравнений, составленных
таким образом, обладает тем преимуществом,
что какого бы порядка она не была, каждое
из уравнений будет содержать не более
3 неизвестных величин. Т.е. матрица
будет трехдиагональной (см. рисунок).
Ширина полосы равняется 3. Вне этой
полосы коэффициенты равны нулю, и они
не должны сохраняться в машинной памяти.
Задачи, приводимые к подобным матрицам,
эффективны для расчетов на ЭВМ, т.к. они
требуют меньшей машинной памяти и
меньшего времени для расчета.
При малой степени статической неопределимости эффективность применения уравнений (2) меньше, но тем не менее и здесь есть удобство, заключающееся в автоматической записи метода сил.
Лекция XVI Упруго-пластический изгиб. Чистый упруго пластический изгиб.
Р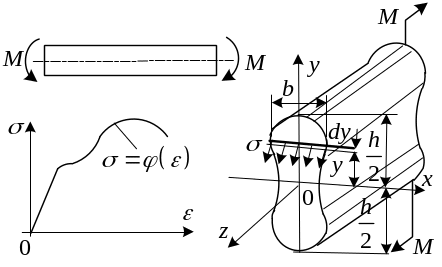
ассмотрим
стержень, работающий в условиях чистого
изгиба. Пусть поперечное сечение стержня
имеет две оси симметрии
и
.
Будем считать, что
материал одинаково работает как на
растяжение, так и на сжатие и нам задан
закон, связывающий напряжения с
деформацией:
В основу решения
положена гипотеза плоских сечений (см.
лекция 6).
или обозначим кривизну
Форма поперечного
сечения балки задается шириной:
где
вместо
аргумента
можно ввести безразмерную координату
и рассматривать функцию
.
Момент внутренних
сил, действующих на элементарную площадку
шириной
и высотой
(см.рис.) равняется:
Изгибающий момент
в сечении (учитывая, что ось
-ось
симметрии):
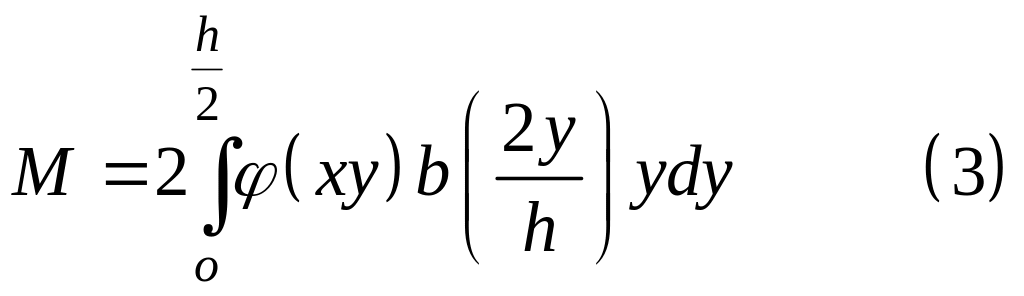
Выражение (3) можно
преобразовать, заменив переменную
интегрирования
на величину ей пропорциональную
.
Наибольшие деформации возникнут в точке
наиболее удаленной от оси
при
;
тогда
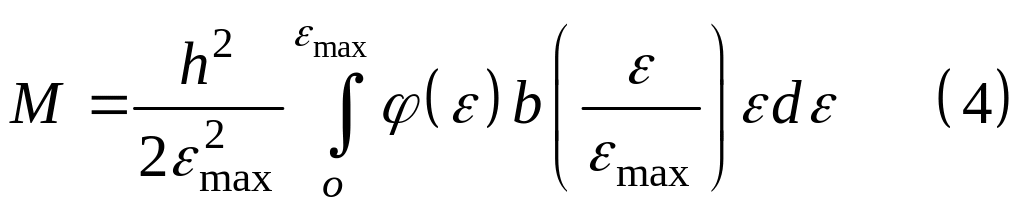
Интеграл
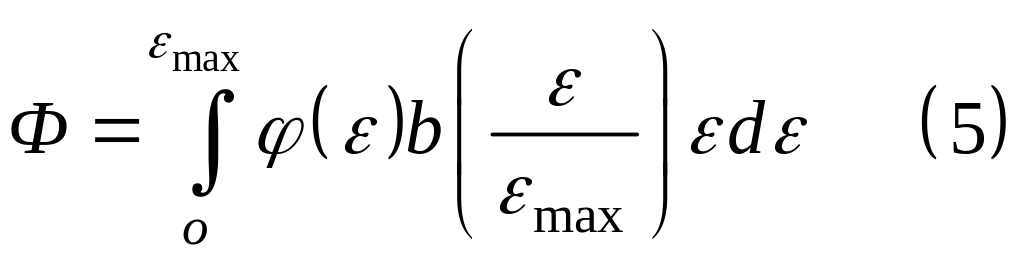может быть найден при
простом законе
и
аналитически, а в более сложных
случаях численно.
Таким образом, по
заданной кривизне
балки мы можем найти величину изгибающего
момента. Задаваясь различными значениями
кривизны
,
мы можем с помощью (4) найти соответствующие
им значения изгибающего момента
и построить график зависимости
от
.
И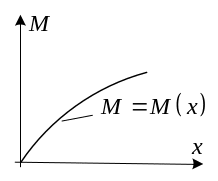
мея
этот график, можно по заданному моменту
найти величину
,
затем деформации по формуле
,
а по деформациям из закона
определить напряжения, возникающие в
поперечном сечении балки при заданном
моменте.