Лекция XIV Использование симметрии при расчете рам.
Если система имеет
три и более основных неизвестных, то
основную систему надо выбирать таким
образом, чтобы канонические уравнения
получились возможно более простыми,
т.е. чтобы матрица
(см. предыдущую лекцию) содержала возможно
больше нулевых элементов. Понятно, что
главные коэффициенты всегда отличны
от нуля, стало быть надо выбирать основную
систему таким образом, чтобы возможно
большее число побочных элементов
обратились
в нуль.
Значительных упрощений можно добиться, если система симметрична.
Р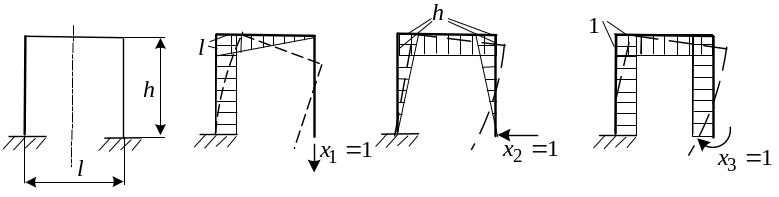
ассмотрим
в качестве примера простейшую симметричную
раму.
Нагрузку будем считать пока произвольной и на рисунке не
будем показывать. Если отбросить одну из заделок, то получится очень неудачная основная система. Ни один из коэффициентов системы в нуль не обратится.
В этом легко убедиться перемножая единичные эпюры. Выберем симметричную основную систему. Для чего разрежем раму по оси симметрии.
При таком выборе
основной системы часть неизвестных (
)
будет симметричной, а часть -
- кососимметричной. Соответственно
этому симметричными и кососимметричными
будут единичные эпюры. Перемножая
симметричную эпюру на кососимметричную,
получаем нуль. Поэтому
и система канонических уравнений будет
выглядеть:
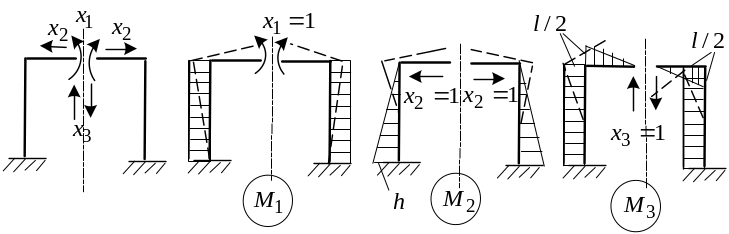
Таким образом, для симметричной системы всегда выгодно выбирать симметричную основную систему.
Пойдем дальше. Рассмотрим симметричную нагрузку. Например, показанную на рисунке.
П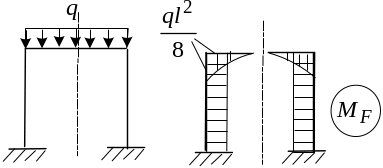
еремножая
эпюру
на
единичные эпюры, приходим к выводу:
Подставляя это в (1) получаем
а остальные неизвестные могут быть
найдены из двух первых уравнений.
2) Рассмотрим случай кососимметричной нагрузки.
В
этом случае
и (1) принимает вид:
;
;
Первые два уравнения представляют собой линейную одно
р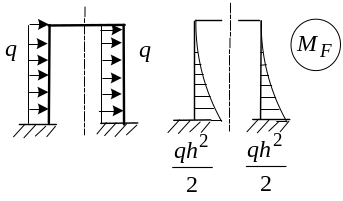
одную
систему, и т.к.
(больше того можно показать, что
определитель всегда положителен), то
система имеет лишь тривиальное решение:
Из третьего уравнения следует
.
Рассмотренные здесь особенности характерны для любых симметричных систем, а поэтому имеет место:
Правило:
Если система симметрична и для ее расчета выбрана симметричная основная система, то при действии симметричной нагрузки кососимметричные неизвестные обращаются в нуль, а в случае кососимметричной нагрузки в нуль обращаются симметричные неизвестные.
В заключение отметим, что, если на симметричную систему действует произвольная нагрузка, то ее всегда можно представить в виде суммы нагрузки симметричной и кососимметричной нагрузки. Например:
Пример:
Определение перемещений
в статически неопределимых системах.
Для того , чтобы определить перемещение в статически неопределимой системе (раме, балке) нужно вначале раскрыть статическую неопределимость и построить эпюру моментов, Перемножая по правилу Верещагина эпюры, получаем искомое перемещение.
Пример.
Проверка правильности раскрытия
статической неопределимости.
Для того, чтобы проверить правильно ли построена эпюра моментов в статически неопределимой системе, поступают следующим образом. Берут основную систему и прикладывают единичные силы по направлению отброшенных связей и строят единичные эпюры. Перемножая проверяемую эпюру на любую единичную, мы должны получить в результате нуль, т.к. определяем перемещение по направлению связи. Пример.