Напряжения при поперечном изгибе.
При поперечном изгибе, помимо изгибающего момента, в поперечном сечение имеется также и поперечная сила, которая является результирующей элементарных усилий, действующих в плоскости сечения. Т.е. помимо нормальных напряжений возникают и касательные напряжения.
Касательные
напряжения искривляют поперечные
сечения и гипотеза плоских сечений,
вообще говоря, не выполняется. Однако
если длина велика по сравнению с высотой
балки, то искривления поп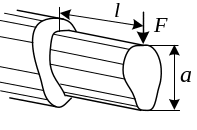
еречных
сечений и возникающее в случае поперечного
изгиба взаимное нажатие волокон не
оказывают существенного влияния на
величину нормальных напряжений, и
нормальные напряжения при поперечном
изгибе будут определяться по тем же
формулам, что и при чистом изгибе.
Дадим грубую оценку касательных напряжений при изгибе.
Пусть - длина балки, а
- характерный размер поперечного сечения.
Если сечение не
является тонкостенным, то площадь его
отличается от величины
числовым
множителем порядка единицы. Тогда
среднее касательное напряжение в сечении
имеет порядок
Оценим порядок нормальных напряжений.
Наибольший момент
имеет порядок
,
а момент сопротивления порядок
(например для прямоугольного сечения
).
Таким образом нормальное напряжение
имеет следующий порядок:
,
откуда видно, что если длина стержня
велика по сравнению с характерным
размером поперечного сечения
,
то касательные напряжения при расчетах
на прочность обычно не принимаются во
внимании. Однако, исключения составляют
случаи:
1) Тонкостенные стержни
2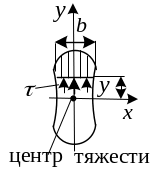
)
В случае конструкций, выполненных из
материалов с малым сопротивлением
межслойному сдвигу, например, древесина,
или, получающие в настоящее время большое
распространение армированные пластики,
когда касательные напряжения могут
оказаться более опасными, чем нормальные.
3) Для расчета соединений (поясных швов, заклепок) в металлических балках составного сечения.
Имея это ввиду, мы
приведем формулу для определения
касательных напряжений при изгибе,
полученную нашим соотечественником
Д.И.Журавским в середине прошлого века.
,
где
- касательные напряжения в слое, отстоящим
от нейтральной оси
на расстоянии
.
- поперечная сила в сечении.
- статический
момент части сечения, расположенной
выше слоя в котором определяются
касательные напряжения относительно
оси
.
- момент инерции
относительно оси
.
Следует иметь ввиду, что формула приближена и дает приемлемые результаты для высоких узких сечений.
Расчет на прочность при изгибе.
Расчет в упругой
стадии по методу допускаемых напряжений
ведется из условия
где
- допускаемое напряжение.
Легко понять, что более экономичными будут те сечения, которые при одном и том же расходе материала (одинаковой площади сечения) будут обладать большим моментом сопротивления. Пример неудачных сечений: круг, прямоугольник; эффективных сечений – двутавр.
Лекция X
Косой изиб. Внецентренное растяжение и сжатие.
Рассмотренный в прошлой лекции случай изгиба, когда изгибающий момент действует в плоскости главных осей инерции, называют часто прямым изгибом.
О
днако
во многих случаях указанное выше условие
не выполняется, например, в показанных
на рисунках примерах.
Определение:
Изгиб, когда плоскость действия изгибающего момента в сечении не совпадает с плоскостью главных центральных моментов, инерции называют косым изгибом.