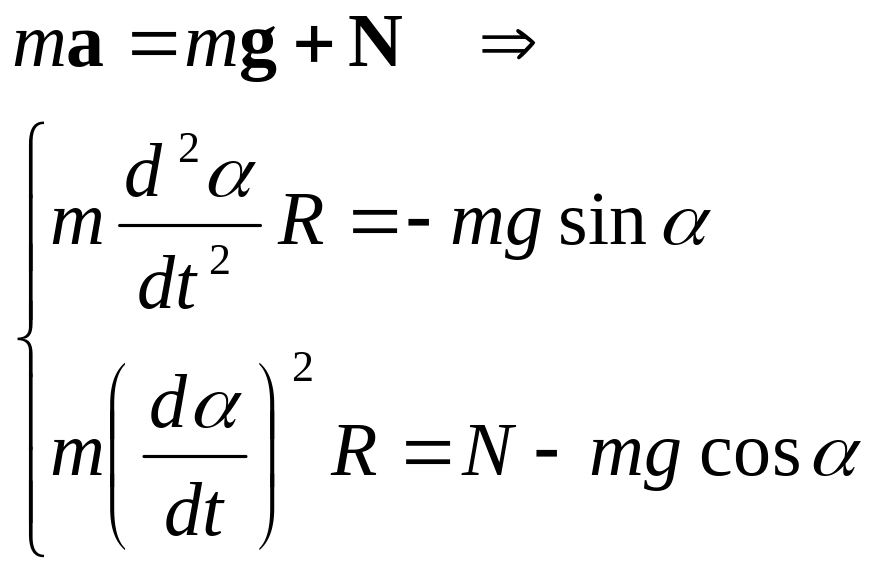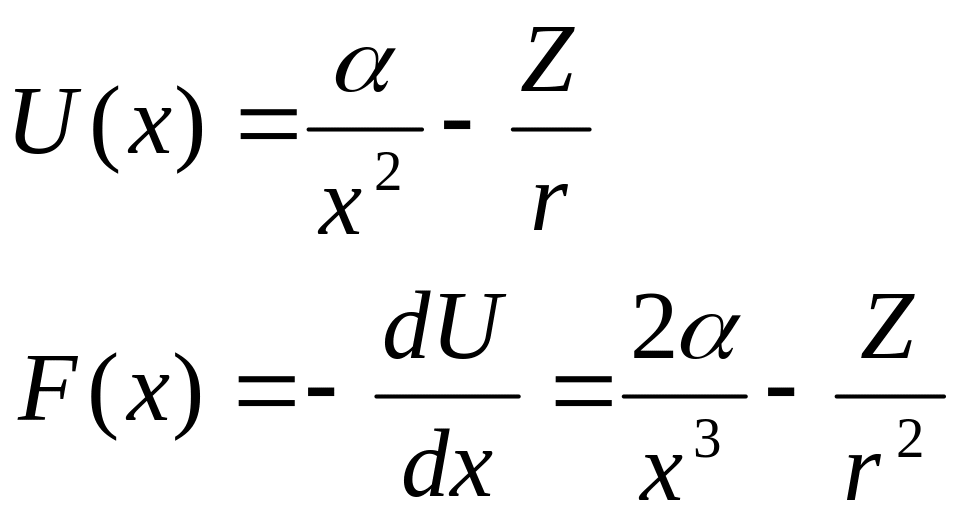- •Лекция 1 Введение: основные принципы классической и релятивистской механики
- •Вопросы и задачи для самостоятельной работы
- •Лекция 2 Кинематика. Основные понятия
- •2.1. Перемещение. Средняя и мгновенная скорости
- •2.2. Ускорение материальной точки
- •2.3. Равноускоренное движение
- •2.4. Классический закон сложения скоростей и ускорений
- •2.5. Преобразования Галилея
- •Вопросы и задачи для самостоятельной работы
- •Лекция 3 Кинематика криволинейного движения
- •3.1. Скалярное произведение. Базис
- •3.2. Путь, проходимый материальной точкой
- •3.3. Векторное произведение
- •3.4. Угловая скорость и угловое ускорение
- •3.5. Нормальное и тангенциальное ускорения
- •Вопросы и задачи для самостоятельной работы
- •Лекция 4 Основы динамики материальной точки
- •4.1. Законы Ньютона
- •4.2. Импульсная формулировка второго закона Ньютона
- •4.3. Второй закон Ньютона как уравнение движения
- •4.4. Прямая задача механики
- •4.5. Обратная задача механики (случай явной зависимости силы от времени)
- •Вопросы и задачи для самостоятельной работы
- •Лекция 5 Одномерное движение под действием сил, зависящих от положения и скорости тела, в простейших случаях
- •5.1. Случай силы, зависящей только от скорости и сонаправленной с ней
- •5.2 Падение тела в вязкой среде
- •5.3. Одномерное движение частицы под действием силы, зависящей от координаты
- •5.4. Движение, описываемое линейным дифференциальным уравнением с постоянными коэффициентами
- •5.5. Движение, описываемое нелинейным дифференциальным уравнением (реальный маятник)
- •5.6. Классическая частица в одномерной потенциальной яме
- •Вопросы и задачи для самостоятельной работы
- •Лекция 6 Примеры движения в трехмерном пространстве под действием сил, зависящих от положения и скорости тела
- •6.1. Движение тела, брошенного в вязкой среде под углом к горизонту
- •6.2. Движение тела под действием силы Лоренца
- •6.3. Движение заряженной частицы в скрещенных постоянных магнитном и электрическом полях
- •6.4. Движение в кулоновском поле
- •6.5. Примеры численного интегрирования движения в центральных и произвольных силовых полях
- •Вопросы и задачи для самостоятельной работы
- •Лекция 7 Законы сохранения в динамике материальной точки
- •7.1. Закон сохранения импульса
- •7.2. Закон сохранения момента импульса
- •7.3. Работа. Теорема об изменении кинетической энергии
- •7.3. Примеры вычисления работы различных сил
- •7.4. Потенциальная энергия, закон сохранения механической энергии
- •7.5. Вычисление потенциальных сил по известной потенциальной энергии
- •Вопросы и задачи для самостоятельной работы
- •Лекция 8 Движение в центральном и кулоновском поле
- •8.1. Закон всемирного тяготения
- •8.2. Гравитационное поле простейших симметричных распределений масс
- •8.3.Центробежный потенциал
- •8.4. Движение в кулоновском поле
- •8.5. Третий закон Кеплера
- •Вопросы и задачи для самостоятельной работы
- •Лекция 9 Динамика системы материальных точек
- •9.5. Закон сохранения механической энергии в потенциальных системах
- •Лекция 10 Примеры движения систем классических материальных точек
- •10.1. Задача двух тел
- •10.2. Упругое столкновение двух тел. Лобовой удар
- •10.3. Произвольное упругое столкновение
- •10.4. Неупругие и сверх упругие столкновения
- •10.5. Движение тела с переменной массой
- •Вопросы и задачи для самостоятельной работы
- •Лекция 11 Симметрии и законы сохранения в механике
- •11.1. Симметрия относительно трансляций и закон сохранения импульса
- •11.2. Симметрия относительно поворотов и закон сохранения момента импульса
- •11.3. Однородность времени и закон сохранения энергии
- •11.4. Экстремальные принципы в механике
- •11.5. Другие симметрии и глобальные законы сохранения в физике
- •Лекция 12 Абсолютно твердое тело. Статика
- •12.1. Определения
- •12.2. Равнодействующая сил, приложенных к твердому телу
- •12.3. Статика
- •12.5. Произвольное движение твердого тела. Теорема Эйлера
- •Вопросы и задачи для самостоятельной работы
- •Лекция 13 Абсолютно твердое тело. Динамика
- •13.1. Момент импульса твердого тела, тензор инерции
- •13.2. Кинетическая энергия
- •13.3. Вращение твердого тела вокруг закрепленной оси
- •13.4. Свободное вращение твердого тела
- •13.5. Вращающееся тела под воздействие внешних сил
- •Вопросы и задачи для самостоятельной работы
- •Лекция 14 Релятивистская кинематика
- •14.1. Необходимость перехода к релятивистскому описанию
- •14.2. Постулаты сто. Синхронизация часов. Измерение расстояний. Относительность одновременности
- •14.3. Релятивистские эффекты замедления времени и сокращения длин отрезков
- •14.4. Преобразования Лоренца
- •14.5. Четырехмерное пространство-время
- •Вопросы и задачи для самостоятельной работы
- •Лекция 15 Релятивистская динамика
- •15.1. Релятивистски инвариантное описание при помощи четырехвекторов
- •15.2. Четырехскорость
- •15.3. Четырехимпульс и четырехсила
- •15.4. Релятивистский закон преобразования сил и основной закон релятивистской динамики
- •15.5. Релятивистская энергия
- •Вопросы и задачи для самостоятельной работы
- •Лекция 16 Движение в неинерциальных системах отсчета
- •16.1. Сила инерции
- •16.2. Силы инерции во вращающихся системах отсчета
- •16.3. Маятник Фуко
- •16.4. Принцип эквивалентности и современные представления о природе гравитационных сил
- •16.5. Приливообразующие силы
- •Вопросы и задачи для самостоятельной работы
- •Лекция 17 Колебательные системы с одной степенью свободы
- •17.1. Вывод простейшего уравнения гармонических колебаний
- •17.2. Решение простейшего уравнения незатухающих гармонических колебаний
- •17.3 Энергетические соотношения. Фазовая диаграмма
- •17.4. Затухающие колебания
- •17.5. Апериодический режим при затухающих колебаниях
- •Лекция 18 Вынужденные колебания в линейной одномерной системе
- •18.1. Уравнение вынужденных колебаний
- •18.2. Установившиеся колебания
- •18.3. Превращения энергии при установившихся вынужденных колебаниях
- •Лекция 19 Связанные маятники
- •19.1. Постановка задачи
- •19.2. Решение системы уравнений связанных колебаний.
- •19.3. Вынужденные колебания связанных маятников
- •19.4. Бесконечная цепочка из связанных маятников
- •Лекция 20 Механика упругих тел
- •20.1. Упругие напряжения
- •20.2. Растяжение и сжатие
- •20.3. Объемное сжатие и растяжение
- •20.4. Скорость распространения возмущения в стержне
- •Лекция 21 Волны в безграничной среде
- •21.1. Классификация волн
- •21.2. Поперечные волны в натянутом шнуре
- •21.2.Продольные волны в упругой среде
- •21.3. Энергия в упругой волне
- •21.4. Плоские монохроматические волны
- •Лекция 22 Волны в ограниченной среде
- •22.1. Отражение волн от закрепленного конца струны
- •22.2. Сложение двух монохроматических волн
5.5. Движение, описываемое нелинейным дифференциальным уравнением (реальный маятник)
|
|
(5.25) |
Уравнение движения реального маятника. |
|
(5.26) |
Уравнение в стандартных обозначениях. |
|
|
Рис. 5.3. При малых начальных скоростях колебания оказываются близкими к гармоническим, поскольку входящий в уравнение движения синус может быть аппроксимирован линейной функцией, что приводит к уравнению, тождественному уравнению гармонических колебаний (5.17). |
||
|
Рис. 5.4. При приближении начальной скорости к критическому значению, соответствующему энергии перехода системы в состояние неустойчивого равновесия, колебания начинают резко отличаться от гармонических: в области изменения направления движения (поворота) тело проводит аномально большое время. |
||
|
Рис. 5.5. При превышении начальной скоростью критического значения колебательный режим принципиально меняется: маятник начинает вокруг точки подвеса с угловой скоростью, сильно зависящей от положения груза. |
||
|
Рис. 5.6. При больших начальных скоростях незначительные изменения скорости, вызванные действием на маятник силы тяжести, становятся малосущественными. |
||
5.6. Классическая частица в одномерной потенциальной яме
|
|
(5.27) |
Потенциальная яма, обусловленная кулоновскими взаимодействиями и центробежными эффектами. |
|
|
Рис. 5.7. Попытка получения аналитического решения для движения в потенциальной яме. Обратить уравнение относительно времени при помощи пакета «Математика» не приносит успеха. |
|||
|
Рис. 5.8. Программа численного интегрирования уравнения движения (случай финитного движения).
|
|
Рис. 5.9. Фазовая диаграмма и зависимость от времени координаты частицы, совершающей финитное движение в потенциальной яме.
|
|
Рис. 5.11. Фазовая диаграмма и зависимость от времени координаты частицы, совершающей инфинитное движение в потенциальной яме.
Вопросы и задачи для самостоятельной работы
Решить задачу о зависимости от времени координаты тела, движущегося пол действием силы вязкого трения, величина которой зависит от скорости по квадратичному закону:
![]()
Построить графики зависимости от времени координаты, скорости и ускорения тела, падающего с вязкой среде.
Решить задачу об одномерном движении тела под действием упругих сил в случае произвольных начальных условий (v00, x00 ). Попытайтесь получить графики зависимости от времени координаты и скорости частицы при различных начальных условий, решая дифференциальное уравнение движения при помощи какого-либо стандартного математического пакета.
Исследовать движение частицы под действием упругих сил при наличии вязкого трения. Какие принципиально различные формы движения могут существовать в этом случае?
*Основываясь на полученных в п.5.4 результатах постройте примерные графики зависимостей натяжения нити от времени и угловой скорости от угла отклонения («фазовую траекторию» нелинейного маятника) в четырех рассмотренных на лекции предельных случаях. Проверьте правильность своих рассуждений на компьютерных моделях.
** Рассмотрите одномерное движение частицы в поле сил, потенциальная энергия которых имеет вид, изображенный на рис.:

При анализе каких систем может оказаться полезным полученные вами решения?