Пирогов. Сопротивление материалов 2008

Решение. Очевидно, что в опорах А и D под действием приложенной нагрузки возникают реактивные моменты МА и МD. Из уравнений статики можем записать лишь одно – уравнение моментов относительно оси х. Таким образом, число неизвестных превышает число возможных уравнений статики, т.е. система обладает первой степенью статической неопределимости.

Выбираем эквивалентную статически определимую систему. Для этого связь, налагаемую заделкой А, препятствующую повороту сечения А, отбрасываем и заменяем моментом МА, приложенным по предполагаемому направлению его действия (рис. 32, б). Используя принцип независимости действия силовых факторов, представим угол поворота сечения А в следующем виде:

ϕA (M A, m1, m2 ) = ϕA (M A ) + ϕA (m1) + ϕA (m2 ) .

Каждое из трех слагаемых представляет поворот сечения А под действием соответствующего крутящего момента. Сечение А неподвижно и, следовательно,

ϕA (M A ) + ϕA (m1 ) + ϕA (m2 ) = 0 .

Поворот сечения А под действием момента МА равен:

Первое слагаемое в выражении (6.22) представляет поворот сечения А относительно В согласно (6.13).

Второе слагаемое – поворот сечения В относительно сечения D.

Суммируем (6.22), (6.23) и (6.24) и учтем, что m1 = т, а m2 = 2т.

Получаем:

Полярный момент инерции сечения на участке AB (J pAB ) согласно (6.9) равен:

равны:

J pBD = J CDp = 32π D4 .

Подставляя J pAB , J pBD , J CDp в уравнение (6.25), получаем:

2M A +3M A +3m −4m = 0 ,

или M A = 0,2m.

Ответ получен со знаком «плюс», что подтверждает предположение о направлении действия момента M A .

Построение эпюры крутящих моментов M x . Мысленно рас-

секая вал на участках АВ, ВС и CD, отбрасывая каждый раз левую часть и используя метод приведения (правило для определения внутреннего силового фактора M x ), находим:

участок АВ: M x = M A = 0,2m;

участок ВС: M x = M A + m1 = 0,2m + m =1,2m;

участок CD: M x = M A + m1 − m2 = 0,2m + m − 2m = −0,8m.

Эпюра M x представлена на рис. 32, в.

Построение эпюры углов поворота. Крутящие моменты в пре-

делах участков АВ, ВС и CD постоянны. Следовательно, согласно (6.13) имеем линейную зависимость φ(x).

62

сечения В относительно неподвижного сечения А. На участке ВС:

Эпюра φ(x) представлена на рис. 32, г.

Расчет на прочность. Участок ВС опаснее участка CD, так как

M xBC > M xCD .

На участках АВ и ВС вал обладает различным полярным моментом сопротивления. Поэтому сравним максимальные касательные напряжения на этих участках.

D ≥ 3 25,48 10−6 ≈ 2,94 10−2 м = 2,94 cм.

Расчет на жесткость. Из эпюры φ(x) видно, что наибольший угол относительного закручивания (θmax) на участке ВС.

Принимаем

D = 6 см.

Из двух найденных значений для D выбираем большее, поэтому

D = 6 см.

64

6.5. Брус прямоугольного поперечного сечения

Задача об определении напряжений и деформаций в брусе некруглого сечения не может быть решена методами СМ. Здесь гипотеза плоских сечений неприемлема. Как показывает опыт, при кручении бруса прямоугольного профиля поперечные сечения бруса искривляются. Для точного решения задачи необходимо гипотезу плоских сечений заменить в данном случае условием неразрывности деформаций, что приводит к значительному усложнению решения. Однако некоторые соображения относительно законов распределения напряжений в поперечных сечениях некруглой формы могут быть высказаны.

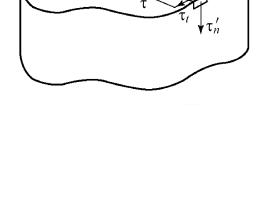
Прежде всего, можно установить, что касательные напряжения в точках контура поперечного сечения должны быть направлены по касательной к контуру. Действительно, положим, что в точке А (рис. 33) касательное напряжение τ будет направлено под некоторым углом к контуру. Тогда оно может быть разложено на две составляющие: по касательной к контуру (τt ) и по нормале (τn ) . По

закону парности касательных напряжений на поверхности вала должно возникнуть касательное напряжение τ′n = τn . Но по-

верхность свободна от нагрузки и, следовательно, τ′n , а с ней и τn должны быть равны нулю.

Рис. 33

65

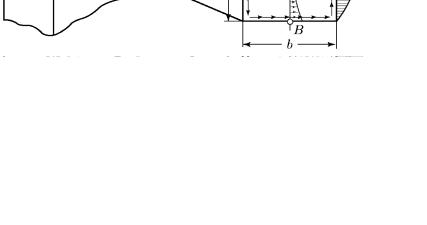
Аналогично рассуждая, можно показать, что в углах прямоугольного поперечного сечения касательные напряжения равны нулю. Если допустить, что в угловой точке (рис. 34) возникло напряжение τ, то его можно разложить на две составляющие τ1 и τ2 ,

направленные по сторонам прямоугольника. В этом случае по закону парности касательных напряжений получим на свободных поверхностях вала напряжения τ1′ и τ′2 , что противоречит услови-

ям нагружения. Следовательно, в угловых точках прямоугольного поперечного сечения бруса касательные напряжения отсутствуют.

Рис. 34 Рис. 35

На рис. 35 показана эпюра касательных напряжений, полученная методами теории упругости для бруса прямоугольного поперечного сечения. В его углах напряжения равны нулю, а наибольшие напряжения возникают в точках А, лежащих в серединах

сательные напряжения посередине коротких сторон (точки В) равны:

66

Формулы (6.26) и (6.28) могут рассматриваться как обобщающие. В случае круглого поперечного сечения Jк = J p , a Wк =Wp .

67

где a1, a2 , ..., a5 – расстояния от линии действия силы, отмечен-

ной соответствующим индексом, до оси z.

Мысленно отбросим часть балки справа от проведенного сечения и рассмотрим условие равновесия левой части (рис. 36, б). Видно, что действующие силы на оставшуюся часть балки не уравновешены. Следовательно, в поперечном сечении возникает поперечная сила Qy . Делаем предположение, что она направлена так

же, как и сила P5 , что вполне очевидно в нашем случае. Тогда ее

величина определится из первого уравнения равновесия для оставшейся части балки:

P1 + P2 = P3 + P4 +Qy .

Учитывая уравнение (7.1), находим, что

Qy = P5 .

Получили ответ со знаком «плюс», что свидетельствует о верности предположения о направлении действия силы Qy . Если бы из-

начально направили силу Qy в противоположном направлении, ре-

зультат получился бы со знаком «минус».

Для равновесия левой части балки необходимо, чтобы и сумма моментов от сил, приложенных к этой части относительно оси z, была равна нулю. Видно, что последнее условие будет удовлетворено, если предположить наличие в поперечном сечении внутреннего силового фактора – изгибающего момента M z , направленного

так же, как и момент от силы P5 .

В этом случае второе уравнение равновесия записывается в виде:

P1a1 + P2a2 − P3a3 − P4a4 + M z = 0 .

Учитывая уравнение (7.2), находим, что

M z = P5a5 .

69

И здесь получаем результат со знаком «плюс», что подтверждает предположение о направлении действия M z .

Перенесем секущую плоскость вместе с координатными осями y – z так, чтобы она проходила между линиями действия сил P2 и

P4 (рис. 36, в).

Расстояния от линий действия сил до новой оси z станут равны a1′, a′2 , ..., a5′ . Уравнение равновесия балки (7.1) сохраняется, а

уравнение (7.2) примет вид:

Сила P2 теперь находится справа от новой оси z и создает отри-

цательный момент. Если отбросить часть балки справа от сечения, то условие равновесия оставшейся части выразится уравнениями:

P1 = P3 + P4 +Qy ,

P1a1′ − P3a3′ − P4a4′ + M z = 0 .

Учитывая уравнения (7.1) и (7.3), находим

Qy = P5 − P2 ,

M z = P5a5′ − P2a′2 .

Обобщая полученные результаты, можно сформулировать правила для определения Qy и M z в поперечных сечениях балки при

изгибе.

Поперечная сила Qy равна сумме проекций на ось у в плоскости

сечения всех внешних сил, взятых с одной стороны от сечения. Изгибающий момент M z равен сумме моментов относительно

оси z всех сил, взятых с одной стороны от сечения.

Сформулированные правила выражают так называемый метод приведения. Все силы, действующие на отброшенную часть, переносим в рассматриваемое сечение, сохраняя их величины и направление.

Таким образом, поперечная сила Qy является равнодействую-

щей всех перенесенных сил. При переносе сил в новое сечение добавляем момент, который производит эта сила относительно оси z в этом сечении. Эти операции находятся в полном соответствии с

70